WikiDer > Род Эйлера – Фоккера - Википедия

В теория музыки и настройка, Род Эйлера – Фоккера (множественное число: роды), названный в честь Леонард Эйлер и Адриан Фоккер,[1] это музыкальная гамма в просто интонация высота звука которого может быть выражена как товары некоторых из членов некоторых мультимножество создания основной факторы. Степень двойки обычно игнорируется из-за того, как человеческое ухо воспринимает октавы как эквивалент.
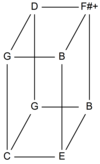
Х-мерное измерение тона содержит х факторов. «Род Эйлера-Фоккера с двумя измерениями может быть представлен в двумерной (прямоугольной) тоновой сетке, один с тремя измерениями в трехмерной (блочной) тоновой решетке. Роды Эйлера-Фоккера характеризуются перечисление количества шагов в каждом измерении. Количество шагов представлено многократным упоминанием измерения, поэтому возникают такие описания, как [3 3 5 5], [3 5 7], [3 3 5 5 7 7 11 11] и т. Д. "[1] Например, мультимножество {3, 3, 7} дает род Эйлера – Фоккера [3, 3, 7], который содержит следующие шаги:
1 3 =3 7=7 3×3 =9 3×7=21 3×3×7=63
Нормализованные до октавы, они становятся: 1/1, 9/8, 21/16, 3/2, 7/4, 63/32. ![]() Играть в (помощь·Информация)
Играть в (помощь·Информация)
Роды Эйлера образуются из простых множителей 3 и 5, тогда как род Эйлера – Фоккера может иметь множители 7 или любое большее простое число. В степень - количество интервалов, порождающих род. Однако не все роды одной степени имеют одинаковое количество тонов, поскольку [XXXYYY] также может быть обозначен как [XИксYу], «степень, таким образом, является суммой показателей», и количество шагов получается добавлением единицы к каждой экспоненте, а затем их умножением ((X + 1) × (Y + 1) = Z).[2]
Адриан Фоккер написал большую часть своей музыки в жанрах Эйлера-Фоккера, выраженных в 31-тональный ровный темперамент. Алан Ридаут также использовали роды Эйлера-Фоккера.[2]
Полный сокращенный аккорд
Род Эйлера – Фоккера также можно назвать полный сокращенный аккорд. Эйлер ввел термин полный аккорд, в то время как Фоккер ввел весь термин.[2]
Полный аккорд состоит из двух высот: основного тона и основного тона, причем направляющий тон кратен основному. Между ними находятся другие высоты, которые можно рассматривать как кратные фундаментальный или как делители направляющий тон (отональность и утональность). Например, если взять 1 в качестве основного и выбрать 15 в качестве направляющего тона, получим: 1: 3: 5: 15 (род [35]). Отношение основного тона к основному - это «число натяжения» или «экспоненсы» (Эйлер: Exponens consonantiae).[2]
Список родов Эйлера
| Вторая степень | ||||||
|---|---|---|---|---|---|---|
| Роды | Примечания | |||||
| 33 | 1/1 | 9/8 | 3/2 | |||
| 35 | 1/1 | 5/4 | 3/2 | 15/8 | ||
| 55 | 1/1 | 5/4 | 25/16 | |||
| Третья степень | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Роды | Примечания | |||||||||
| 333 | 1/1 | 9/8 | 3/2 | 27/16 | ||||||
| 335 | 1/1 | 9/8 | 5/4 | 45/32 | 3/2 | 15/8 | ||||
| 355 | 1/1 | 75/64 | 5/4 | 3/2 | 25/16 | 15/8 | ||||
| 555 | 1/1 | 5/4 | 25/16 | 125/64 | ||||||
| Четвертая степень | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Роды | Примечания | ||||||||||||||
| 3333 | 1/1 | 9/8 | 81/64 | 3/2 | 27/16 | ||||||||||
| 3335 | 1/1 | 135/128 | 9/8 | 5/4 | 45/32 | 3/2 | 27/16 | 15/8 | |||||||
| 3355 | 1/1 | 9/8 | 75/64 | 5/4 | 45/32 | 3/2 | 25/16 | 27/16 | 225/128 | 15/8 | |||||
| 3555 | 1/1 | 75/64 | 5/4 | 375/256 | 3/2 | 25/16 | 15/8 | 125/64 | |||||||
| 5555 | 1/1 | 625/512 | 5/4 | 25/16 | 125/64 | ||||||||||
...
Смотрите также
Источники
- ^ а б Раш, Рудольф (2000). Гарри Партч, стр.31-2. Данн, Дэвид, изд. ISBN 978-90-5755-065-2.
- ^ а б c d "Что такое род Эйлера – Фоккера?", Huygens-Fokker.org.
дальнейшее чтение
- фр: Франк Енжеевски (2006). Математическая теория музыки, п. 157. ISBN 978-2-7521-0023-8.