WikiDer > Срединный темперамент
Срединный темперамент это музыкальный темперамент, это система настройки, полученный путем небольшого компромисса пятых с целью улучшения третей. Температуры срединного тона строятся так же, как и Пифагорейский тюнинг, как стопка из равных пятых, но значит, каждая пятая часть узкий по сравнению с идеальный пятый соотношения 3: 2.
Выражено в терминах парадигмы динамической тональности
Используя терминологию и концепции Динамическая тональность парадигме, средний темперамент определяется как синтонический темперамент с диапазоном настройки от P5 = 694,79 до P5 = 701,96 ". Это ограничение является артефактом Парадигма статических тембров, которая была доминирующей парадигмой, особенно для клавишных инструментов, вплоть до наших дней. В парадигме статических тембров ноты стройки смягчаются от Just Intonation, но частичные тембры не смягчаются от гармонической серии.
Темперирование нот настройки, но не частей тембров, в которых эта настройка воспроизводится, неизбежно приводит к несовпадению нот и частей, таким образом делая настройку и тембр менее «связанными».[1] Чем меньше связаны строй и тембр, тем менее созвучны они при совместной игре. Это смещение ограничивалось диапазоном настроек, которые были созвучны при игре с использованием гармонических тембров.
Поскольку темперамент meanone является поддиапазоном синтонической темперации, которая является темпераментом ранга 2, в этой статье кратко обсуждаются темпераменты ранга 2 и синтоническая темперамент.
Ранг-2 темпераменты
в Динамическая тональность парадигма, данный темперамент ранга 2 определяется периодом α, генератором β и последовательность запятых.[2] Темперамент ранга 2 определяет ранг 2 (т.е., двумерный) note-space, как показано в Видео 1.
Синтонический темперамент
Синтонический темперамент - это темперамент второго ранга, определяемый периодом (идеальная октава, 1/2), генератором (идеальная квинта, 3/2) и последовательностью запятой (которая начинается с синтоническая запятая, 81/80, который называет темперамент). Построение нотного пространства синтонной темперации показано в Видео 2.
Допустимый диапазон настройки синтонической темперации показан на рисунке 1 как простирающийся от P5 = 686 ¢ до P5 = 720 ¢, диапазон (720-686 =) 34.
Средний темперамент
Темперамент meanone точно такой же, как и у синтонической: то есть у них одинаковый период (октава), генератор (идеальная квинта) и последовательность запятых (начиная с синтонической запятой). Единственное отличие состоит в том, что диапазон настройки средней темперации ограничивается поддиапазоном допустимого диапазона настройки синтонической темперации, эквивалентным «диапазону настройки Purer».[3] показано на рисунке 1 (слева, зеленым цветом), от P5 = 694,79 (что дает только второстепенные трети) до P5 = 701,96 ¢ (что дает только идеальные квинты), диапазон настройки всего (701,96-694,79 =) 7,17 ¢.

Почему имеется в виду более узкий диапазон настройки?
Тембральные части тембра так, чтобы они совпадали с нотами настройки в соответствии с Динамическая тональность, максимизирует созвучие во всем диапазоне настройки синтонной темперации.
Более узкий диапазон среднего темперамента - это артефакт Парадигма статических тембров, в котором просто настроены псевдо-справедливость, но Гармоничные тембры в которых играются эти строчки, нетронутые. Это неизбежно приводит к смещению нот настройки и частичных тембров, делая их менее связанными.[1] и, следовательно, менее согласный. Чем дальше вы настраиваетесь от определенного поддиапазона настройки определенной темперации, тем менее связанными будут настройка и тембр, и, следовательно, тем менее согласным будет использование незатемненных гармонических тембров.
Вне этого раздела в этой статье обсуждается темперамент meanone в первую очередь в контексте парадигмы статического тембра.
Известные средние темпераменты
Равный темперамент, полученный путем создания всех полутонов одинакового размера, каждый равный одной двенадцатой октавы (с отношением корня 12-й степени из 2 к единице (12√2: 1), сужает пятую часть примерно на 2 цента или 1/12 Пифагорейская запятая, и производит трети, которые лишь немного лучше, чем при настройке Пифагора. Равный темперамент примерно такой же, как 1/11 запятая означает одну настройку.
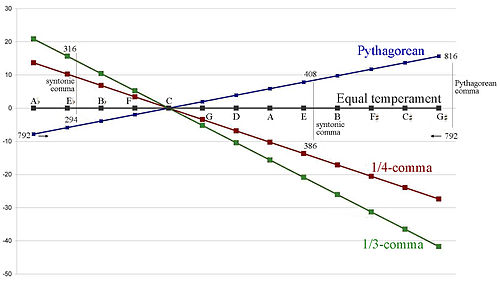
Четверть запятой означает один, который смягчает пятую часть 1/4 запятой, является наиболее известным типом темперамента среднего и одного человека, а термин имел в виду один темперамент часто используется для обозначения именно этого. Четыре восходящих квинта (как C – G – D – A – E), умеренные 1/4 запятой, создают идеальный большая треть (C – E), один синтоническая запятая уже, чем пифагорейская треть, полученная в результате четырех идеальные квинты. Четверть-запятая означала, что это практиковалось с начала 16 века до конца 19 века.
В случае третьей запятой, означающей один, квинты смягчаются 1/3 запятой, а три убывающих квинта (например, A – D – G – C) дают идеальную минорную треть (A – C). синтоническая запятая шире пифагорейского, который возник бы в результате трех идеальные квинты. Третья запятая означает, что один может быть приблизительно равен делению октавы в 19 равных шагов.
Тон как средство
Название «означало один темперамент» происходит от того факта, что все такие темпераменты имеют только один размер тона, в то время как просто интонация производит основной тон и второстепенный, отличающийся синтоническая запятая. В любой обычной системе (т.е. со всеми пятыми, кроме одной одинакового размера)[5] тон (как C – D) достигается после двух пятых (как C – G – D), в то время как мажорная треть достигается после четырех пятых: таким образом, тон составляет ровно половину мажорной трети. В этом смысле тон является средним.
В случае четверти запятой означает один, кроме того, когда большая треть сужается синтонической запятой, тон также на половину запятой уже, чем основной тон только интонации, или на половину запятой шире, чем второстепенный тон: это еще один смысл, в котором тон в четверть тона темперамента может считаться средним тоном, и это объясняет, почему четверть запятая, означающая один, часто считается, собственно, средним темпераментом.[6]
Срединный темперамент
«Срединный» может иметь следующие эквивалентные определения:
- Среднее значение - это среднее геометрическое между основным целым тоном (9: 8 в простой интонации) и второстепенным целым тоном (10: 9 в простой интонации).
- Среднее значение - это среднее значение его основной трети (например, квадратный корень из 5: 4 в четверть запятой означает один).
Семейство темпераментов означает один общий характер, что они образуют стопку идентичных квинт, тон является результатом двух квинт минус одна октава, большая треть из четырех пятых минус две октавы. Температуры средних тонов часто описываются долей синтонической запятой, с помощью которой смягчаются квинты: четверть запятой означает один, наиболее распространенный тип, смягчает пятую часть1⁄4 синтонической запятой, в результате чего четыре пятых образуют только мажорную треть, синтоническую запятую ниже мажорной трети Пифагора; третья запятая означала, что1⁄3 синтонической запятой, три пятых дают только мажорную шестую, синтоническая запятая ниже пифагорейской.
Средний темперамент - это линейный темперамент,[2]:15-32 отличается шириной своего генератор (часто измеряется в центы), как показано в центральном столбце рисунка 1. Исторически известные темпераменты означающих, обсуждаемые ниже, занимают узкую часть этого континуума настройки, с пятыми в диапазоне приблизительно от 695 до 699 центов.
Хотя срок имел в виду один темперамент относится в первую очередь к закалке 5-предел музыкальные интервалы, темпераменты, которые хорошо аппроксимируют 5-предельные интервалы, например Четверть запятой означает один, может также приблизить 7-предел интервалы хорошо, определяя семеричный означаетодин темперамент. На рисунке 1 показаны допустимые диапазоны настройки для 5-предельных, 7-предельных и 11-предельных настроек, и, как можно видеть, они включают в себя многие известные настройки Meanone.[требуется разъяснение].
Температуры средних тонов могут быть заданы различными способами: какой долей (логарифмически) синтонической запятой сглаживается пятая часть (как указано выше), какая равный темперамент имеет значение одна квинта, о которой идет речь, ширина темперированной совершенной квинты в центах или отношение всего тона к диатоническому полутон. Это последнее соотношение было названо "р"американского композитора, пианиста и теоретика Исли Блэквуд, но на самом деле использовался гораздо дольше. Это полезно, потому что дает нам представление о мелодических качествах настройки, и потому, что если р это рациональное число N/D, так это 3р + 1/5р + 2 или 3N + D/5N + 2D, что составляет пятую по величине логарифмы база 2, которая сразу сообщает нам, какое деление октавы у нас будет. Если мы умножим на 1200, мы получим пятую часть в центах.
В этих терминах некоторые исторически известные настройки Meanone перечислены ниже. Второй и четвертый столбцы соответствуют приближениям к первому столбцу. Третий столбец показывает, насколько близка аппроксимация второго столбца к фактическому размеру пятого интервала в данной настройке среднего значения из первого столбца.
| Доля (синтонической) запятой | Чистый интервал | Примерный размер пятой части в октавах | Ошибка (в центах) | Соотношение р |
|---|---|---|---|---|
| 1⁄315 (почти пифагорейская настройка) | 3311×5⁄2495 (но3⁄2 можно считать чистым для всех практических целей) | 31⁄53 | +6.55227×10−5 | 9:4 |
| 1⁄11 (1⁄12 Пифагорейская запятая) | 16384⁄10935 (214⁄37×5) (Пятый Кирнбергер (просто идеальный пятый, сглаженный раскол)) | 7⁄12 | +1.16371×10−4 | 2:1 |
| 1⁄6 | 45⁄32 и64⁄45 | 32⁄55 | -1.88801×10−1 | 9:5 |
| 1⁄5 | 15⁄8 и16⁄15 | 25⁄43 | +2.06757×10−2 | 7:4 |
| 1⁄4 | 5⁄4 и8⁄5 | 18⁄31 | +1.95765×10−1 | 5:3 |
| 2⁄7 | 25⁄24 и48⁄25 | 29⁄50 | +1.89653×10−1 | 8:5 |
| 1⁄3 | 5⁄3 и6⁄5 | 11⁄19 | -4.93956×10−2 | 3:2 |
| 1⁄2 | 9⁄5 и10⁄9 | 15⁄26 | +1.10584×100 | 4:3 |
Равные темпераменты
Ни пятая часть, ни четверть запятой не означают, что одна пятая рациональный доля октавы, но существует несколько настроек, приближающих квинту таким интервалом; это подмножество равные темпераменты ("N-ET "), в котором октава делится на некоторое число (N) одинаково широких интервалов.
Равные темпераменты, которые можно использовать в качестве одной из настроек, включают (в порядке возрастания генератор ширина) 19-ET, 50-ET, 31-ET, 43-ET и 55-ET. Чем дальше настройка удаляется от четверти запятой, означающей, тем не менее[1] настройка на гармонические тембры, которые можно преодолеть закалять частички чтобы соответствовать настройке - но это возможно только на электронных синтезаторах.[7]
| C | C♯ | D♭ | D | D♯ | E♭ | E | E♯ | F | F♯ | г♭ | г | г♯ | А♭ | А | А♯ | B♭ | B | C♭ | C | |
| 1/4 запятой: | 0.00 | 76.05 | 117.11 | 193.16 | 269.21 | 310.26 | 386.31 | 462.36 | 503.42 | 579.47 | 620.53 | 696.58 | 772.63 | 813.69 | 889.74 | 965.78 | 1006.84 | 1082.89 | 1123.95 | 1200.00 |
| 31-ЕТ: | 0.00 | 77.42 | 116.13 | 193.55 | 270.97 | 309.68 | 387.10 | 464.52 | 503.23 | 580.65 | 619.35 | 696.77 | 774.19 | 812.90 | 890.32 | 967.74 | 1006.45 | 1083.87 | 1122.58 | 1200.00 |
Интервалы волка
Целое число идеальных квинт никогда не даст в сумме целого числа октав, потому что они несоизмеримы (см. Основная теорема арифметики). Если сложенное целое количество идеальных квинт слишком близко к октаве, тогда один из интервалов, который энгармонически эквивалентен квинте, должен иметь другую ширину, чем другие квинты. Например, чтобы сделать 12-нотную хроматическую гамму в Пифагорейский тюнинг закрыть на октаву, один из пятых интервалов должен быть понижен ("расстроен") на Пифагорейская запятая; эта измененная пятая часть называется волк пятый потому что по размеру интервала он похож на квинтэссен и кажется расстроенным квинтом. Однако на самом деле это пифагорейская уменьшенная шестая (или увеличенная треть вместо четвертой), скажем, интервал между C и E♯.
Интервалы волка - это артефакт дизайна клавиатуры.[8] Проще всего это показать, используя изоморфную клавиатуру, как показано на рисунке 2.
На изоморфная клавиатура, любой музыкальный интервал имеет одинаковую форму, где бы он ни появлялся, кроме краев. Вот пример. На клавиатуре, показанной на рисунке 2, от любой данной ноты нота, которая на одну квинт выше, всегда находится рядом с данной нотой вверх и вправо. В диапазоне нот этой клавиатуры нет волчьих интервалов. Проблема на краю, на ноте E♯. Нота, которая на идеальную пятую часть выше, чем E♯ это б♯, которого нет на показанной клавиатуре (хотя его можно было бы включить в большую клавиатуру, расположенную справа от A♯, следовательно, поддерживая последовательный нотный рисунок клавиатуры). Потому что нет B♯ кнопка, когда играет E♯ силовой аккорд, нужно выбрать другую ноту, например C, чтобы играть вместо отсутствующей B♯.
Даже граничные условия создают волчьи интервалы только в том случае, если изоморфная клавиатура имеет меньше кнопок на октаву, чем имеет настройка. энгармонично-четкие ноты (Milne, 2007). Например, изоморфная клавиатура на рисунке 2 имеет 19 кнопок на октаву, поэтому упомянутое выше краевое условие из E♯ к C, является не интервал волков в 12-ET, 17-ET или 19-ET; однако это является интервал волков 26-ET, 31-ET и 50-ET. В этих последних настройках с помощью электронного транспонирования можно было сохранить ноты текущей клавиши на белых кнопках изоморфной клавиатуры, так что эти волчьи интервалы очень редко встречаются в тональной музыке, несмотря на модуляцию на экзотические клавиши.[9]
Изоморфные клавиатуры демонстрируют инвариантные свойства настроенных синтонический темперамент изоморфно (то есть, например, выставляя заданный интервал с единой согласованной формой между кнопками в каждой октаве, тональности и настройке), потому что и изоморфная клавиатура, и темперамент двумерны (т.е., ранг-2) сущностей (Милн, 2007). Одномерный N-клавиатуры могут точно отображать инвариантные свойства только одного одномерного N-ЭТ тюнинг; следовательно, одномерная клавиатура в стиле фортепиано с 12 клавишами на октаву может раскрыть инвариантные свойства только одной настройки: 12-ET.
Когда идеальная пятая - ровно 700 центы широкий (то есть закаленный приблизительно1⁄11 синтонической запятой, или точно1⁄12 запятой Пифагора) то настройка идентична знакомой 12-тональной равный темперамент. Это отображается в таблице выше, когда р = 2:1.
Из-за компромиссов (и волчьих интервалов), навязанных однозначным настройкам одномерной фортепианной клавиатуры, хорошие темпераменты и со временем равный темперамент стал более популярным.
Используя стандартные названия интервалов, двенадцать пятых равны шести октавам плюс одна расширенный седьмой; семь октав равны одиннадцати пятым плюс одна уменьшился шестой. Учитывая это, на самом деле три «второстепенных трети» увеличенные секунды (например, B♭ в C♯), а четыре "основные трети" на самом деле уменьшенные четверти (например, от B до E♭). Несколько триад (например, B – E♭–F♯ и B♭–C♯–F) содержат оба этих интервала и имеют нормальные квинты.
Расширенные средства
Все настройки означающие попадают в допустимый диапазон настройки синтонический темперамент, поэтому все настройки Meanone являются синтоническими. Все синтонические строчки, включая средние тона, имеют концептуально бесконечное количество нот в каждой октаве, то есть семь естественных нот, семь острых нот (F♯ в B♯), семь плоских нот (B♭ к F♭), двойные диезы, двойные диезы, тройные диезы и бемоль и т. д. На самом деле двойные диезы и бемоль редко, но все же необходимы; тройной диез и бемоль практически не встречается. В любой синтонической настройке, которая разделяет октаву на небольшое количество равных по ширине наименьших интервалов (например, 12, 19, или 31), эта бесконечность нот все еще существует, хотя некоторые ноты будут эквивалентными. Например, в 19-ET, E♯ и F♭ одинаковая подача.
Многие музыкальные инструменты способны очень тонко различать высоту звука, например, человеческий голос, тромбон, струны без натяжения, такие как скрипка, и лютни со связанными ладами. Эти инструменты хорошо подходят для использования строев соло.
С другой стороны, фортепианная клавиатура имеет только двенадцать физических устройств управления нотами на октаву, что делает ее плохо подходящей для любых других строев, кроме 12-ET. Почти все исторические проблемы с темпераментом meanone вызваны попыткой сопоставить бесконечное количество нот на октаву meanone с конечным числом клавиш фортепиано. Это, например, источник обсуждаемого выше «волчьего пятого». При выборе нот для сопоставления с черными клавишами фортепиано удобно выбирать те ноты, которые являются общими для небольшого числа тесно связанных клавиш, но это будет работать только до края октавы; при переходе к следующей октаве нужно использовать «волчью пятую», которая не такая широкая, как другие, как обсуждалось выше.
Существование «волчьей пятой» является одной из причин того, что до введения хороший темперамент, инструментальная музыка обычно оставалась в нескольких «безопасных» тональностях, которые не включали «волчью пятую» (которая обычно помещалась между G♯ и E♭).
На протяжении эпохи Возрождения и Просвещения теоретики были самыми разными. Никола Вичентино, Франсиско де Салинас, Фабио Колонна, Марин Мерсенн, Кристиан Гюйгенс, и Исаак Ньютон выступал за использование настроек Meanone, выходящих за пределы двенадцати нот клавиатуры,[10][11][12] и, следовательно, стали называться "расширенными" означенными настройками. Эти усилия потребовали сопутствующего расширения клавишных инструментов, чтобы предложить средства управления более чем 12 нот на октаву, включая Archicembalo Винсенто (показано на рисунке 3), клавесин Мерсенна 19-ET, самбуку 31-ET Колонны и клавесин 31-ET Гюйгенса .[13] Другие инструменты расширили клавиатуру всего на несколько нот. Некоторые клавесины и органы того времени разделили D♯/ E♭ ключи, так что оба Ми мажор/C♯ незначительный (4 острых предмета) и E♭ главный/До минор (3 квартиры) можно играть без волчьих пятерок. Многие из этих инструментов также имеют разделение G♯/ А♭ ключей, а в некоторых из них все пять случайных ключей разделены.
Все эти альтернативные инструменты были «сложными» и «громоздкими» (Isacoff, 2003) из-за (а) не изоморфности и (б) отсутствия возможности электронного транспонирования, что может значительно сократить количество контролирующих ноты. кнопки, необходимые на изоморфная клавиатура (Пламондон, 2009). Обе эти критические замечания могут быть устранены с помощью электронных изоморфных клавишных инструментов (таких как оборудование с открытым исходным кодом подавитель клавиатуры), которые могут быть проще, менее громоздкими и выразительными, чем существующие клавишные инструменты.[14]
Использование среднего темперамента
Ссылки на системы настройки, которые могли относиться к meanone, были опубликованы еще в 1496 году (Gafori), а Aron (1523) безошибочно имеет в виду meanone. Тем не менее, первые математически точные описания настройки Meantone можно найти в трактатах конца 16 века автора Франсиско де Салинас и Джозеффо Зарлино. Салинас (в De musica libra septem, 1577) описывает три различных темперамента среднего тона: систему третьей запятой, систему двух седьмых запятых и систему четверти запятой. Он является вероятным изобретателем системы третьей запятой, в то время как он и Зарлино оба писали по системе две-седьмой запятой, очевидно независимо. Лодовико Фольяно упоминает систему с четвертью запятой, но не обсуждает ее.
В прошлом темпераменты, обозначающие один, иногда использовались или упоминались под другими названиями или описаниями. Например, в 1691 г. Кристиан Гюйгенс написал его "Lettre touch le cycle harmony" («Письмо о гармоническом цикле») с целью введения того, что он считал новым делением октавы. В этом письме Гюйгенс несколько раз сравнительно ссылался на обычную настройку, которую он обозначал по-разному как «обыкновенный темперамент» или «тот, который все используют». Но описание Гюйгенсом этого условного устройства было довольно точным и явно идентифицируемо с тем, что теперь классифицируется как (четверть запятой) имел в виду один темперамент.[15]
Хотя meanone больше всего известен как среда настройки, связанная с более ранней музыкой эпохи Возрождения и барокко, есть свидетельства непрерывного использования Meanone в качестве клавишной темперации вплоть до середины XIX века.[16] Темперамент срединного тона значительно возродился в исполнении старинной музыки в конце 20-го века и во вновь созданных произведениях, особенно требующих внимания композиторов, включая Джон Адамс, Дьёрдь Лигети и Дуглас Лиди.
Смотрите также
- Динамическая тональность
- Равный темперамент
- Просто интонация
- Интервал
- Математика музыкальных гамм
- Пифагорейский тюнинг
- Полутон
- Хороший темперамент
- Обычный темперамент
- Список подразумеваемых интервалов
использованная литература
- ^ а б c Сетхарес, Уильям (Сентябрь 1993 г.). «Местное созвучие и соотношение тембра и гаммы». Журнал Акустического общества Америки. 94 (3): 1218–1228. Дои:10.1121/1.408175.
- ^ а б Milne, A .; Sethares, W.A .; Пламондон, Дж. (Зима 2007 г.). «Инвариантные пальцы в настраиваемом континууме». Компьютерный музыкальный журнал. 31 (4): 15–32. Дои:10.1162 / comj.2007.31.4.15. S2CID 27906745. Альтернативный URL
- ^ Milne, A .; Sethares, W .; Пламондон, Дж. (2006). "Система X" (PDF). Технический отчет, Thumtronics Inc.. Получено 2020-05-02.
- ^ Пламондон, Джим; Милн, Эндрю Дж .; Сетхарес, Уильям (2009). Динамическая тональность: расширение тональности в 21 век (PDF). Труды Ежегодной конференции Южного центрального отделения Музыкального общества колледжа.
- ^ Дж. Мюррей Барбур, Тюнинг и темперамент. Исторический обзор. Ист-Лансинг, 1951, стр. xi.
- ^ Барбур 1951, стр. x и стр. 25-44.
- ^ Сетхарес, Уильям; Milne, A .; Tiedje, S .; Prechtl, A .; Пламондон, Дж. (2009). «Спектральные инструменты для динамической тональности и морфинга звука». Компьютерный музыкальный журнал. 33 (2): 71–84. CiteSeerX 10.1.1.159.838. Дои:10.1162 / comj.2009.33.2.71. S2CID 216636537. Получено 2009-09-20.
- ^ Милн, Эндрю; Sethares, W.A .; Пламондон, Дж. (Март 2008 г.). «Настройка Continua и раскладки клавиатуры». Журнал математики и музыки. 2 (1): 1–19. CiteSeerX 10.1.1.158.6927. Дои:10.1080/17459730701828677. S2CID 1549755.
- ^ Пламондон, Джим; Milne, A .; Сетхарес, W.A. (2009). «Динамическая тональность: расширение тональности в 21 век» (PDF). Материалы ежегодной конференции Южно-центрального отделения Музыкального общества колледжа.
- ^ Барбур, Дж. М., 2004 г., Тюнинг и темперамент: исторический обзор.
- ^ Даффин Р.В., 2006 г., Как равный темперамент разрушил гармонию (и почему вам это должно быть небезразлично).
- ^ Исакофф, Стюарт, 2003, Темперамент: как музыка стала полем битвы великих умов западной цивилизации
- ^ Стембридж, Кристофер (1993). "Cimbalo Cromatico и другие итальянские клавишные инструменты с девятнадцатью или более делениями на октаву". Обзор практики производительности. vi (1): 33–59. Дои:10.5642 / perfpr.199306.01.02.
- ^ Paine, G .; Стивенсон, I .; Пирс, А. (2007). "Проект картографирования Thummer (ThuMP)" (PDF). Труды 7-й Международной конференции по новым интерфейсам для музыкального выражения (NIME07): 70–77.
- ^ (См. Ссылки, указанные в статье 'Обычный темперамент'.)
- ^ Джордж Гроув писал еще в 1890 году: «Режим настройки, который преобладал до введения равного темперамента, называется системой Meantone. В Англии он еще не умер, поскольку его все еще можно услышать на некоторых органах в деревенских церквях. По словам Дона Б. Иньигеса, органиста Севильского кафедрального собора, система средних единиц обычно сохраняется на испанских органах даже в наши дни ». Словарь музыки и музыкантов, Macmillan, Лондон, т. IV, 1890 [1-е издание], с. 72.
внешние ссылки
- Объяснение построения Quarter Comma Meantone Tuning
- LucyTuning - конкретное означает одно, производное от числа Пи, и сочинения Джона Харрисона.
- Как настроить четвертную запятую, означающую один
- Индекс архива на Wayback Machine Музыкальные фрагменты, сыгранные в разных стилях - mp3 не архивируются
- Введение Кайла Ганна в исторические настройки есть объяснение того, как работает средний темперамент.
- Виллем Крезберген, Эндрю Круикшанк: Meantone, неравный и равный темперамент во времена J.S. Жизнь Баха https://www.academia.edu/9189419/Blankenburg_Equal_or_unequal_temperament_during_J.S._Bach_s_life



