WikiDer > Пифагорейская запятая

В музыкальный тюнинг, то Пифагорейская запятая (или же дитоническая запятая[а]), названный в честь древнего математика и философа Пифагор, это маленький интервал (или же запятая) существующие в Пифагорейский тюнинг между двумя энгармонически эквивалентный ноты, такие как C и B♯ (![]() Играть в (Помогите·Информация)), или D♭ и C♯.[1] Он равен соотношение частот (1.5)12⁄27 = 531441⁄524288 ≈ 1,01364, или около 23,46 центы, примерно четверть полутон (между 75:74 и 74:73[2]). Запятая, которая музыкальные темпераменты часто относятся к закалке, это пифагорейская запятая.[3]
Играть в (Помогите·Информация)), или D♭ и C♯.[1] Он равен соотношение частот (1.5)12⁄27 = 531441⁄524288 ≈ 1,01364, или около 23,46 центы, примерно четверть полутон (между 75:74 и 74:73[2]). Запятая, которая музыкальные темпераменты часто относятся к закалке, это пифагорейская запятая.[3]
Запятую Пифагора также можно определить как разницу между Пифагоров апотом и Пифагорейская лимма[4] (т.е. между хроматическим и диатоническим полутон, как определено в пифагорейской настройке), или разница между двенадцатью только идеальные квинты и семь октавы, или разница между тремя пифагорейскими дитоны и одну октаву (по этой причине пифагорейскую запятую также называют дитоническая запятая).
В уменьшился второйв пифагорейской настройке определяется как разница между лиммой и апотомом. Следовательно, он совпадает с противоположностью пифагорейской запятой и может рассматриваться как нисходящий Пифагорова запятая (например, из C♯ к D♭), что составляет примерно -23,46 цента.
Вывод
Как описано во введении, запятая Пифагора может быть получена несколькими способами:
- Разница между двумя энгармонически эквивалентный ноты в шкале Пифагора, например C и B♯ (
 Играть в (Помогите·Информация)), или D♭ и C♯ (увидеть ниже).
Играть в (Помогите·Информация)), или D♭ и C♯ (увидеть ниже). - Разница между Пифагоров апотом и Пифагорейская лимма.
- Разница между двенадцатью всего идеальные квинты и семь октавы.
- Разница между тремя пифагорейцами дитоны (основные трети) и одну октаву.
Просто идеальный пятый имеет соотношение частот из 3: 2. Он используется в настройке Пифагора вместе с октавой как критерий для определения соотношения частот любой другой ноты относительно данной начальной ноты.
Апотом и лимма - это два вида полутоны определен в пифагорейской настройке. А именно, апотом (около 113,69 цента, например, от C до C♯) - хроматический полутон, или усиленный унисон (A1), а лимма (около 90,23 цента, например, от C до D♭) - диатонический полутон, или минорная секунда (m2).
Дитон (или большая треть) представляет собой интервал, образованный двумя основные тона. В пифагорейской настройке размер основного тона составляет около 203,9 цента (соотношение частот 9: 8), таким образом, пифагорейский дитон составляет около 407,8 цента.
Размер
Размер пифагорейской запятой, измеренный в центы, является
или, точнее, с точки зрения частотные отношения:

Круг пятых и энгармоническое изменение
Пифагорейскую запятую также можно рассматривать как несоответствие между двенадцатью справедливо настроенный идеальные квинты (соотношение 3: 2) (![]() играть в (Помогите·Информация)) и семь октав (соотношение 2: 1):
играть в (Помогите·Информация)) и семь октав (соотношение 2: 1):
|
|
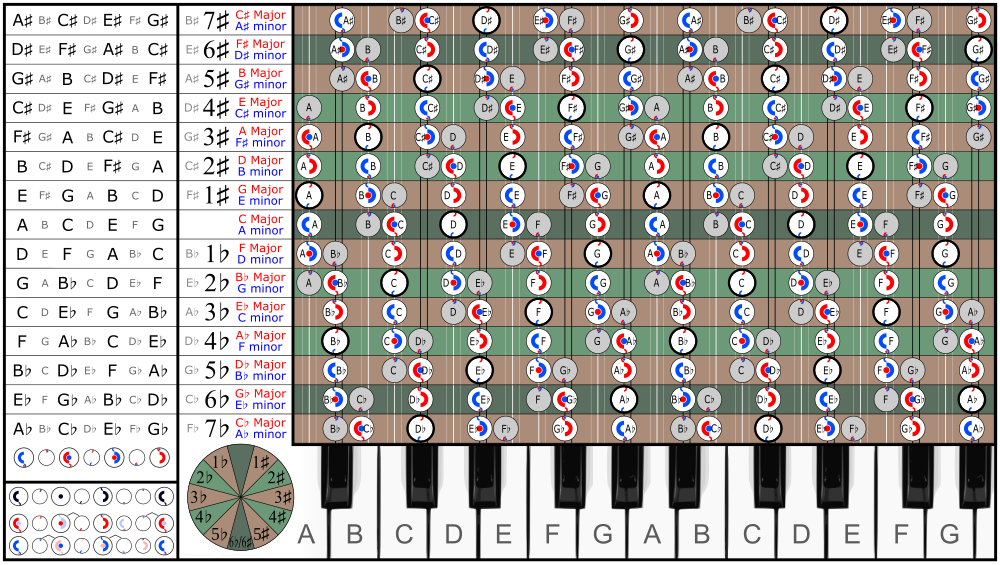
В следующей таблице музыкальные гаммы в круг пятых, запятая Пифагора видна как небольшой интервал между, например, F♯ и G♭.
6♭ и 6♯ шкалы * не идентичны - даже если они фортепианная клавиатура - но ♭ шкала на одну пифагорейскую запятую ниже. Игнорирование этой разницы приводит к энгармоническое изменение.
* 7♭ и 5♯соответственно 5♭ и 7♯ шкалы различаются одинаково одной пифагоровой запятой. Весы с семь случайностей используются редко, поскольку энгармонические шкалы с пятью случайностями рассматриваются как эквивалентные.
Этот интервал имеет серьезные последствия для различных настройка схемы хроматическая шкалапотому что в западной музыке 12 идеальных пятых и семь октав рассматриваются как один и тот же интервал. Равный темперамент, самая распространенная сегодня система настройки, используемая на Западе, согласовала это, сглаживая каждую пятую часть на двенадцатую пифагорейскую запятую (приблизительно 2 цента), создавая таким образом идеальные октавы.
Другой способ выразить это: только квинта имеет соотношение частот (по сравнению с тоникой) 3: 2 или 1,5 к 1, тогда как седьмой полутон (основанный на 12 равных логарифмических делениях октавы) является седьмой степенью корень двенадцатой степени из двух или 1.4983 ... к 1, что не совсем то же самое (примерно на 0,1%). Возьмите пятую часть в двенадцатую степень, затем вычтите семь октав, и вы получите пифагорейскую запятую (разница примерно 1,4%).
История
Первым, кто упомянул пропорцию запятой 531441: 524288, был Евклид, который берет за основу весь тон пифагорейской настройки с соотношением 9: 8, октаву с соотношением 2: 1 и число A = 262144. Он заключает, что увеличение этого числа на шесть полных тонов дает значение G, которая больше, чем полученная при ее повышении на октаву (в два раза больше A). Он дает G равным 531441.[5] Необходимые расчеты гласят:
Расчет G:
Вычисление двойника A:
Китайские математики знали о пифагорейской запятой еще в 122 г. до н.э. (ее расчет подробно описан в Хуайнаньцзы), и около 50 г. до н.э., Чинг Фанг обнаружил, что если бы цикл полных квинт продолжался от 12 до 53, разница между этой 53-й высотой и начальной высотой была бы намного меньше, чем запятая Пифагора. Этот гораздо меньший интервал позже был назван Запятая Меркатора (увидеть: история 53 равных темпераментов).
У Джорджа Рассела Лидийская хроматическая концепция тональной организации (1953) полушаг между лидийским тоником и ♭2 в его гаммах «Измененный мажор» и «Младший вспомогательный уменьшенный блюз» теоретически основан на интервале пифагорейской запятой.[6]
Смотрите также
Примечания
- ^ не путать с диатоническая запятая, более известный как синтоническая запятая, равное соотношению частот 81:80, или около 21,51 цента. См .: Джонстон Б. (2006). "Максимальная ясность" и другие сочинения о музыке, под редакцией Боба Гилмора. Урбана: Университет Иллинойса Press. ISBN 0-252-03098-2.
Рекомендации
- ^ Апель, Вилли (1969). Гарвардский музыкальный словарь, с.188. ISBN 978-0-674-37501-7. «... разница между двумя полутонами пифагорейской гаммы ...»
- ^ Гинзбург, Джекитиэль (2003). Scripta Mathematica, с.287. ISBN 978-0-7661-3835-3.
- ^ Койн, Ричард (2010). Настройка места: пространство для общения и повсеместные цифровые медиа, стр.45. ISBN 978-0-262-01391-8.
- ^ Коттик, Эдвард Л. (1992). Руководство для владельца клавесина, с.151. ISBN 0-8078-4388-1.
- ^ Евклид: Кататомэ Канонос (лат. Sectio canonis). Англ. перевод в: Эндрю Баркер (Ред.): Греческие музыкальные произведения. Vol. 2: Гармоническая и акустическая теория, Cambridge Mass: Cambridge University Press, 2004, стр. 190–208, здесь: стр. 199.
- ^ Рассел, Джордж (2001) [1953]. Джорджа Рассела Лидийская хроматическая концепция тональной организации. Том первый: Искусство и наука о тональной гравитации (Четвертое (второе издание, исправленное, 2008 г.) изд.). Бруклин, Массачусетс: издательская компания концепции. С. 17, 57-59. ISBN 0-9703739-0-2.