WikiDer > Функционально-ориентированное программирование
Эта статья слишком полагается на Рекомендации к основные источники. (Март 2018 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
В компьютерное программирование, функционально-ориентированное программирование (FOP) или же функционально-ориентированная разработка программного обеспечения (FOSD) это парадигма программирования для генерации программ в линейки программных продуктов (SPL) и для инкрементальной разработки программ.
История
FOSD возникла из многоуровневых конструкций и уровней абстракции в сетевых протоколах и расширяемых системах баз данных в конце 1980-х годов.[1] Программа представляла собой стопку слоев. Каждый слой добавлял функциональность к ранее составленным слоям, а различные композиции слоев создавали разные программы. Неудивительно, что для выражения таких замыслов требовался компактный язык. Элементарная алгебра соответствовала всем требованиям: каждый слой был функцией ( преобразование программы), который добавил новый код к существующей программе для создания новой программы, а дизайн программы моделировался выражением, то есть композицией преобразований (слоев). На рисунке слева показано наложение слоев i, j и h (где h находится внизу, а i - вверху). Алгебраические обозначения i (j (h)), i • j • h и i + j + h использовались для выражения этих планов.
Со временем слои были приравнены к объектам, где особенность является приращением функциональности программы. Было признано, что парадигма разработки и генерации программ является результатом оптимизации реляционных запросов, где программы оценки запросов были определены как выражения реляционной алгебры, а оптимизация запросов - это оптимизация выражений.[2] Линия программных продуктов - это семейство программ, в которых каждая программа определяется уникальным набором функций. С тех пор FOSD превратился в изучение модульности функций, инструментов, анализа и методов проектирования для поддержки создания программ на основе функций.
Второе поколение исследований FOSD было посвящено взаимодействию функций, которое зародилось в телекоммуникациях. функционально-ориентированное программирование был придуман;[3] эта работа раскрыла взаимодействие между слоями. Взаимодействия требуют адаптации функций при совмещении с другими функциями.
Третье поколение исследований было сосредоточено на том факте, что каждая программа имеет несколько представлений (например, исходный код, make-файлы, документация и т. Д.), И добавление функции в программу должно проработать каждое из ее представлений так, чтобы все они были согласованными. Кроме того, некоторые представления могут быть сгенерированы (или получены) из других. В нижеследующих разделах представлена математика трех последних поколений FOSD, а именно GenVoca,[1] ПРЕДСТОЯЩИЙ,[4] и FOMDD[5][6] описаны и приведены ссылки на линейки продуктов, которые были разработаны с использованием инструментов FOSD. Кроме того, приведены четыре дополнительных результата, применимых ко всем поколениям FOSD: Метамодели FOSD, Кубы программы FOSD, и взаимодействия функций FOSD.
GenVoca
GenVoca (а чемодан имен Genesis и Avoca)[1] - это композиционная парадигма для определения программ линейки продуктов. Базовые программы - это нулевые функции или преобразования, называемые значения:
f - базовая программа с функцией f h - базовая программа с функцией h
а функции - это унарные функции / преобразования, которые уточняют (модифицируют, расширяют, уточняют) программу:
i + x - добавляет функцию i в программу x j + x - добавляет функцию j в программу x
где + обозначает композицию функций. В дизайн программы - это именованное выражение, например:
п1 = j + f - программа p1 имеет особенности j и f p2 = j + h - программа p2 имеет особенности j и h p3 = i + j + h - программа p3 имеет особенности i, j и h
А Модель GenVoca домена или линейки программных продуктов представляет собой набор базовых программ и функций (см. МетаМодели и Программные кубикиПрограммы (выражения), которые могут быть созданы, определяют линейку продуктов. Оптимизация выражения оптимизация дизайна программы, а оценка выражения - генерация программы.
- Примечание: GenVoca основана на поэтапной разработке программ: процессе, который подчеркивает простоту дизайна и понятность, которые являются ключом к пониманию программ и автоматизированному построению программ. Рассмотрим программу p3 выше: он начинается с базовой программы h, затем добавляется функция j (читайте: функциональность функции j добавляется в кодовую базу h), и, наконец, добавляется функция i (читайте: функциональность функции i добавляется в базу кода из j • h).
- Примечание: не все комбинации функций имеют смысл. Функциональные модели (которые могут быть переведены в пропозициональные формулы) являются графическими представлениями, которые определяют допустимые комбинации функций.[7]
- Примечание: более поздняя формулировка GenVoca - симметричный: есть только одна базовая программа, 0 (пустая программа), и все функции являются унарными функциями. Это наводит на мысль о том, что GenVoca составляет программные структуры с помощью суперпозиция, идея о том, что сложные структуры состоят из наложения более простых структур.[8][9] Еще одна переформулировка GenVoca - это моноид: модель GenVoca - это набор функций с операцией композиции (•); композиция ассоциативна, и есть элемент идентичности (а именно 1, функция идентичности). Хотя возможны все композиции, не все они имеют смысл. Это причина для особенности моделей.
Функции GenVoca изначально были реализованы с использованием препроцессора C (#ifdef feature ... #endif) техники. Более продвинутый метод, называемый слои миксина, показали связь функций с объектно-ориентированными проектами, основанными на совместной работе.
ПРЕДСТОЯЩИЙ
Алгебраические иерархические уравнения для разработки приложений (ПРЕДСТОЯЩИЙ)[4] обобщил GenVoca двумя способами. Сначала он раскрыл внутреннюю структуру значений GenVoca в виде кортежей. Каждая программа имеет несколько представлений, таких как исходный код, документация, байт-код и make-файлы. Значение GenVoca - это кортеж программных представлений. В линейке продуктов парсеров, например, базовый парсер f определяется его грамматикой gж, Исходники Javaж, и документация dж. Парсер f моделируется кортежем f = [gж, сж, dж]. Каждое представление программы может иметь подпредставления, и они тоже могут иметь подпредставления рекурсивно. В общем, значение GenVoca - это кортеж вложенных кортежей, которые определяют иерархию представлений для конкретной программы.
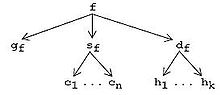
Пример. Предположим, терминальные представления - это файлы. В AHEAD грамматика gж соответствует одному файлу BNF, источник sж соответствует кортежу файлов Java [c1… Cп], и документация dж представляет собой кортеж файлов HTML [h1…часk]. Значение GenVoca (вложенные кортежи) можно изобразить в виде ориентированного графа: график для парсера f показан на рисунке справа. Стрелки обозначают проекции, то есть отображения кортежа в один из его компонентов. AHEAD реализует кортежи как файловые каталоги, поэтому f - это каталог, содержащий файл g.ж и подкаталоги sж и гж. Аналогично каталог sж содержит файлы c1… Cп, а каталог df содержит файлы h1…часk.
- Примечание. Файлы можно иерархически разложить дальше. Каждый класс Java может быть разложен на кортеж из членов и других объявлений классов (например, блоки инициализации и т. Д.). Важная идея здесь в том, что математика AHEAD рекурсивна.
Во-вторых, AHEAD представляет функции как вложенные кортежи унарных функций, называемых дельты. Дельты могут быть уточнения программы (преобразования с сохранением семантики), расширения (преобразования, расширяющие семантику), или взаимодействия (трансформации, изменяющие семантику). Мы используем нейтральный термин «дельта» для обозначения всех этих возможностей, поскольку каждая из них встречается в FOSD.
Для иллюстрации предположим, что функция j расширяет грамматику на граммj (добавлены новые правила и токены), расширяет исходный код на sj (добавляются новые классы и члены, а существующие методы изменяются) и расширяет документацию за счет dj. Набор дельт для признака j моделируется следующим образом: j = [граммj,sj,dj], которую мы называем дельта кортеж. Элементы дельта-кортежей сами могут быть дельта-кортежами. Пример: sj представляет изменения, которые вносятся в каждый класс в sж по признаку j, т. е. sj=[c1…cп]. Представления программы рекурсивно вычисляются путем сложения вложенных векторов. Представления для парсера p2 (чье выражение GenVoca равно j + f):
п2 = j + f - Выражение GenVoca = [граммj, sj, dj] + [гж, сж, dж] - подстановка = [граммj+ гж, sj+ sж, dj+ dж] - составлять кортежи поэлементно
То есть грамматика p2 базовая грамматика, составленная с ее расширением (граммj+ гж), источник p2 базовый источник, составленный с его расширением (sj+ sж), и так далее. Поскольку элементы дельта-кортежей сами могут быть дельта-кортежами, составные рекурсии, например, sj+ sж= [c1…cп] + [c1… Cп]=[c1+ c1…cп+ cп]. Подводя итог, значения GenVoca представляют собой вложенные кортежи программных артефактов, а функции - вложенные дельта-кортежи, где + рекурсивно составляет их путем сложения векторов. В этом суть AHEAD.
Представленные выше идеи конкретно раскрывают два принципа FOSD. В Принцип единообразия утверждает, что все программные артефакты обрабатываются и модифицируются одинаково. (Об этом свидетельствуют приведенные выше дельты для разных типов артефактов). В Принцип масштабируемости утверждает, что все уровни абстракций рассматриваются одинаково. (Это приводит к иерархическому вложению кортежей выше).
Первоначальной реализацией AHEAD является набор инструментов AHEAD и язык Jak, который демонстрирует как принципы единообразия, так и масштабируемости. Инструменты следующего поколения включают CIDE[10]и FeatureHouse.[11]
FOMDD
Функционально-ориентированный дизайн на основе модели (FOMDD)[5][6] сочетает в себе идеи AHEAD с Модельно-ориентированный дизайн (MDD) (он же Модельно-ориентированная архитектура (MDA)). Функции AHEAD фиксируют локальное обновление программных артефактов при добавлении функции в программу. Но есть и другие функциональные связи между программными артефактами, которые выражают производные. Например, связь между грамматикой gж и его источник синтаксического анализатора sж определяется инструментом компилятор-компилятор, например javacc. Точно так же отношения между исходными кодами Javaж и его байт-код bж определяется компилятором javac. А схема коммутации выражает эти отношения. Объекты - это программные представления, стрелки вниз - это производные, а горизонтальные стрелки - это дельты. На рисунке справа показана диаграмма коммутации для программы p.3 = я + j + h = [g3, с3, б3].
Основное свойство схема коммутации в том, что все пути между двумя объектами эквивалентны. Например, один из способов получить байт-код b3 парсера p3 (нижний правый объект на рисунке справа) из грамматики gчас парсера h (верхний левый объект) должен получить байт-код bчас и уточним до b3, а другой способ уточняет gчас к г3, а затем получить b3, где + представляет собой дельта-композицию, а () - функцию или инструментальное приложение:
б3 = бj + бя + javacc (javac (gчас )) = javac (javacc ( граммя + граммj + гчас ) )
Есть возможные пути получения байт-кода b3 парсера p3 из грамматики gчас парсера h. Каждый путь представляет собой метапрограмма чье выполнение порождает целевой объект (b3) от стартового объекта (gж). Возможная оптимизация: обход каждой стрелки схема коммутации имеет свою стоимость. Самый дешевый (т.е. самый короткий) путь между двумя объектами в схема коммутации это геодезический, который представляет собой наиболее эффективную метапрограмму, которая создает целевой объект из данного объекта.
- Примечание. «Показатель стоимости» не обязательно должен быть денежным значением; Стоимость может быть измерена временем производства, пиковыми или общими требованиями к памяти, потребляемой мощности или некоторым неформальным показателем, таким как «простота объяснения», или комбинацией вышеперечисленного (например, многокритериальная оптимизация). Идея геодезической является общей, и ее следует понимать и ценить в этом более общем контексте.
- Примечание. На геодезической может быть m начальных объектов и n конечных объектов; когда m = 1 и n> 1, это Направленная проблема дерева Штейнера, что NP-сложно.
Диаграммы поездок важны по крайней мере по двум причинам: (1) существует возможность оптимизации генерации артефактов (например, геодезических) и (2) они определяют различные способы построения целевого объекта из исходного объекта.[5][12] Путь через диаграмму соответствует цепочке инструментов: для того, чтобы модель FOMDD была согласованной, необходимо доказать (или продемонстрировать путем тестирования), что все цепочки инструментов, которые сопоставляют один объект с другим, на самом деле дают эквивалентные результаты. Если это не так, то либо есть ошибка в одном или нескольких инструментах, либо модель FOMDD неверна.
- Примечание: приведенные выше идеи были вдохновлены теория категорий.[5][6]
Приложения
- Сетевые протоколы
- Расширяемые системы баз данных
- Структуры данных
- Распределенный симулятор огневой поддержки армии
- Компилятор производственной системы
- Линия продуктов Graph
- Расширяемые препроцессоры Java
- Веб-портлеты
- Приложения SVG
Смотрите также
- Метамодели FOSD- продуктовые линейки продуктовых линеек
- FOSD оригами
- Кубики программы FOSD- многомерные продуктовые линейки
Рекомендации
- ^ а б c «Проектирование и реализация иерархических программных систем с повторно используемыми компонентами» (PDF).
- ^ «Выбор пути доступа в реляционных базах данных».
- ^ «Функционально-ориентированное программирование: новый взгляд на объекты». Архивировано из оригинал на 2003-08-03. Получено 2015-12-16.
- ^ а б «Масштабирование пошагового уточнения» (PDF).
- ^ а б c d «Разработка на основе модели, ориентированной на функции: пример портлетов» (PDF).
- ^ а б c Трухильо, Сальвадор; Азанза, Майдер; Диас, Оскар (октябрь 2007 г.). «Генеративное метапрограммирование». GPCE '07: Материалы 6-й международной конференции по генеративному программированию и компонентной инженерии: 105–114. Дои:10.1145/1289971.1289990.
- ^ «Модели характеристик, грамматики и формулы высказываний» (PDF).
- ^ «Алгебра функций и их композиции» (PDF).
- ^ «Наложение: независимый от языка подход к составлению программного обеспечения» (PDF).
- ^ «Гарантия синтаксической корректности для всех вариантов линейки продуктов: независимый от языка подход» (PDF).
- ^ «FeatureHouse: автоматическая композиция программного обеспечения, не зависящая от языка» (PDF).
- ^ «Тестирование программных продуктов с использованием генерации дополнительных тестов» (PDF).