WikiDer > Полевая линия
А полевая линия графический наглядное пособие для визуализации векторные поля. Он состоит из направленной линии, которая касательная в поле вектор в каждой точке по его длине.[1][2] Диаграмма, показывающая представительный набор соседних линий поля, является распространенным способом изображения векторного поля в научной и математической литературе; это называется диаграмма силовых линий. Они используются, чтобы показать электрические поля, магнитные поля, и гравитационные поля среди многих других типов. В механика жидкости линии поля, показывающие скорость поле поток жидкости называются рационализирует.
Определение и описание
А векторное поле определяет направление и величину в каждой точке пространства. Линия поля для этого векторного поля может быть построена, начав с точки и проведя линию через пространство, которая следует направлению векторного поля, сделав линию поля касательная к вектору поля в каждой точке.[3][2][1] Линия поля обычно отображается как направленный отрезок линии со стрелкой, указывающей направление векторного поля. Для двумерных полей силовые линии представляют собой плоские кривые, и большинство диаграмм силовых линий относятся к этому типу. Поскольку в каждой точке, где оно не равно нулю и конечно, векторное поле имеет уникальное направление, силовые линии никогда не могут пересекаться, поэтому через каждую точку проходит ровно одна силовая линия, в которой векторное поле ненулевое и конечное.[3][2] Точки, где поле равно нулю или бесконечности, не проходят через линии поля, поскольку направление не может быть определено там, но может быть конечные точки линий поля.
Поскольку существует бесконечное количество точек, можно провести бесконечное количество линий поля; но только ограниченное количество может быть показано на диаграмме линий поля. Следовательно, какие линии поля показаны, это выбор, сделанный человеком или компьютерной программой, которая рисует диаграмму, и одно векторное поле может быть изображено разными наборами линий поля. Диаграмма линий поля обязательно является неполным описанием векторного поля, поскольку она не дает информации о поле между нарисованными линиями поля, а выбор того, сколько и какие линии показывать, определяет, сколько полезной информации дает диаграмма.
Линии поля будут начинаться у источника векторного поля, где его дивергенция положительна. Полевые линии, уходящие в сток векторного поля, где расходимость отрицательная, будут иметь свой конец. Полевые линии также могут образовывать замкнутые петли, или простираются до бесконечности, или продолжаются вечно, не замыкаясь на самих себе.[4] Отдельная линия поля показывает направление векторного поля, но не величина. Чтобы также изобразить величина поля можно нарисовать набор линий поля так, чтобы плотность линий поля (количество линий поля на единицу перпендикулярной площади) в любом месте была пропорциональна величине векторного поля в этой точке. Области, в которых соседние силовые линии сходятся (становятся ближе друг к другу), указывают на то, что поле усиливается в этом направлении.
В физике рисунки силовых линий в основном полезны в тех случаях, когда источники и поглотители, если таковые имеются, имеют физическое значение, в отличие, например, от случай силового поля радиальная гармоника. Например, Закон Гаусса заявляет, что электрическое поле имеет источники в положительных обвинения, опускается на отрицательные заряды, и ни в каком другом месте, поэтому силовые линии электрического поля начинаются с положительных зарядов и заканчиваются отрицательными зарядами. Гравитационное поле не имеет источников, оно опускается на массы и не имеет нигде больше, силовые линии гравитационного поля исходят из бесконечности и заканчиваются на массах. А магнитное поле не имеет источников и стоков (Закон Гаусса для магнетизма), поэтому его линии поля не имеют начала и конца: они могут Только образуют замкнутые петли, простираются до бесконечности в обоих направлениях или продолжаются бесконечно, никогда не пересекая себя.
Обратите внимание, что для этого вида чертежа, где плотность линий поля должна быть пропорциональна величине поля, важно представить все три измерения. Например, рассмотрим электрическое поле, возникающее от одного изолированного точечный заряд. Силовые линии электрического поля в этом случае представляют собой прямые линии, исходящие от заряда равномерно во всех направлениях в трехмерном пространстве. Это означает, что их плотность пропорциональна , правильный результат соответствует Закон Кулона для этого случая. Однако, если бы силовые линии электрического поля для этой установки были бы просто нарисованы на двумерной плоскости, их двумерная плотность была бы пропорциональна , неправильный результат для данной ситуации.[5]
Строительство
Учитывая векторное поле и отправная точка линия поля может быть построена итеративно путем нахождения вектора поля в этой точке . Единица касательный вектор в этот момент: . Двигаясь на небольшое расстояние по направлению поля можно найти новую точку на линии
Тогда поле в этой точке найден и движется дальше в этом направлении следующая точка линии поля. В каждой точке следующий пункт можно найти
Повторяя это и соединив точки, полевая линия может быть увеличена на сколько угодно. Это только приближение к фактической силовой линии, поскольку каждый прямой сегмент на самом деле не касается поля по его длине, а только в его начальной точке. Но используя достаточно маленькое значение для , делая большее количество более коротких шагов, силовая линия может быть аппроксимирована как угодно точно. Силовую линию можно продолжить в направлении, противоположном делая каждый шаг в противоположном направлении, используя отрицательный шаг .
Примеры
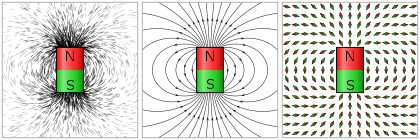
Если векторное поле описывает скорость поле, затем следуют линии поля линии потока в потоке. Возможно, наиболее знакомым примером векторного поля, описываемого линиями поля, является магнитное поле, который часто изображается с помощью силовых линий, исходящих от магнит.
Расхождение и локон
Линии поля можно использовать для отслеживания знакомых величин из векторное исчисление:
- Расхождение можно легко увидеть через силовые линии, если предположить, что линии нарисованы так, что плотность силовых линий пропорциональна величине поля (см. выше). В этом случае расхождение можно рассматривать как начало и конец силовых линий. Если векторное поле является результатом радиальных полей закона обратных квадратов по отношению к одному или нескольким источникам, то это соответствует тому факту, что расходимость такого поля равна нулю вне источников. В соленоидальное векторное поле (т.е. векторное поле, в котором дивергенция всюду равна нулю), силовые линии не начинаются и не заканчиваются; они либо образуют замкнутые петли, либо уходят в бесконечность в обоих направлениях. Если векторное поле имеет положительную дивергенцию в некоторой области, линии поля будут начинаться из точек в этой области. Если векторное поле имеет отрицательную дивергенцию в некоторой области, линии поля будут оканчиваться в точках в этой области.
- В Теорема Кельвина – Стокса показывает, что силовые линии векторного поля с нулевым завиток (т.е. консервативное векторное поле, например а гравитационное поле или электростатическое поле) не могут быть замкнутыми циклами. Другими словами, завиток всегда присутствует, когда линия поля образует замкнутый цикл. Он может присутствовать и в других ситуациях, например, спиральный форма силовых линий.
Физическое значение
Хотя силовые линии представляют собой «простую» математическую конструкцию, в некоторых случаях они приобретают физическое значение. В механика жидкости, силовые линии поля скорости (рационализирует) в установившемся потоке представляют собой пути движения частиц жидкости. В контексте физика плазмы, электроны или же ионы находящиеся на одной силовой линии сильно взаимодействуют, в то время как частицы на разных силовых линиях, как правило, не взаимодействуют. Такое же поведение проявляют частицы железной опилки в магнитном поле.
Железные опилки на фотографии кажутся выстраивающимися по дискретным силовым линиям, но ситуация более сложная. Это легко представить как двухэтапный процесс: во-первых, опилки равномерно распределяются по магнитному полю, но все выровнены в направлении поля. Затем, исходя из масштаба и ферромагнитный Свойства опилок они заглушают поле по обе стороны, создавая видимые промежутки между линиями, которые мы видим.[нужна цитата] Конечно, описанные здесь две стадии происходят одновременно, пока не будет достигнуто равновесие. Поскольку собственный магнетизм опилок изменяет поле, линии, показанные опилками, являются только приближением силовых линий исходного магнитного поля. Магнитные поля непрерывны и не имеют дискретных линий.
Смотрите также
- Силовое поле (физика)
- Полевые линии множеств Юлии
- Внешний луч - силовые линии потенциала Дуади – Хаббарда Набор Мандельброта или же заполненные наборы Джулии
- Силовая линия
- Векторное поле
Рекомендации
- ^ а б То, Стивен (2011). Визуализация полей и приложений в инженерии. Джон Уайли и сыновья. п. 64. ISBN 9780470978467.
- ^ а б c Даррант, Алан (1996). Векторы в физике и технике. CRC Press. С. 129–130. ISBN 9780412627101.
- ^ а б Haus, Herman A .; Мехиор, Джеймс Р. (1998). «Раздел 2.7: Визуализация полей, расхождения и завивки». Электромагнитные поля и энергия. Учебный центр гипермедиа, Массачусетский технологический институт. Получено 9 ноября 2019.
- ^ Либерхер, Мартин (6 июля 2010 г.). «Силовые линии магнитного поля спиральной катушки - не простые петли». Американский журнал физики. 78 (11): 1117–1119. Bibcode:2010AmJPh..78.1117L. Дои:10.1119/1.3471233.
- ^ А. Вольф, С. Дж. Ван Хук, Э. Р. Уикс, Диаграммы силовых линий электрического поля не работают Являюсь. J. Phys., Vol. 64, No. 6. (1996), pp. 714–724 DOI 10.1119 / 1.18237
дальнейшее чтение
- Гриффитс, Дэвид Дж. (1998). Введение в электродинамику (3-е изд.). Прентис Холл. стр.65–67 и 232. ISBN 978-0-13-805326-0.
внешняя ссылка
| Викискладе есть медиафайлы по теме Диаграммы полей. |
- Интерактивный Java-апплет, показывающий силовые линии электрического поля выбранных пар зарядов Вольфганг Бауэр
- «Визуализация полей, расхождения и завитка» заметки из курса Массачусетского технологического института.