WikiDer > Гауссовская адаптация
Эта статья поднимает множество проблем. Пожалуйста помоги Улучши это или обсудите эти вопросы на страница обсуждения. (Узнайте, как и когда удалить эти сообщения-шаблоны) (Узнайте, как и когда удалить этот шаблон сообщения)
|
Гауссова адаптация (GA), также называемый нормальный или же естественная адаптация (NA) является эволюционный алгоритм предназначен для максимизации выхода продукции из-за статистического отклонения значений компонентов обработка сигналов системы. Короче говоря, ГА - это стохастический адаптивный процесс, в котором несколько выборок п-мерный вектор Икс[ИксТ = (Икс1, Икс2, ..., Иксп)] взяты из многомерное распределение Гаусса, N(м, M), имея в виду м и матрица моментов M. Образцы проходят испытания на соответствие требованиям или отказам. Моменты первого и второго порядка гауссиана, ограниченного проходными выборками, равны м * иМ *.
Итог Икс как проходной образец определяется функцией s(Икс), 0 < s(Икс) < q ≤ 1, такое что s(Икс) - вероятность того, что x будет выбран в качестве проходной выборки. Средняя вероятность нахождения проходных выборок (выход) составляет
Тогда теорема GA утверждает:
Для любого s(Икс) и для любого значения п< q, всегда существует гауссовский p. d. f. [ функция плотности вероятности ], адаптированный для максимального рассеивания. Необходимые условия для локального оптимума: м = м* и M пропорционально M*. Решается и двойная проблема: п максимизируется при сохранении постоянной дисперсии (Kjellström, 1991).
Доказательства теоремы можно найти в статьях Kjellström, 1970, и Kjellström & Taxén, 1981.
Поскольку дисперсия определяется как экспонента энтропии / беспорядка /средняя информация сразу следует, что теорема верна и для этих понятий. В целом это означает, что гауссовская адаптация может одновременно максимизировать доходность и средняя информация (без какой-либо необходимости в доходности или средняя информация будут определены как целевые функции).
Теорема верна для всех областей приемлемости и всех гауссовых распределений.. Его можно использовать путем циклического повторения случайных вариаций и отбора (как естественная эволюция). В каждом цикле отбирается достаточно большое количество точек, распределенных по Гауссу, и проверяется их принадлежность к области приемлемости. Центр тяжести гауссиана, м, затем перемещается в центр тяжести утвержденных (выбранных) точек, м*. Таким образом, процесс сходится к состоянию равновесия, удовлетворяющему теореме. Решение всегда приблизительное, поскольку центр тяжести всегда определяется для ограниченного числа точек.
Впервые он был использован в 1969 году в качестве чистого алгоритма оптимизации, делающего области приемлемости все меньше и меньше (по аналогии с имитация отжига, Киркпатрик 1983). С 1970 года он используется как для обычной оптимизации, так и для максимизации доходности.
Естественная эволюция и гауссовская адаптация
Его также сравнивали с естественной эволюцией популяций живых организмов. В этом случае s(Икс) - вероятность того, что человек, имеющий массив Икс фенотипов выживут, дав потомство следующему поколению; определение индивидуальной пригодности, данное Хартлом 1981. Урожайность, п, заменяется на средний фитнес определяется как среднее значение по набору особей в большой популяции.
Фенотипы часто распределены по Гауссу в большой популяции, и необходимое условие для того, чтобы естественная эволюция могла выполнить теорему гауссовской адаптации по отношению ко всем гауссовским количественным признакам, состоит в том, что она может подтолкнуть центр тяжести гауссиана к центр тяжести выбранных особей. Это может быть выполнено Закон Харди – Вайнберга. Это возможно, потому что теорема о гауссовой адаптации справедлива для любой области приемлемости, независимо от структуры (Kjellström, 1996).
В этом случае правила генетической изменчивости, такие как кроссовер, инверсия, транспозиция и т.д., можно рассматривать как генераторы случайных чисел для фенотипов. Таким образом, в этом смысле гауссову адаптацию можно рассматривать как генетический алгоритм.
Как подняться на гору
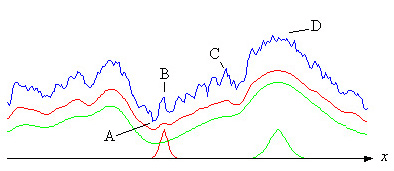
Среднее приспособление может быть вычислено при условии, что известно распределение параметров и структура ландшафта. Реальный ландшафт неизвестен, но на рисунке ниже показан вымышленный профиль (синий) ландшафта вдоль линии (x) в комнате, охватываемой такими параметрами. Красная кривая - это среднее значение на основе красной колоколообразной кривой в нижней части рисунка. Это достигается за счет скольжения колоколообразной кривой вдоль Икс-ось, вычисляя среднее значение в каждом месте. Как видно, сглаживаются небольшие пики и ямки. Таким образом, если эволюция начинается в точке A с относительно небольшой дисперсией (красная колоколообразная кривая), то подъем будет происходить на красной кривой. Процесс может застрять на миллионы лет в точках B или C, пока остаются пустоты справа от этих точек, а скорость мутаций слишком мала.
Если частота мутаций достаточно высока, беспорядок или дисперсия могут увеличиваться, и параметр (параметры) могут стать распределенными, как зеленая кривая колокола. Далее подъем будет происходить по зеленой кривой, которая еще более сглаживается. Поскольку впадины справа от B и C теперь исчезли, процесс может продолжаться до пиков в D. Но, конечно же, ландшафт накладывает ограничения на беспорядок или изменчивость. Кроме того - в зависимости от ландшафта - процесс может стать очень прерывистым, и если соотношение между временем, проведенным процессом на локальном пике, и временем перехода к следующему пику очень велико, он может также выглядеть как прерывистое равновесие как было предложено Гулдом (см. Ридли).
Компьютерное моделирование гауссовой адаптации
Пока что теория рассматривает только средние значения непрерывных распределений, соответствующих бесконечному числу людей. На самом деле, однако, количество особей всегда ограничено, что приводит к неопределенности в оценке м и M (матрица моментов гауссиана). И это тоже может сказаться на эффективности процесса. К сожалению, об этом известно очень мало, по крайней мере, теоретически.
Реализация нормальной адаптации на компьютере - довольно простая задача. Адаптация m может выполняться по одной выборке (индивидууму) за раз, например
- м(я + 1) = (1 – а) м(я) + топор
куда Икс это проходной образец, и а <1 подходящая константа, так что величина, обратная величине a, представляет количество особей в популяции.
M в принципе может обновляться после каждого шага у ведущий к возможной точке
- Икс = м + у в соответствии с:
- M(я + 1) = (1 – 2б) M(я) + 2покаТ,
куда уТ это транспонирование у и б << 1 - еще одна подходящая константа. Чтобы гарантировать подходящее увеличение средняя информация, у должно быть нормально распределенный с матрицей моментов μ2M, где скаляр μ > 1 используется для увеличения средняя информация (информационная энтропия, беспорядок, разнообразие) с подходящей скоростью. Но M никогда не будет использоваться в расчетах. Вместо этого мы используем матрицу W определяется WWТ = M.
Таким образом, мы имеем у = Wg, куда грамм нормально распределена с матрицей моментов μU, и U - единичная матрица. W и WТ может быть обновлен по формулам
- W = (1 – б)W + мимоТ и WТ = (1 – б)WТ + bgyТ
потому что умножение дает
- M = (1 – 2б)M + 2покаТ,
где термины, включающие б2 были заброшены. Таким образом, M будет косвенно адаптирован с хорошим приближением. На практике достаточно обновить W Только
- W(я + 1) = (1 – б)W(я) + мимоТ.
Это формула, используемая в простой двухмерной модели мозга, удовлетворяющей правилу ассоциативного обучения Хебба; см. следующий раздел (Kjellström, 1996 и 1999).
На рисунке ниже показан эффект увеличения средняя информация в гауссовском п.о.ф. используется для восхождения на гору Крест (две линии обозначают контурную линию). И красный, и зеленый кластеры имеют одинаковую среднюю пригодность, около 65%, но зеленый кластер имеет гораздо более высокое средняя информация делая зеленый процесс намного более эффективным. Эффект от этой адаптации не очень заметен в двумерном случае, но в многомерном случае эффективность процесса поиска может быть увеличена на много порядков.
Эволюция в мозгу
Предполагается, что в мозгу эволюция ДНК-сообщений должна быть заменена эволюцией сигнальных паттернов, а фенотипический ландшафт заменен ментальным ландшафтом, сложность которого вряд ли будет второстепенной. Метафора с ментальным ландшафтом основана на предположении, что определенные паттерны сигналов способствуют улучшению самочувствия или производительности. Например, управление группой мышц приводит к лучшему произношению слова или исполнению музыкального произведения.
В этой простой модели предполагается, что мозг состоит из взаимосвязанных компонентов, которые могут складывать, умножать и задерживать значения сигналов.
- Ядро нервной клетки может добавлять значения сигнала,
- синапс может размножаться с постоянной и
- Аксон может задерживать значения.
Это основа теории цифровых фильтров и нейронных сетей, состоящих из компонентов, которые могут складывать, умножать и задерживать значения сигналов, а также многих моделей мозга, Levine 1991.
На рисунке ниже предполагается, что ствол мозга доставляет гауссовские паттерны сигналов. Это возможно, поскольку определенные нейроны срабатывают случайным образом (Кандел и др.). Ствол также представляет собой неупорядоченную структуру, окруженную более упорядоченными оболочками (Bergström, 1969), и согласно Центральная предельная теорема сумма сигналов от многих нейронов может быть распределена по Гауссу. Треугольные прямоугольники представляют синапсы, а прямоугольники со знаком + - ядра клеток.
Предполагается, что сигналы коры головного мозга будут проверены на осуществимость. Когда сигнал принят, контактные области в синапсах обновляются в соответствии с приведенными ниже формулами в соответствии с теорией Хебба. На рисунке показано 2-мерное компьютерное моделирование гауссовской адаптации в соответствии с последней формулой в предыдущем разделе.
м и W обновляются в соответствии с:
- м1 = 0.9 м1 + 0.1 Икс1; м2 = 0.9 м2 + 0.1 Икс2;
- ш11 = 0.9 ш11 + 0.1 у1грамм1; ш12 = 0.9 ш12 + 0.1 у1грамм2;
- ш21 = 0.9 ш21 + 0.1 у2грамм1; ш22 = 0.9 ш22 + 0.1 у2грамм2;
Как видно, это очень похоже на маленький мозг, управляемый теорией Hebbian обучение (Kjellström, 1996, 1999 и 2002).
Гауссовская адаптация и свобода воли
Гауссова адаптация как эволюционная модель мозга, подчиняющаяся Хеббийская теория ассоциативного обучения предлагает альтернативный взгляд на свободная воля из-за способности процесса максимизировать среднее соответствие паттернов сигналов в мозгу, взбираясь на ментальный ландшафт по аналогии с фенотипической эволюцией.
Такой случайный процесс дает нам большую свободу выбора, но не дает. Однако иллюзия воли может проистекать из способности процесса максимизировать среднюю приспособленность, заставляя процесс стремиться к цели. То есть он предпочитает более высокие пики ландшафта более низким или лучшие альтернативы перед худшими. Так может появиться призрачная воля. Аналогичное мнение высказал Зохар 1990. См. Также Kjellström 1999.
Теорема эффективности случайного поиска
Эффективность гауссовой адаптации основана на теории информации Клода Э. Шеннона (см. информационное содержание). Когда событие происходит с вероятностью п, то информация −log (п) может быть достигнуто. Например, если средняя пригодность п, информация, полученная для каждого человека, выбранного для выживания, будет равна −log (п) - в среднем - и работа / время, необходимое для получения информации, пропорционально 1 /п. Таким образом, если эффективность, E, определяется как информация, деленная на работу / время, необходимое для ее получения, мы имеем:
- E = −п бревно(п).
Эта функция достигает максимума, когда п = 1/е = 0,37. Тот же результат был получен Гейнсом другим методом.
E = 0, если п = 0, для процесса с бесконечной скоростью мутации, и если п = 1, для процесса со скоростью мутации = 0 (при условии, что процесс жив). Этот показатель эффективности действителен для большого класса случайный поиск процессы при наличии определенных условий.
1 Поиск должен быть статистически независимым и одинаково эффективным по различным направлениям параметров. Это условие может быть выполнено приблизительно, если матрица моментов гауссиана была адаптирована для максимального средняя информация до некоторой области приемлемости, потому что линейные преобразования всего процесса не влияют на эффективность.
2 Все люди имеют равную стоимость, а производная п = 1 <0.
Тогда может быть доказана следующая теорема:
Все меры эффективности, которые удовлетворяют указанным выше условиям, асимптотически пропорциональны -п бревно(P / q), когда количество измерений увеличивается, и максимизируются на п = q exp (-1) (Kjellström, 1996 и 1999).
На рисунке выше показана возможная функция эффективности для процесса случайного поиска, такого как гауссовская адаптация. Слева процесс наиболее хаотичный, когда п = 0, а справа полный порядок, где п = 1.
В примере Rechenberg, 1971, 1973, случайное блуждание проталкивается через коридор, максимизируя параметр Икс1. В этом случае область приемлемости определяется как (п - 1) -мерный интервал в параметрах Икс2, Икс3, ..., Иксп, но Икс1-значение ниже последнего принятого никогда не будет принято. С п никогда не может превышать 0,5 в этом случае, максимальная скорость в сторону большего Икс1-значения достигнуты для п = 0.5/е = 0,18, что согласуется с выводами Рехенберга.
Точка зрения, которая также может представлять интерес в этом контексте, заключается в том, что для доказательства теоремы не требуется никакого определения информации (кроме того, что точки выборки внутри некоторой области приемлемости не дают информации о ее расширении). Затем, поскольку формулу можно интерпретировать как информацию, разделенную на работу, необходимую для получения информации, это также указывает на то, что −log (п) является хорошим кандидатом для измерения информации.
Алгоритм Штауффера и Гримсона
Гауссова адаптация также использовалась для других целей, например, для удаления тени с помощью «алгоритма Штауффера-Гримсона», который эквивалентен гауссовой адаптации, использованной в разделе «Компьютерное моделирование гауссовой адаптации» выше. В обоих случаях метод максимального правдоподобия используется для оценки средних значений путем адаптации по одной выборке за раз.
Но есть отличия. В случае Штауффера-Гримсона информация не используется для управления генератором случайных чисел для центрирования, максимизации средней пригодности, средняя информация или производственный доход. Адаптация матрицы моментов также сильно отличается по сравнению с «эволюцией в мозгу» выше.
Смотрите также
- Энтропия в термодинамике и теории информации
- Фундаментальная теорема естественного отбора Фишера
- Свободная воля
- Генетический алгоритм
- Hebbian обучение
- Информационное содержание
- Имитация отжига
- Стохастическая оптимизация
- Стратегия эволюции адаптации ковариационной матрицы (CMA-ES)
- Единица выбора
Рекомендации
- Бергстрём, Р. М. Энтропийная модель развивающегося мозга. Психобиология развития, 2(3): 139–152, 1969.
- Брукс, Д. Р., Уайли, Э. О. Эволюция как энтропия, к единой теории биологии. Издательство Чикагского университета, 1986.
- Брукс, Д. Р. Эволюция в информационную эпоху: новое открытие природы организма. Семиозис, Эволюция, Энергия, Развитие, Том 1, номер 1, март 2001 г.
- Гейнс, Брайан Р. Управление знаниями в обществах интеллектуальных адаптивных агентов. Журнал интеллектуальных информационных систем 9, 277–298 (1997).
- Хартл, Д. Л. Учебник по популяционной генетике. Синауэр, Сандерленд, Массачусетс, 1981.
- Гамильтон, WD. 1963. Эволюция альтруистического поведения. Американский натуралист 97: 354–356
- Кандел, Э. Р., Шварц, Дж. Х., Джессел, Т. М. Основы неврологии и поведения. Prentice Hall International, Лондон, 1995.
- С. Киркпатрик, К. Д. Гелатт, М. П. Векки, Оптимизация с помощью имитации отжига, Science, том 220, номер 4598, страницы 671–680, 1983.
- Кьельстрём, Г. Оптимизация сети путем случайного изменения значений компонентов. Ericsson Technics, т. 25, нет. 3. С. 133–151, 1969.
- Кьельстрём, Г. Оптимизация электрических сетей с учетом допустимых затрат. Ericsson Technics, нет. 3. С. 157–175, 1970.
- Кьельстрём Г. и Таксен Л. Стохастическая оптимизация в проектировании систем. IEEE Trans. на Circ. and Syst., vol. КАС-28, вып. 7 июля 1981 г.
- Кьельстрём Г., Таксен Л. и Линдберг П. О. Дискретная оптимизация цифровых фильтров с использованием гауссовой адаптации и минимизации квадратичной функции. IEEE Trans. на Circ. and Syst., vol. CAS-34, № 10, октябрь 1987 г.
- Кьельстрём, Г. Об эффективности гауссовой адаптации. Журнал теории оптимизации и приложений, т. 71, нет. 3 декабря 1991 г.
- Кьельстрём, Г. и Таксен, Л. Гауссовская адаптация, эффективный глобальный оптимизатор, основанный на эволюции; Вычислительная и прикладная математика, Ин, К. Брезински и У. Кулиш (редакторы), Elsevier Science Publishers B.V., стр. 267–276, 1992.
- Кьельстрём, Г. Эволюция как алгоритм статистической оптимизации. Эволюционная теория 11: 105–117 (январь 1996 г.).
- Кьелльстрём, Г. Эволюция мозга. Прикладная математика и вычисления, 98 (2–3): 293–300, февраль 1999 г.
- Кьельстрём, Г. Эволюция в двух словах и некоторые следствия, касающиеся оценок. ЭВОЛЮЦИОНИРОВАТЬ, ISBN 91-972936-1-X, Стокгольм, 2002.
- Левин, Д. С. Введение в нейронное и когнитивное моделирование. Лоуренс Эрлбаум Ассошиэйтс, Инк., Издательство, 1991.
- Маклин, П. Д. Триединая концепция мозга и поведения. Торонто, Univ. Торонто Пресс, 1973.
- Мейнард Смит, Дж. 1964. Групповой отбор и родственный отбор, Nature 201: 1145–1147.
- Мэйнард Смит, Дж. Эволюционная генетика. Издательство Оксфордского университета, 1998.
- Майр, Э. Что такое эволюция. Основные книги, Нью-Йорк, 2001.
- Мюллер, Кристиан Л. и Сбальзарини Иво Ф. Возвращение к гауссовской адаптации - энтропийный взгляд на адаптацию ковариационной матрицы. Институт теоретической информатики и Швейцарский институт биоинформатики, ETH Цюрих, CH-8092 Цюрих, Швейцария.
- Пинель, Дж. Ф. и Сингхал, К. Статистическое проектирование, центрирование и допуски с использованием параметрической выборки. IEEE Transactions on Circuits and Systems, Vol. Дас-28, № 7, июль 1981 г.
- Рехенберг И. (1971): Evolutionsstrategie - Optimierung technischer Systeme nach Prinzipien der biologischen Evolution (докторская диссертация). Перепечатано Фромман-Хольцбугом (1973).
- Ридли, М. Эволюция. Blackwell Science, 1996.
- Stauffer, C. & Grimson, W.E.L. Модели обучения с использованием отслеживания в реальном времени, IEEE Trans. на ПАМИ, 22 (8), 2000.
- Стир Г. Об исследовании возможностей аналоговых интегральных схем в космосе. Technischen Universität Munchen, Диссертация 2005.
- Таксен, Л. Рамки координации развития сложных систем. Технологический институт Университета Линчёпинга, диссертация, 2003.
- Зохар, Д. Квантовое Я: революционный взгляд на человеческую природу и сознание, основанный на новой физике. Лондон, Блумсбери, 1990.