WikiDer > Геодезический многогранник

Geodesic polyhedron

3 конструкции на {3,5+}_6,0



Икосаэдр и связанные многогранники симметрии могут использоваться для определения высокого геодезического многогранника путем разделения треугольных граней на меньшие треугольники и проецирования всех новых вершин на сферу. Многоугольные грани более высокого порядка можно разделить на треугольники, добавив новые вершины с центром на каждой грани. Новые лица на сфере не равносторонние треугольники, но они примерно равны по длине ребра. Все вершины имеют валентность-6, за исключением 12 вершин, которые имеют валентность 5.

Строительство {3,5+}_3,3

Геодезическое подразделение также может быть выполнено с помощью увеличенного додекаэдра, разделив пятиугольники на треугольники с центральной точкой и разделив их.

Строительство {3,5+}_6,3

Киральные многогранники с многоугольными гранями более высокого порядка могут быть дополнены центральными точками и новыми треугольными гранями. Затем эти треугольники можно разделить на более мелкие треугольники для новых геодезических многогранников. Все вершины имеют валентность-6, кроме 12 с центром в исходных вершинах, которые имеют валентность 5.

Построение смешанной геодезической формы

Геодезическое подразделение также может быть выполнено с помощью увеличенных квадратных граней, хотя в результате треугольники будут рядом с прямоугольными, а не равносторонними. Этот ромбикосододекаэдр Пример имеет от 4 до 7 треугольников вокруг каждой вершины.

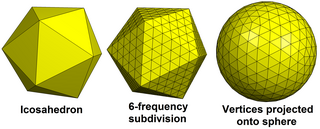
А геодезический многогранник выпуклый многогранник из треугольников. У них обычно есть икосаэдрическая симметрия, такое, что у них есть 6 треугольников в вершине, кроме 12 вершин, у которых есть 5 треугольников. Они двойной соответствующих Многогранники Гольдберга в основном с шестиугольными гранями.

Геодезические многогранники являются хорошим приближением к сфере для многих целей и появляются во многих различных контекстах. Самым известным может быть геодезические купола разработано Бакминстер Фуллер, именем которых названы геодезические многогранники. Геодезические сетки используется в геодезия также имеют геометрию геодезических многогранников. В капсиды некоторых вирусы имеют форму геодезических многогранников,^[1]^[2] и фуллерен молекулы имеют форму Многогранники Гольдберга. Геодезические многогранники доступны как геометрические примитивы в Программный пакет Blender для 3D-моделирования, который называет их икосферы: они являются альтернативой УФ-сфера, имеющий более регулярное распределение вершин, чем УФ-сфера.^[3]^[4] В Построение Гольдберга – Кокстера. является расширением понятий, лежащих в основе геодезических многогранников.

Геодезические обозначения

В Магнус Веннингерс Сферические модели, многогранники заданы геодезические обозначения в виде {3,q+}_б,c, куда {3,q} это Символ Шлефли для правильного многогранника с треугольными гранями, а q-валентность вершины. В + символ указывает на валентность увеличиваемых вершин. б,c представляют собой описание подразделения, где 1,0 представляет базовую форму. Существует 3 класса симметрии форм: {3,3+}_1,0 для тетраэдр, {3,4+}_1,0 для октаэдр, и {3,5+}_1,0 для икосаэдр.

Двойное обозначение для Многогранники Гольдберга является {q+,3}_б,c, с вершинами валентности-3, с q-угольные и шестиугольные грани. Существует 3 класса симметрии форм: {3 +, 3}_1,0 для тетраэдр, {4+,3}_1,0 для куб, и {5 +, 3}_1,0 для додекаэдр.

Ценности для б,c делятся на три класса:

I класс (b = 0 или c = 0): {3,q+}_б,0 или же {3,q+}_0,б представляют собой простое разделение с исходными ребрами, разделенными на б суб-края.

II класс (b = c): {3,q+}_б,б легче увидеть из двойственный многогранник {q, 3} с q-угольные грани сначала разбиваются на треугольники с центральной точкой, а затем все ребра разбиваются на б суб-края.

III класс: {3,q+}_б,c имеют ненулевые неравные значения для б,c, и существуют в киральных парах. За б > c мы можем определить его как правую форму, и c > б левосторонняя форма.

Подразделения класса III здесь не просто совпадают с исходными краями. Подсетки можно извлечь, посмотрев на треугольная черепица, расположив большой треугольник поверх вершин сетки и пешеходных дорожек из одной вершины б шаги в одном направлении и поворот по часовой или против часовой стрелки, а затем другой c шаги к следующей первичной вершине.

Например, икосаэдр составляет {3,5+}_1,0, и пентакид додекаэдр, {3,5+}_1,1 рассматривается как правильный додекаэдр с пятиугольными гранями, разделенными на 5 треугольников.

Первичная грань подразделения называется главный многогранный треугольник (PPT) или структура разбивки. Вычисление одного PPT позволяет создать всю фигуру.

В частота геодезического многогранника определяется суммой ν = б + c. А гармонический является подчастотой и может быть любым целым делителем ν. Второй класс всегда имеет гармонику 2, так как ν = 2б.

В число триангуляции является Т = б² + до н.э + c². Это число, умноженное на количество исходных граней, показывает, сколько треугольников будет у нового многогранника.

**ППТ с частотой 8**

Элементы

Количество элементов определяется числом триангуляции ${ displaystyle T = b ^ {2} + bc + c ^ {2}}$ . Два разных геодезических многогранника могут иметь одинаковое количество элементов, например, {3,5+}_5,3 и {3,5+}_7,0 оба имеют T = 49.

Симметрия	Икосаэдр	Восьмигранный	Тетраэдр
Основание	Икосаэдр {3,5} = {3,5+}_1,0	Октаэдр {3,4} = {3,4+}_1,0	Тетраэдр {3,3} = {3,3+}_1,0
Изображение
Символ	{3,5+}_б,c	{3,4+}_б,c	{3,3+}_б,c
Вершины	${ displaystyle 10T + 2}$	${ displaystyle 4T + 2}$	${ displaystyle 2T + 2}$
Лица	${ displaystyle 20T}$	${ displaystyle 8T}$	${ displaystyle 4T}$
Края	${ displaystyle 30T}$	${ displaystyle 12T}$	${ displaystyle 6T}$

Строительство

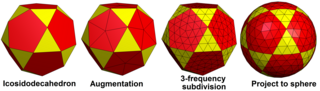
Геодезические многогранники строятся путем разделения граней более простых многогранников и последующего проецирования новых вершин на поверхность сферы. Геодезический многогранник имеет прямые края и плоские грани, которые приближают сферу, но его также можно сделать как сферический многогранник (а мозаика на сфера) с истинным геодезический изогнутые края на поверхности сферы и сферический треугольник лица.

Конвей	ты₃I = (kt) I	(k) tI	ktI
Изображение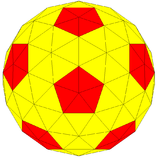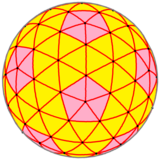
Форма	3-х частотный подразделяется икосаэдр	Кис усеченный икосаэдр	Геодезический многогранник (3,0)	Сферический многогранник

В этом случае {3,5+}_3,0, с частотой ${ displaystyle nu = 3}$ и число триангуляции ${ displaystyle T = 9}$ , каждая из четырех версий многоугольника имеет 92 вершины (80 - при соединении шести ребер и 12 - при соединении пяти), 270 ребер и 180 граней.

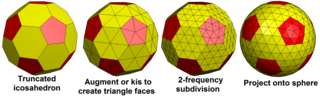
Связь с многогранниками Гольдберга

Геодезические многогранники двойственны многогранникам Гольдберга. Многогранники Гольдберга также связаны тем, что kis оператор (разделение граней на треугольники с помощью центральной точки) создает новые геодезические многогранники, и усечение вершины геодезического многогранника создают новый многогранник Гольдберга. Например, Goldberg G (2,1) целованный, становится {3,5+}_4,1, а усечение становится G (6,3). И аналогично {3,5+}_2,1 усеченный становится G (4,1), и что целованный становится {3,5+}_6,3.

Примеры

I класс

Геодезические многогранники I класса
Частота	(1,0)	(2,0)	(3,0)	(4,0)	(5,0)	(6,0)	(7,0)	(8,0)	(м,0)
Т	1	4	9	16	25	36	49	64	м²
Лицо треугольник									...
Икосаэдр									более
Восьмигранный								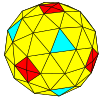	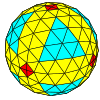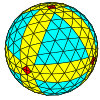более
Тетраэдр									более

II класс

Геодезические многогранники класса II
Частота	(1,1)	(2,2)	(3,3)	(4,4)	(5,5)	(6,6)	(7,7)	(8,8)	(м,м)
Т	3	12	27	48	75	108	147	192	3м²
Лицо треугольник									...
Икосаэдр									более
Восьмигранный									более
Тетраэдр									более

III класс

Геодезические многогранники III класса
Частота	(2,1)	(3,1)	(3,2)	(4,1)	4,2)	(4,3)	(5,1)	(5,2)	(м,п)
Т	7	13	19	21	28	37	31	39	м²+млн+п²
Лицо треугольник									...
Икосаэдр									более
Восьмигранный									более
Тетраэдр									более

Сферические модели

Магнус Веннингеркнига Сферические модели исследует эти подразделения в строительстве модели многогранников. После объяснения конструкции этих моделей он объяснил свое использование треугольных сеток для выделения узоров, при этом треугольники окрашены или исключены в моделях.^[5]

Пример модели
Художественная модель, созданная отцом Магнус Веннингер называется Порядок в хаосе, представляющий киральное подмножество треугольников 16-частотного икосаэдра геодезическая сфера, {3,5+}_16,0	Виртуальная копия, показывающая икосаэдрическая симметрия большие круги. Шестикратная симметрия вращения иллюзорна, не существует на самом икосаэдре.	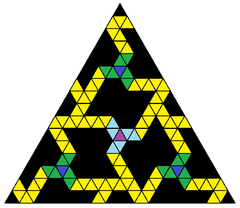Одиночный икосаэдрический треугольник с 16-частным делением