WikiDer > Основа Грёбнера
В математика, а точнее в компьютерная алгебра, вычислительный алгебраическая геометрия, и вычислительные коммутативная алгебра, а Основа Грёбнера это особый вид генераторная установка идеального в кольцо многочленов K[Икс1, ..,Иксп] через поле K. Базис Грёбнера допускает многие важные свойства идеала и связанных с ним алгебраическое многообразие быть легко выведенным, например измерение и количество нулей, когда оно конечно. Вычисление базиса Грёбнера - один из основных практических инструментов решения системы полиномиальных уравнений и вычисление изображений алгебраические многообразия под прогнозы или же рациональные карты.
Вычисление базиса Грёбнера можно рассматривать как многомерное нелинейное обобщение обоих Алгоритм Евклида для вычислений полиномиальные наибольшие общие делители, иГауссово исключение для линейных систем.[1]
Базы Грёбнера были введены в 1965 году вместе с алгоритмом их вычисления (Алгоритм Бухбергера), к Бруно Бухбергер в его докторской степени. Тезис. Он назвал их в честь своего советника Вольфганг Грёбнер. В 2007 году Бухбергер получил Ассоциация вычислительной техникис Премия Пэрис Канеллакис в области теории и практики за эту работу. Однако русский математик Николай Гюнтер ввел аналогичное понятие в 1913 г., опубликованное в различных российских математических журналах. Эти статьи в значительной степени игнорировались математическим сообществом до их повторного открытия в 1987 году Бодо Реншухом. и другие.[2] Аналогичная концепция для многомерного степенной ряд был разработан независимо Хейсуке Хиронака в 1964 году, который назвал их стандартные базы. Некоторые авторы использовали этот термин для обозначения базисов Грёбнера.
Теория базисов Грёбнера развивалась многими авторами в различных направлениях. Он был обобщен на другие структуры, такие как полиномы над кольца главных идеалов или же кольца многочленов, а также некоторые классы некоммутативных колец и алгебр, например Ореалгебры.
Фон
Кольцо полиномов
Базы Грёбнера в первую очередь определены для идеалы в кольцо многочленов через поле K. Хотя теория работает для любого поля, большинство вычислений базиса Грёбнера выполняется либо при K это область рациональных чисел или целые числа по модулю простого числа.
А многочлен это сумма где ненулевые элементы K и находятся мономы или «силовые произведения» переменных. Это означает, что моном M это продукт где неотрицательные целые числа. Вектор называется вектор экспоненты из M. Обозначения часто сокращаются как . Мономы однозначно определяются своими векторами показателей, поэтому компьютеры могут эффективно представлять мономы как векторы показателей, а полиномы - как списки векторов показателей и их коэффициентов.
Если конечный набор многочленов в кольце многочленов р, то идеал, созданный F - множество линейных комбинаций элементов из F с коэффициентами во всех р:
Мономиальный порядок
Все операции, связанные с базами Грёбнера, требуют выбора общий заказ на мономах со следующими свойствами совместимости с умножением. Для всех одночленов M, N, п,
- .
Полный порядок, удовлетворяющий этим условиям, иногда называют допустимый заказ.
Из этих условий следует, что заказ в порядке, т.е. любая строго убывающая последовательность мономов конечна.
Хотя теория базиса Грёбнера не зависит от конкретного выбора допустимого мономиального порядка, три мономиальных порядка особенно важны для приложений:
- Лексикографический порядок, обычно называемый lex или же сплетение (для чисто лексического упорядочивания).
- Общая степень в обратном лексикографическом порядке, обычно называемый дегревлекс.
- Порядок ликвидации, lexdeg.
Теория базиса Грёбнера была первоначально введена для лексикографического упорядочения. Вскоре стало понятно, что базис Грёбнера для degrevlex почти всегда намного проще вычислить, и что почти всегда легче вычислить базис lex-Гребнера, сначала вычислив базис degrevlex, а затем используя «алгоритм изменения порядка». Когда устранение нужен, дегревлекс не удобен; могут использоваться как lex, так и lexdeg, но, опять же, многие вычисления относительно просты с lexdeg и почти невозможны с lex.
Как только мономиальный порядок зафиксирован, термины полинома (произведение одночлена на его ненулевой коэффициент) естественным образом упорядочиваются по убывающим одночленам (для этого порядка). Это делает представление полинома в виде упорядоченного списка пар вектор коэффициента-экспоненты a каноническое представление полиномов. Первый (наибольший) член многочлена п для этого порядка и соответствующие моном и коэффициент называются соответственно ведущий термин, ведущий моном и ведущий коэффициент и обозначается в этой статье как lt (п), лм (п) и lc (п).
Снижение
Концепция чего-либо снижение, также называемый многомерное деление или же нормальная форма вычисление, является центральным в теории базиса Грёбнера. Это многомерное обобщение Евклидово деление одномерных многочленов.
В этом разделе мы предполагаем фиксированный мономиальный порядок, который не будет определяться явно.
Даны два полинома ж и грамм, говорят, что ж является сводимый к грамм если какой-то одночлен м в ж делится на старший моном lm (грамм) из грамм. Если м оказывается главным мономом ж тогда говорят, что ж является свинцовый к грамм. Если c коэффициент при м в ж и м = q лм (грамм), одношаговое сокращение из ж к грамм это операция, которая ассоциируется с ж многочлен
Основные свойства этой операции заключаются в том, что полученный многочлен не содержит одночлена м и что одночлены больше, чем м (для мономиального порядка) остаются без изменений. Эта операция, как правило, не определяется однозначно; если несколько одночленов в ж кратны lm (грамм), то можно произвольно выбрать, какой из них сокращать. На практике для мономиального упорядочения лучше выбрать наибольший, потому что в противном случае последующие редукции могут повторно ввести моном, который был только что удален.
Учитывая конечное множество грамм многочленов, говорят, что ж является сводимый или же свинцовый к грамм если он приводим или приводим соответственно на элемент g из грамм. Если это так, то можно определить . (Полное) сокращение ж к грамм состоит в итеративном применении этого оператора до получения полинома , неприводимое грамм. Это называется нормальная форма из ж к грамм. В общем, эта форма не определена однозначно (это не каноническая форма); эта неединственность является отправной точкой теории базисов Грёбнера.
Для вычислений базиса Грёбнера, за исключением конца, нет необходимости выполнять полную редукцию: сокращение свинца достаточно, что экономит большое количество вычислений.
Из определения редукции сразу видно, что если час это нормальная форма ж к грамм, то имеем
где являются полиномами. В случае одномерных многочленов, если грамм состоит из одного элемента грамм, тогда час остаток от евклидова деления ж к грамм, qграмм - частное, а алгоритм деления - это в точности процесс уменьшения опережения. По этой причине некоторые авторы используют термин многомерное деление вместо сокращения.
Формальное определение
Основа Грёбнера грамм идеального я в кольце многочленов р над полем генераторная установка из я характеризуется любым из следующих свойств, указанных относительно некоторых мономиальный порядок:
- идеал, порожденный главными членами многочленов от я равен идеалу, порожденному главными членами грамм;
- главный член любого многочлена от я делится на главный член некоторого многочлена от грамм;
- то многомерное деление любого многочлена из кольца многочленов р к грамм дает уникальный остаток;
- многомерное деление на грамм любого многочлена от идеала я дает остаток 0.
Все эти свойства эквивалентны; разные авторы используют разные определения в зависимости от выбранной темы. Последние два свойства позволяют проводить вычисления в факторное кольцо R / I с теми же возможностями, что и модульная арифметика. Это знаменательный факт коммутативная алгебра что базисы Грёбнера всегда существуют и могут быть эффективно вычислены для любого идеала, заданного конечным порождающим подмножеством.
Многовариантное деление требует мономиального упорядочения, базис зависит от выбранного мономиального упорядочения, и разные упорядочения могут привести к радикально различным базисам Гребнера. Два наиболее часто используемых порядка: лексикографический порядок, и степень в обратном лексикографическом порядке (также называемый градуированный обратный лексикографический порядок или просто общий порядок получения степени). Лексикографический порядок исключает переменные, однако результирующие базы Грёбнера часто очень велики и дороги в вычислении. Обратный лексикографический порядок степеней обычно обеспечивает самые быстрые вычисления базиса Гребнера. В этом порядке мономы сначала сравниваются по общей степени, а связи разрываются путем взятия наименьшего монома относительно лексикографического упорядочения с измененными переменными.
В большинстве случаев (например, многочлены от конечного числа переменных с комплексными коэффициентами или, в более общем смысле, коэффициенты над любым полем), базисы Грёбнера существуют для любого мономиального порядка. Алгоритм Бухбергера это самый старый и самый известный метод их вычисления. Другие методы - это Алгоритмы Фожера F4 и F5, основанный на той же математике, что и алгоритм Бухбергера, и инволютивные подходы, основанные на идеях из дифференциальная алгебра.[3] Также существует три алгоритма преобразования базиса Грёбнера относительно одного мономиального порядка в базис Грёбнера относительно другого мономиального порядка: Алгоритм FGLM, то Алгоритм, управляемый Гильбертом и Алгоритм прогулки Грёбнера. Эти алгоритмы часто используются для вычисления (сложных) лексикографических базисов Грёбнера из (более простых) базисов Грёбнера полной степени.
Базис Грёбнера называется уменьшенный если старший коэффициент каждого элемента базиса равен 1 и ни один моном в любом элементе базиса не находится в идеале, порожденном старшими членами других элементов базиса. В худшем случае вычисление базиса Гребнера может потребовать экспоненциального или даже экспоненциального времени. дважды экспоненциальный в количестве решений полиномиальной системы (для обратного лексикографического порядка и лексикографического порядка соответственно). Несмотря на эти оценки сложности, как стандартные, так и сокращенные базисы Грёбнера часто вычислимы на практике, и большинство системы компьютерной алгебры содержат процедуры для этого.
Концепция и алгоритмы базисов Грёбнера обобщены на подмодули из бесплатные модули над кольцом многочленов. Фактически, если L свободный модуль над кольцом р, то можно рассмотреть р⊕L как кольцо, определяя произведение двух элементов L равным 0. Это кольцо можно отождествить с куда является основой L. Это позволяет идентифицировать подмодуль L создано с идеалом создано и продукты , . Если р кольцо полиномов, это сводит теорию и алгоритмы базисов Грёбнера модулей к теории и алгоритмам базисов Грёбнера идеалов.
Концепция и алгоритмы базисов Грёбнера также были обобщены на идеалы над различными кольцами, коммутативными или нет, такими как кольца полиномов над кольцом кольцо главных идеалов или же Алгебры Вейля.
Пример и контрпример
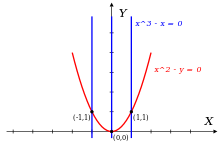
Позволять р = Q[Икс,y] - кольцо двумерных многочленов с рациональными коэффициентами и рассмотрим идеал я = <ж,грамм> порожденные многочленами
- ж(Икс,y) = Икс2 - y
- грамм(Икс,y) = Икс3 - Икс
Два других элемента я многочлены
- k(Икс,y) = -xf(Икс,y) + грамм(Икс,y) = ху - Икс
- час(Икс,y) = xk(Икс,y) − (y - 1)ж(Икс,y) = y2 - y
В лексикографическом порядке с Икс > y у нас есть
- lt (ж) = Икс2
- lt (грамм) = Икс3
- lt (час) = y2
Идеал, порожденный {lt (ж), lt (грамм)} содержит только многочлены, которые делятся на Икс2 который исключает lt (час) = y2; следует, что {ж, грамм} не является базисом Грёбнера для Я.
С другой стороны, можно показать, что {ж, k, час} действительно является базисом Грёбнера для Я.
Во-первых, ж и грамм, и поэтому также h, k а все остальные многочлены в идеале яимеют следующие три нуля в (Икс,y) плоскости, как показано на рисунке: {(1,1), (- 1,1), (0,0)}. Эти три точки не коллинеарны, поэтому я не содержит многочленов первой степени. я содержат любые многочлены специального вида
- м(Икс,y) = сх + п(y)
с c ненулевое рациональное число и п многочлен от переменной y Только; Причина в том, что такая м никогда не может иметь два различных нуля с одинаковым значением для y (в данном случае точки (1,1) и (-1,1)).
Из сказанного выше следует, что Я, помимо нулевого многочлена, содержит только многочлены, старший член которых имеет степень больше или равную 2; поэтому их главные члены делятся хотя бы на один из трех одночленов
- {Икс2, ху, y2} = {lt (ж), lt (k), lt (час)}.
Это означает, что {ж, k, час} является базисом Грёбнера для я относительно лексикографического порядка с Икс > у.
Свойства и применение базисов Грёбнера
Если явно не указано иное, все последующие результаты[4] верны для любого мономиальный порядок (см. в этой статье определения различных порядков, упомянутых ниже).
Распространенное заблуждение, что лексикографический порядок необходим для некоторых из этих результатов. Напротив, лексикографический порядок почти всегда труднее всего вычислить, и его использование делает непрактичными многие вычисления, которые относительно легко выполнить с помощью градуированного обратного лексикографического порядка (grevlex) или, когда необходимо исключение, порядка исключения (lexdeg ), который ограничивается grevlex для каждого блока переменных.
Равенство идеалов
Уменьшенные базы Грёбнера уникальный для любого заданного идеала и любого мономиального порядка. Таким образом, два идеала равны тогда и только тогда, когда они имеют один и тот же (редуцированный) базис Гребнера (обычно программное обеспечение базиса Гребнера всегда производит редуцированные базисы Гребнера).
Членство и включение идеалов
В снижение полинома ж по базису Грёбнера грамм идеального я дает 0 если и только если ж в я. Это позволяет проверить принадлежность элемента к идеалу. Другой метод состоит в проверке того, что базис Грёбнера грамм∪{ж} равно грамм.
Чтобы проверить, идеал ли я создано ж1, ...,жk содержится в идеале J, достаточно проверить, что каждый жя в J. Можно также проверить равенство приведенных базисов Грёбнера J и J∪{ж1, ...,жk}.
Решения системы алгебраических уравнений
Любой набор многочленов можно рассматривать как система полиномиальных уравнений приравняв многочлены нулю. Множество решений такой системы зависит только от сгенерированного идеала и, следовательно, не изменяется при замене данного порождающего набора базисом Гребнера при любом упорядочении сгенерированного идеала. Такое решение с координатами в алгебраически замкнутое поле содержащая коэффициенты полиномов, называется ноль идеала. В обычном случае рациональный коэффициентов, это алгебраически замкнутое поле выбирается в качестве сложное поле.
У идеала нет нуля (система уравнений непоследовательный) тогда и только тогда, когда 1 принадлежит идеалу (это Nullstellensatz Гильберта), или, что то же самое, если его базис Грёбнера (для любого мономиального порядка) содержит 1, или, также, если соответствующий приведенный базис Грёбнера равен [1].
Учитывая базис Грёбнера грамм идеального я, он имеет только конечное число нулей тогда и только тогда, когда для каждой переменной Икс, грамм содержит многочлен со старшим одночленом, являющимся степенью Икс (без каких-либо других переменных, появляющихся в ведущем члене). Если это так, количество нулей, подсчитанных с кратностью, равно количеству одночленов, не кратных любому старшему одночлену из грамм. Этот номер называется степень идеала.
Когда число нулей конечно, базис Грёбнера для лексикографического мономиального упорядочения теоретически обеспечивает решение: первые координаты решения являются корнем наибольший общий делитель полиномов базиса, зависящего только от первой переменной. После подстановки этого корня в базис вторые координаты этого решения являются корнем наибольшего общего делителя полученных многочленов, который зависит только от этой второй переменной, и так далее. Этот процесс решения является только теоретическим, поскольку он подразумевает вычисление НОД и нахождение корня многочленов с приближенными коэффициентами, что невозможно из-за числовой нестабильности. Поэтому были разработаны другие методы решения полиномиальных систем через базисы Грёбнера (см. Система полиномиальных уравнений Больше подробностей).
Размерность, степень и ряд Гильберта
В измерение идеального я в кольце многочленов р это Измерение Крулля кольца р/я и равен размерность алгебраического множества нулей я. Это также равно количеству гиперплоскости в общая позиция которые необходимы для пересечения с алгебраическим множеством, которое представляет собой конечное число точек. В степень идеала и связанного с ним алгебраического множества есть количество точек этого конечного пересечения, считаемое с кратностью. В частности, степень гиперповерхность равна степени его полинома определения.
И степень, и размерность зависят только от набора главных мономов базиса Грёбнера идеала для любого мономиального порядка.
Размерность - это максимальный размер подмножества S переменных таких, что нет старшего монома, зависящего только от переменных в S. Таким образом, если идеал имеет размерность 0, то для каждой переменной Икс в базисе Грёбнера есть старший моном, являющийся степенью Икс.
И размер, и степень могут быть выведены из Ряд Гильберта идеала, который представляет собой серию , куда - количество одночленов степени я которые не кратны никакому старшему одночлену в базисе Грёбнера. Ряд Гильберта можно суммировать в рациональную дробь
куда d размер идеала и - многочлен такой, что степень идеальности.
Хотя размерность и степень не зависят от выбора мономиального порядка, ряд Гильберта и многочлен изменяется при изменении мономиального порядка.
Наиболее системы компьютерной алгебры которые предоставляют функции для вычисления базисов Грёбнера, предоставляют также функции для вычисления ряда Гильберта и, следовательно, также размерности и степени.
Устранение
Вычисление базисов Грёбнера для устранение мономиальный порядок позволяет вычислить теория исключения. Это основано на следующей теореме.
Рассмотрим кольцо многочленов в котором переменные разбиты на два подмножества Икс и Y. Выберем также элиминационный мономиальный порядок «исключающий» Икс, то есть мономиальный порядок, для которого сравниваются два монома, сравнивая сначала Икс-частей, и, только в случае равенства, учитывая Y-части. Отсюда следует, что моном, содержащий Икс-переменная больше любого одночлена, не зависящего от Икс.Если грамм является базисом Грёбнера идеала я для этого мономиального порядка является базисом Грёбнера (этот идеал часто называют исключение идеал). Более того, состоит в точности из полиномов от грамм чьи ведущие термины принадлежат K[Y] (это очень упрощает вычисление , так как нужно проверять только ведущие одночлены).
Этот свойство исключения имеет множество приложений, о некоторых из них мы расскажем в следующих разделах.
Другое приложение, в алгебраическая геометрия, в том, что устранение реализует геометрическую операцию проекция из аффинное алгебраическое множество в подпространство окружающего пространства: с указанными выше обозначениями (Зариски закрытие из) проекция алгебраического множества, определяемая идеалом я в Y-подпространство определяется идеалом
Лексикографический порядок такой, что порядок исключения для каждого раздела Таким образом, основа Грёбнера для этого упорядочивания содержит гораздо больше информации, чем обычно необходимо. Это может объяснить, почему основы Гребнера для лексикографического упорядочения обычно труднее всего вычислить.
Пересекающиеся идеалы
Если я и J два идеала, порожденные соответственно {ж1, ..., жм}и {грамм1, ..., граммk}, то одно вычисление базиса Грёбнера дает базис Грёбнера их пересечения я ∩ J. Для этого вводится новый неопределенный т, и один использует порядок исключения, так что первый блок содержит только т а другой блок содержит все остальные переменные (это означает, что моном, содержащий т больше любого одночлена, не содержащего т). При таком мономиальном порядке базис Грёбнера я ∩ J состоит из полиномов, не содержащих т, в базисе Грёбнера идеального
Другими словами, я ∩ J получается устранение т в KЭто можно доказать, заметив, что идеальный K состоит из полиномов такой, что и . Такой многочлен не зависит от т если и только а=б, что обозначает
Неявное отображение рациональной кривой
А рациональная кривая является алгебраическая кривая что есть параметрическое уравнение формы
куда и являются одномерными многочленами при 1 ≤ я ≤ п. Можно (и будет) предположить, что и находятся совмещать (у них нет непостоянных общих факторов).
Неявная реализация состоит в вычислении неявные уравнения такой кривой. В случае п = 2, то есть для плоских кривых, это можно вычислить с помощью результирующий. Неявное уравнение имеет следующий результат:
Исключение с базисами Грёбнера позволяет неявно определять для любого значения п, просто исключив т в идеалеЕсли п = 2, результат такой же, как и с результирующим, если отображение инъективен почти для всех т. В другом случае результат - это степень результата исключения.
Насыщенность
При моделировании проблемы с помощью полиномиальных уравнений очень часто предполагается, что некоторые величины не равны нулю, потому что, если они равны нулю, проблема становится совсем другой. Например, при работе с треугольники, многие свойства становятся ложными, если треугольник вырожден, то есть если длина одной стороны равна сумме длин других сторон. В таких ситуациях нет никакой надежды на получение релевантной информации из полиномиальной системы, если вырожденные решения не выпадают. Точнее, система уравнений определяет алгебраический набор который может иметь несколько неприводимые компоненты, и нужно удалить компоненты, на которых условия вырождения всюду равны нулю.
Это делается насыщающий уравнения по условиям вырождения, что можно сделать, используя свойство исключения базисов Грёбнера.
Определение насыщенности
В локализация кольца состоит в присоединении к нему формальных инверсий некоторых элементов. Этот раздел касается только случая одного элемента или, что то же самое, конечного числа элементов (соединение обратных элементов нескольких элементов эквивалентно соединению обратных элементов их произведения). В локализация кольца р элементом ж кольцо куда т является новым неопределенным, представляющим инверсию ж. В локализация идеального я из р это идеал из Когда р кольцо многочленов, вычисляющее в неэффективен из-за необходимости управлять знаменателями. Следовательно, работа локализация обычно заменяется операцией насыщенность.
В насыщенность относительно ж идеального я в р это прообраз под канонической картой из р к Это идеал состоящий из всех элементов р чьи продукты в силу некоторой ж принадлежит я.
Если J идеал, порожденный я и 1-футов в р[т], тогда Отсюда следует, что если р кольцо многочленов, вычисление базиса Грёбнера исключает т позволяет вычислить базис Грёбнера насыщения идеала полиномом.
Важное свойство насыщенности, которое гарантирует, что оно удаляет из алгебраического множества, определяемого идеалом я то неприводимые компоненты на котором многочлен ж равен нулю, это следующее: В первичное разложение из состоит из компонентов примарного разложения I, не содержащих никакой степени f.
Расчет насыщенности
Базис Грёбнера насыщения ж полиномиального идеала, порожденного конечным набором многочленов F, можно получить, исключив т в то есть сохраняя полиномы независимыми от т в базисе Грёбнера для устранения заказа устранения т.
Вместо того, чтобы использовать F, можно также исходить из базиса Грёбнера F. Какой метод наиболее эффективен, зависит от проблемы. Однако, если насыщение не удаляет какой-либо компонент, то есть если идеал равен его насыщенному идеалу, сначала вычисляется базис Гребнера F обычно быстрее. С другой стороны, если насыщение удаляет некоторые компоненты, прямое вычисление может быть значительно быстрее.
Если вы хотите насытить по нескольким полиномам или относительно одного полинома, который является произведением есть три способа продолжить, которые дают один и тот же результат, но могут иметь очень разное время вычисления (это зависит от проблемы, которая является наиболее эффективной).
- Насыщение в одном вычислении базиса Грёбнера.
- Насыщение затем насыщая результат и так далее.
- Добавление к F или его базису Грёбнера многочлены и устранение в одном вычислении базиса Грёбнера.
Эффективный Nullstellensatz
Nullstellensatz Гильберта есть две версии. Первый утверждает, что набор многочленов имеет пустой набор общих нулей в алгебраическое замыкание поля коэффициентов тогда и только тогда, когда 1 принадлежит порожденному идеалу. Это легко проверить с помощью вычисления базиса Грёбнера, потому что 1 принадлежит идеалу тогда и только тогда, когда 1 принадлежит базису Грёбнера идеала для любого мономиального порядка.
Вторая версия утверждает, что множество общих нулей (в алгебраическом замыкании поля коэффициентов) идеала содержится в гиперповерхность нулей полинома ж, тогда и только тогда, когда степень ж принадлежит к идеалу. Это можно проверить, пропитав идеал ж; на самом деле, сила ж принадлежит идеалу тогда и только тогда, когда насыщенность ж дает базис Грёбнера, содержащий 1.
Неявная реализация в более высоком измерении
По определению аффинная рациональное разнообразие измерения k может быть описан параметрические уравнения формы
куда находятся п+1 многочлен от k переменные (параметры параметризации) Таким образом, параметры и координаты точек многообразия - нули идеального
Можно было догадаться, что для получения неявных уравнений многообразия достаточно исключить параметры, как это было сделано в случае кривых. К сожалению, это не всегда так. Если имеют общий ноль (иногда называемый базовая точка), каждый неприводимая составляющая непустого алгебраического множества, определяемого - неприводимая компонента алгебраического множества, определяемого формулой я. Отсюда следует, что в этом случае прямое устранение предоставляет пустой набор многочленов.
Следовательно, если k> 1, необходимы два вычисления базиса Гребнера для неявного выражения:
- Насыщать к получить основу Грёбнера
- Устранить из получить базис Грёбнера идеала (неявных уравнений) многообразия.
Реализации
- Какао бесплатная система компьютерной алгебры для вычисления базисов Грёбнера.
- ЗАЗОР бесплатная система компьютерной алгебры, которая может выполнять вычисления базисов Грёбнера.
- FGb, собственная реализация Фогера его Алгоритм F4, доступный как Клен библиотека.[5] На сегодняшний день, по состоянию на 2014 год, с Magma это самая быстрая реализация рациональных коэффициентов и коэффициентов в конечном поле простого порядка.
- Маколей 2 бесплатное программное обеспечение для выполнения полиномиальных вычислений, в частности вычислений базиса Гребнера.
- Магма имеет очень быструю реализацию алгоритма F4 Фожера.[6]
- Клен имеет реализации алгоритмов Бухбергера и Фогера F4, а также трассировку Грёбнера.
- Mathematica включает в себя реализацию алгоритма Бухбергера с такими методами повышения производительности, как обход Гребнера, след Гребнера и улучшение торических оснований.
- ЕДИНСТВЕННОЕ ЧИСЛО бесплатное программное обеспечение для вычисления коммутативных и некоммутативных базисов Гребнера.
- SageMath предоставляет унифицированный интерфейс для нескольких систем компьютерной алгебры (включая SINGULAR и Macaulay) и включает несколько собственных базовых алгоритмов Гребнера.
- SymPy Система компьютерной алгебры Python использует базисы Грёбнера для решения полиномиальных систем.
Области применения
Коды с исправлением ошибок
Базис Грёбнера был применен в теории кодов с исправлением ошибок для алгебраического декодирования. Используя вычисление базиса Грёбнера на различных формах уравнений с исправлением ошибок, были разработаны методы декодирования для исправления ошибок циклических кодов,[7] аффинные коды разновидностей,[8] алгебро-геометрические коды и даже общие линейные блочные коды.[9] Применение базиса Грёбнера в алгебраическом декодировании по-прежнему является областью исследований теории канального кодирования.
Смотрите также
- Алгоритм Бухбергера
- Алгоритмы Фожера F4 и F5
- Основание Graver
- Основа Джанет
- Обычные цепи, альтернативный способ представления алгебраических множеств
Рекомендации
- ^ Лазард, Даниэль (1983). «Базисы Грёбнера, исключение Гаусса и разрешение систем алгебраических уравнений». Компьютерная алгебра. Конспект лекций по информатике. 162. С. 146–156. Дои:10.1007/3-540-12868-9_99. ISBN 978-3-540-12868-7.
- ^ Бодо Реншух, Хартмут Ролофф, Георгий Г. Распутин и др. al. (2003). Вклад в конструктивную теорию полиномиальных идеалов XXIII: забытые работы ленинградского математика Н. М. Гюнтера по теории полиномиальных идеалов. Бюллетень ACM SIGSAM, Том 37, № 2, (2003): 35–48. Английский перевод Майкла Абрамсона.
- ^ Владимир П. Гердт, Юрий А. Блинков (1998). Инволютивные базисы полиномиальных идеалов, Математика и компьютеры в моделировании, 45: 519ff
- ^ Кокс, Дэвид А.; Литтл, Джон; О'Ши, Донал (1997). Идеалы, многообразия и алгоритмы: введение в вычислительную алгебраическую геометрию и коммутативную алгебру. Springer. ISBN 0-387-94680-2.
- ^ Домашняя страница FGb
- ^ Страница хронометража Грёбнера Allan Steel
- ^ X. Chen, I.S. Рид, Т. Хеллесет и Т.К. Чыонг (1994). «Использование баз Гребнера для декодирования двоичных циклических кодов до истинного минимального расстояния», - IEEE Trans. Сообщить. Теория, т. ИТ-40, с. 1654-1661.
- ^ Дж. Фитцджеральд, Р.Ф. Лакс, (1998). «Декодирование аффинных кодов разновидностей с использованием баз Грёбнера», Designs, Codes and Cryptography, vol. 13. С. 147–158.
- ^ С. Булыгин, Р. Пелликаан (2009). Декодирование линейных кодов с исправлением ошибок до половины минимального расстояния с помощью баз Гребнера, баз Гребнера, кодирования и криптографии, Springer-Verlag Berlin Heidelberg, стр. 361–365.ISBN 978-3-540-93805-7
дальнейшее чтение
- Уильям У. Адамс, Филипп Лустонау (1994). Введение в основы Грёбнера. Американское математическое общество, Аспирантура по математике, Том 3. ISBN 0-8218-3804-0
- Хуиши Ли (2011). Основы Грёбнера в теории колец. Мировое научное издательство, ISBN 978-981-4365-13-0
- Томас Беккер, Фолькер Вайспфеннинг (1998). Базы Грёбнера. Тексты для выпускников Springer по математике 141. ISBN 0-387-97971-9
- Бруно Бухбергер (1965). Алгоритм нахождения базисных элементов кольца классов вычетов нульмерного полиномиального идеала. Кандидат наук. докторскую диссертацию, Инсбрукский университет. Английский перевод Майкла Абрамсона в Журнал символических вычислений 41 (2006): 471–511. [Это тезис Бухбергера об изобретении основ Грёбнера.]
- Бруно Бухбергер (1970). Алгоритмический критерий разрешимости системы алгебраических уравнений. Aequationes Mathematicae 4 (1970): 374–383. Английский перевод Майкла Абрамсона и Роберта Ламберта в Основы Грёбнера и приложения (Б. Бухбергер, Ф. Винклер, ред.). Серия лекций Лондонского математического общества 251, Cambridge University Press, 1998, 535–545. ISBN 0-521-63298-6 (Это журнальная публикация диссертации Бухбергера.)
- Бухбергер, Бруно; Кауэрс, Мануэль (2010). «Базы Грёбнера». Scholarpedia (5): 7763. Дои:10.4249 / scholarpedia.7763.
- Ральф Фрёберг (1997). Введение в основы Грёбнера. Wiley & Sons. ISBN 0-471-97442-0.
- Штурмфельс, Бернд (Ноябрь 2005 г.), "Что такое ... Основа Грёбнера?" (PDF), Уведомления Американского математического общества, 52 (10): 1199–1200, краткое введение.
- Ширшов, Анатолий И. (1999). «Некоторые алгоритмические проблемы для алгебр Ли» (PDF). Бюллетень ACM SIGSAM. 33 (2): 3–6. Дои:10.1145/334714.334715. (translated from Sibirsk. Mat. Zh. Siberian Mathematics Journal 3 (1962), 292–296).
- Matthias Aschenbrenner and Christopher Hillar, Finite generation of symmetric ideals, Труды Американского математического общества 359 (2007), no. 11, 5171–5192 (on infinite dimensional Gröbner bases for polynomial rings in infinitely many indeterminates).
внешняя ссылка
- Faugère's own implementation of his F4 algorithm
- "Gröbner basis", Энциклопедия математики, EMS Press, 2001 [1994]
- B. Buchberger, Gröbner Bases: A Short Introduction for Systems Theorists в Proceedings of EUROCAST 2001.
- Buchberger, B. and Zapletal, A. Gröbner Bases Bibliography.
- Comparative Timings Page for Gröbner Bases Software
- Prof. Bruno Buchberger Бруно Бухбергер
- Вайсштейн, Эрик В. "Gröbner Basis". MathWorld.
- Gröbner basis introduction на Scholarpedia
![R=K[x_1,ldots,x_n]](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c260b0a6d62c47a5e1a795e82e3e5880d8fbb02)





![A=[a_1, ldots ,a_n]](https://wikimedia.org/api/rest_v1/media/math/render/svg/2513a388469f481f5005e914fbfa3c75d62b8738)


![langle f_1,ldots, f_k
angle = left{sum_{i=1}^k g_i f_i;|; g_1,ldots, g_kin K[x_1,ldots,x_n]
ight}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/d58dcf0954935af39f4dc2f6c48e532bdf819c72)








![R[e_1, ldots, e_l]/leftlangle {e_ie_j|1le ile jle l}
ight
angle,](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee1cf7a72a54d87bf8a5cb6d8ddf156c39d9eed2)


![R[e_1, ldots, e_l]](https://wikimedia.org/api/rest_v1/media/math/render/svg/39543a673a78c16fbe797f637a2393dfc4acc53d)







![K[x_1,ldots,x_n,y_1,ldots,y_m]=K[X,Y],](https://wikimedia.org/api/rest_v1/media/math/render/svg/81076bdd41f515dd5c808ab2ea163b93ce4cce30)
![Gcap K[Y]](https://wikimedia.org/api/rest_v1/media/math/render/svg/044dda005cf6d35268673c93a816ce678082e99b)
![Icap K[Y]](https://wikimedia.org/api/rest_v1/media/math/render/svg/04e68e6bbb055caa519acd51afcfa529c587cb94)
![Icap K[Y].](https://wikimedia.org/api/rest_v1/media/math/render/svg/c39554734c07f68f1f094f9fbb2d4c4d33dbd430)













![R_f=R[t]/(1-ft),](https://wikimedia.org/api/rest_v1/media/math/render/svg/8713e05438bdd8e7bbb45a04021121168c2b01db)
























