WikiDer > Большой звездчатый 120-элементный

Great grand stellated 120-cell
Большой звездчатый 120-элементный
Орто массив 016-однородный полихорон p33-t0.png
Ортогональная проекция
ТипПолихорон Шлефли-Гесса
Клетки120 {5/2,3}
Лица720 {5/2}
Края1200
Вершины600
Фигура вершины{3,3}
Символ Шлефли{5/2,3,3}
Диаграмма Кокстера-ДынкинаCDel node 1.pngCDel 5.pngCDel rat.pngCDel d2.pngCDel node.pngCDel 3.pngCDel node.pngCDel 3.pngCDel node.png
Группа симметрииЧАС4, [3,3,5]
ДвойнойГранд 600-секционный
ХарактеристикиОбычный
А Zome модель

В геометрия, то большой звездчатый 120-элементный или же большой звездчатый полидодекаэдр это правильный звездный 4-многогранник с Символ Шлефли {5 / 2,3,3}, один из 10 правильных 4-многогранников Шлефли-Гесса. Он уникален среди 10, поскольку имеет 600 вершин и имеет такое же расположение вершин как правильная выпуклая 120 ячеек.

Это один из четырех правильная звездчатая полихора обнаружен Людвиг Шлефли. Он назван Джон Хортон Конвей, расширяя систему именования Артур Кэли для Твердые тела Кеплера-Пуансо, и единственный, содержащий все три модификатора в имени.

Благодаря своей двойственности он образует соединение великих звёздчатых 120-ячеечных и 600-ячеечных.

Изображений

Изображения самолета Кокстера
ЧАС4А2 / B3А3 / B2
Большой звездчатый 120-элементный, {5 / 2,3,3}
Большой звездчатый 120-cell-ortho-10gon.pngБольшой звездчатый 120-cell-6gon.pngБольшой звездчатый 120-cell-4gon.png
[10][6][4]
120 ячеек, {5,3,3}
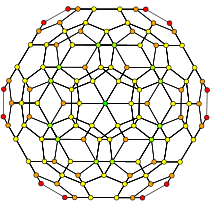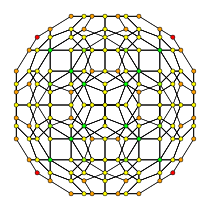120-элементный t0 H3.svg120-элементный t0 A2.svg120-элементный t0 A3.svg

Как звездочка

В большой звездчатый 120-элементный это окончательный звездчатость из 120 ячеек, и это единственный полихорон Шлефли-Гесса, имеющий 120-клеточную выпуклую оболочку. В этом смысле он аналогичен трехмерному большой звездчатый додекаэдр, которая является последней звездочкой додекаэдр и единственный многогранник Кеплера-Пуансо, имеющий додекаэдр в качестве выпуклой оболочки. Действительно, великая звездчатая 120-ячеечная система двойственна большой 600-элементный, который можно было бы принять как 4D аналог большой икосаэдр, двойственный к большому звездчатому додекаэдру.

Края большой звездчатой ​​120-элементной τ6 до тех пор, пока клетки ядра из 120 клеток находятся глубоко внутри полихорона, и они равны τ3 пока те из маленький звездчатый 120-элементный глубоко внутри полихорона.

Смотрите также

Рекомендации

  • Эдмунд Гесс, (1883) Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder [1].
  • Х. С. М. Коксетер, Правильные многогранники, 3-й. изд., Dover Publications, 1973. ISBN 0-486-61480-8.
  • Джон Х. Конвей, Хайди Берджель, Хаим Гудман-Штрасс, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 26, Правильные звездные многогранники, стр. 404–408)
  • Клитцинг, Ричард. "4D однородные многогранники (полихоры) o3o3o5 / 2x - гогиши".

внешняя ссылка

Фундаментальный выпуклый обычный и однородные многогранники в размерах 2–10
СемьяАпBпя2(п) / DпE6 / E7 / E8 / F4 / грамм2ЧАСп
Правильный многоугольникТреугольникКвадратп-угольникШестиугольникПентагон
Равномерный многогранникТетраэдрОктаэдр • КубДемикубДодекаэдр • Икосаэдр
Равномерный 4-многогранник5-элементный16 ячеек • ТессерактDemitesseract24-элементный120 ячеек • 600 ячеек
Равномерный 5-многогранник5-симплекс5-ортоплекс • 5-куб5-полукуб
Равномерный 6-многогранник6-симплекс6-ортоплекс • 6-куб6-полукуб122 • 221
Равномерный 7-многогранник7-симплекс7-ортоплекс • 7-куб7-полукуб132 • 231 • 321
Равномерный 8-многогранник8-симплекс8-ортоплекс • 8-куб8-полукруглый142 • 241 • 421
Равномерный 9-многогранник9-симплекс9-ортоплекс • 9-куб9-полукруглый
Равномерный 10-многогранник10-симплекс10-ортоплекс • 10-куб10-полукуб
Униформа п-многогранникп-симплексп-ортоплекс • п-кубп-полукуб1k2 • 2k1 • k21п-пятиугольный многогранник
Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений