WikiDer > Равномерный многогранник
Эта статья может быть сбивает с толку или неясно читателям. (Сентябрь 2008 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
| 2D | 3D |
|---|---|
 Усеченный треугольник или униформа шестиугольник, с Диаграмма Кокстера |  Усеченный октаэдр, |
| 4D | 5D |
 Усеченная 16-ячеечная, |  Усеченный 5-ортоплекс, |
А равномерный многогранник размерности три или выше является вершинно-транзитивный многогранник ограниченный униформой грани. Однородные многогранники в двух измерениях - это правильные многоугольники (определение отличается в двух измерениях, чтобы исключить транзитивные по вершинам четные многоугольники, у которых чередуются две разные длины ребер).
Это обобщение более старой категории полуправильный многогранники, но также включает правильные многогранники. Дальше, звезда регулярный лица и фигуры вершин (звездные многоугольники), что значительно расширяет возможные решения. Строгое определение требует, чтобы однородные многогранники были конечными, в то время как более широкое определение позволяет однородные соты (2-мерный мозаики и более высокие измерения соты) из Евклидово и гиперболическое пространство также считаться многогранниками.
Операции
Почти каждый равномерный многогранник может быть порожден Строительство Wythoff, и представлен Диаграмма Кокстера. Известные исключения включают большой диромбикосододекаэдр в трех измерениях и великая антипризма в четырех измерениях. Терминология выпуклых равномерных многогранников, используемая в равномерный многогранник, равномерный 4-многогранник, равномерный 5-многогранник, равномерный 6-многогранник, равномерная черепица, и выпуклые однородные соты статьи были придуманы Норман Джонсон.[нужна цитата]
Эквивалентно, многогранники Витоффа могут быть сгенерированы путем применения основных операций к правильным многогранникам в этом измерении. Этот подход был впервые использован Иоганн Кеплер, и является основой Обозначения многогранника Конвея.
Операторы ректификации
Правильные n-многогранники имеют п заказы исправление. Нулевое исправление - это исходная форма. (п−1) -ое выпрямление двойной. А исправление сводит ребра к вершинам, a двунаправленная связь сводит грани к вершинам, a триректификация сводит клетки к вершинам, a квадратификация сводит 4-грани к вершинам, a квинтиректификация свел 5-граней к вершинам и так далее.
Расширенный Символ Шлефли может использоваться для представления исправленных форм с одним нижним индексом:
- k-я ректификация = тk{п1, п2, ..., пп-1} = kр.
Операторы усечения
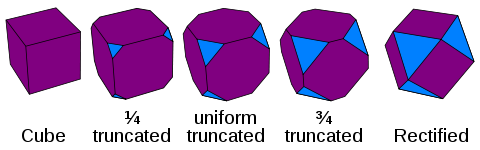
Операции усечения, которые можно применить к обычным п-политопы в любом сочетании. Результирующая диаграмма Кокстера имеет два окруженных кольцом узла, и операция названа в честь расстояния между ними. Усечение разрезает вершины, песня режет края, бегство режет лица, стерилизация вырезать клетки. Каждая более высокая операция также обрезает и более низкие, поэтому канелляция также обрезает вершины.
- т0,1 или же т: Усечение - применительно к полигоны и выше. Усечение удаляет вершины и вставляет новый фасет вместо каждой предыдущей вершины. Грани усекаются, их края удваиваются. (Термин, введенный Кеплер, происходит от латинского truncare 'отрезать'.)
- Также есть высшие усечения: битовое усечение т1,2 или же 2т, усечение т2,3 или же 3т, квадроусечение т3,4 или же 4т, пятикратное усечение т4,5 или же 5т, так далее.
- т0,2 или же rr: Cantellation - применительно к многогранники и выше. Это можно рассматривать как исправление исправление. Кантелляция обрезает и вершины, и ребра и заменяет их новыми фасетами. Ячейки заменены на топологически расширенный копии самих себя. (Термин, придуманный Джонсоном, происходит от глагола косяк, подобно скос, то есть резать с наклонным лицом.)
- Есть и более высокие песнопения: двухстороннее созвездие т1,3 или же r2r, трикантелляция т2,4 или же r3r, квадрикозвездие т3,5 или же r4r, так далее.
- т0,1,2 или же tr: Cantitruncation - применительно к многогранники и выше. Это можно рассматривать как усечение исправление. Кантусечение обрезает и вершины, и ребра и заменяет их новыми фасетами. Ячейки заменены на топологически расширенный копии самих себя. (Составной термин объединяет канелляцию и усечение)
- Есть и более высокие песнопения: двунаправленное усечение т1,2,3 или же t2r, трехслойное усечение т2,3,4 или же t3r, четырехугольник т3,4,5 или же t4r, так далее.
- т0,3: Runcination - применительно к Равномерный 4-многогранник и выше. Runcination усекает вершины, ребра и грани, заменяя их каждой новой гранью. 4-грани заменяются топологически расширенными копиями самих себя. (Термин, введенный Джонсоном, происходит от латинского Runcina 'плотник самолет'.)
- Также существуют более высокие уровни: бирунцирование т1,4, усечение т2,5, так далее.
- т0,4 или же 2r2r: Стерилизация - применительно к Равномерные 5-многогранники и выше. Это можно рассматривать как биректификацию своей биректификации. Стерилизация обрезает вершины, ребра, грани и ячейки, заменяя их новыми фасетами. 5-грани заменяются топологически расширенными копиями самих себя. (Термин, введенный Джонсоном, происходит от греческого стереосистемы 'твердый'.)
- Также существуют более высокие стерилизации: бистерификация т1,5 или же 2r3r, тристерикация т2,6 или же 2r4r, так далее.
- т0,2,4 или же 2т2р: Stericantellation - применительно к Равномерные 5-многогранники и выше. Это можно рассматривать как сокращение его двунаправленной адресации.
- Также существуют более высокие стерилизации: бистериканское созвездие т1,3,5 или же 2т3р, трехстороннее созвездие т2,4,6 или же 2т4р, так далее.
- т0,5: Pentellation - применительно к Равномерные 6-многогранники и выше. Pentellation обрезает вершины, ребра, грани, ячейки и 4-грани, заменяя каждую новую грань. 6-гранки заменяются топологически расширенными копиями самих себя. (Pentellation происходит от греческого Pente 'пять'.)
- Существуют также более высокие пентеллы: двойное зрение т1,6, тройное созвездие т2,7, так далее.
- т0,6 или же 3r3r: Проклятие - применительно к Равномерные 7-многогранники и выше. Его можно рассматривать как триректификацию. Hexication усекает вершины, ребра, грани, ячейки, 4-грани и 5-грани, заменяя их новыми гранями. 7-грани заменяются топологически расширенными копиями самих себя. (Hexication происходит от греческого шестнадцатеричный 'шесть'.)
- Также существуют высшие отравления: бигексикация: т1,7 или же 3r4r, тригексикация: т2,8 или же 3r5r, так далее.
- т0,3,6 или же 3т3р: Гексирунцинированный - применительно к Равномерные 7-многогранники и выше. Это можно рассматривать как сокращение его триректификации.
- Также существуют высшие гексирунции: бигексирунцинированный: т1,4,7 или же 3t4r, тригексирунцинированный: т2,5,8 или же 3т5р, так далее.
- т0,7: Heptellation - применительно к Равномерные 8-многогранники и выше. Heptellation усекает вершины, ребра, грани, ячейки, 4-грани, 5-грани и 6-грани, заменяя каждую грань новыми гранями. 8-грани заменяются топологически расширенными копиями самих себя. (Heptellation происходит от греческого гепта 'Семь'.)
- Также есть высшие звёзды: бигептелляция т1,8, Triheptellation т2,9, так далее.
- т0,8 или же 4r4r: Octellation - применительно к Равномерные 9-многогранники и выше.
- т0,9: Ennecation - применительно к Равномерные 10-многогранники и выше.
Кроме того, могут выполняться комбинации усечений, которые также генерируют новые однородные многогранники. Например, runcitruncation это бегство и усечение применяется вместе.
Если все усечения применяются одновременно, операцию можно в более общем виде назвать омниусечение.
Чередование
Одна специальная операция, называемая чередование, удаляет альтернативные вершины из многогранника, имеющего только четные грани. Альтернативный всесторонне усеченный многогранник называется пренебрежительно.
Результирующие многогранники всегда можно построить, и они, как правило, не являются отражающими, а также не имеют униформа решения многогранников.
Набор многогранников, образованных чередованием гиперкубы известны как полукубы. В трех измерениях это дает тетраэдр; в четырех измерениях это дает 16 ячеек, или же demitesseract.
Фигура вершины
Равномерные многогранники можно построить из их вершина фигуры, расположение ребер, граней, ячеек и т.д. вокруг каждой вершины. Равномерные многогранники, представленные Диаграмма Кокстера, маркирующие активные зеркала кольцами, обладают отражательной симметрией и могут быть просто построены рекурсивным отражением фигуры вершины.
Меньшее количество неотражающих однородных многогранников имеет единственную вершинную фигуру, но не повторяется простыми отражениями. Большинство из них можно представить с помощью таких операций, как чередование других равномерных многогранников.
Фигуры вершин для диаграмм Кокстера с одним кольцом могут быть построены из диаграммы путем удаления узла с кольцом и вызова соседних узлов. Такие вершинные фигуры сами по себе вершинно-транзитивны.
Многогранники с кольцами могут быть построены несколько более сложным процессом построения, и их топология не является однородным многогранником. Например, фигура вершины усеченный правильный многогранник (с двумя кольцами) - пирамида. An всесторонне усеченный многогранник (все узлы окольцованы) всегда будет иметь неправильный симплекс как фигура его вершины.
Circumradius
Равномерные многогранники имеют равные длины ребер, а все вершины находятся на одинаковом расстоянии от центра, называемом по окружности.
Однородные многогранники, радиус описанной окружности которых равен длине ребра, можно использовать как фигуры вершин за однородные соты. Например, обычный шестиугольник делится на 6 равносторонних треугольников и является фигурой вершины правильного треугольная черепица. Так же кубооктаэдр делится на 8 правильных тетраэдров и 6 квадратных пирамид (половина октаэдр), и это фигура вершины для чередующиеся кубические соты.
Равномерные многогранники по размерности
Полезно классифицировать однородные многогранники по размерности. Это эквивалентно количеству узлов на диаграмме Кокстера или количеству гиперплоскостей в конструкции Витхоффа. Потому что (п+1) -мерные многогранники являются мозаиками п-мерное сферическое пространство, мозаики п-размерный Евклидово и гиперболическое пространство также считаются (п+1) -мерный. Следовательно, мозаики двумерного пространства группируются с трехмерными телами.
Одно измерение
Единственный одномерный многогранник - это отрезок прямой. Он соответствует семейству Кокстера A1.
Два измерения
В двух измерениях существует бесконечное семейство выпуклых равномерных многогранников. правильные многоугольники, самый простой из которых - равносторонний треугольник. Усеченные правильные многоугольники становятся двухцветными геометрически квазирегулярный многоугольники с вдвое большим числом сторон, t {p} = {2p}. Ниже показаны первые несколько правильных многоугольников (и квазирегулярных форм):
| Имя | Треугольник (2-симплекс) | Квадрат (2-ортоплекс) (2-куб) | Пентагон | Шестиугольник | Семиугольник | Восьмиугольник | Девятиугольник | Декагон | Hendecagon |
|---|---|---|---|---|---|---|---|---|---|
| Schläfli | {3} | {4} т {2} | {5} | {6} т {3} | {7} | {8} т {4} | {9} | {10} т {5} | {11} |
| Coxeter диаграмма | |||||||||
| Изображение |  |   |  |   |  |   |  |   |  |
| Имя | Додекагон | Трехугольник | Тетрадекагон | Пентадекагон | Шестиугольник | Гептадекагон | Восьмиугольник | Enneadecagon | Икосагон |
| Schläfli | {12} т {6} | {13} | {14} т {7} | {15} | {16} т {8} | {17} | {18} т {9} | {19} | {20} т {10} |
| Coxeter диаграмма | |||||||||
| Изображение |   |  |   |  |   |  |   |  |   |
Также существует бесконечный набор звездные многоугольники (по одному на каждый Рациональное число больше 2), но они невыпуклые. Самый простой пример - это пентаграмма, что соответствует рациональному числу 5/2. Правильные звездчатые многоугольники {p / q} могут быть усечены до полуправильных звездных многоугольников t {p / q} = t {2p / q}, но становятся двойными покрытиями, если q даже. Усечение также может быть выполнено с помощью многоугольника обратной ориентации t {p / (p-q)} = {2p / (p-q)}, например t {5/3} = {10/3}.
| Имя | Пентаграмма | Гептаграммы | Октаграмма | Эннеаграммы | Декаграмма | ...н-аграммы | ||
|---|---|---|---|---|---|---|---|---|
| Schläfli | {5/2} | {7/2} | {7/3} | {8/3} т {4/3} | {9/2} | {9/4} | {10/3} т {5/3} | {п / д} |
| Coxeter диаграмма | ||||||||
| Изображение |  |  |  |   |  |  |   | |
Правильные многоугольники, представленные Символ Шлефли {p} для p-угольника. Правильные многоугольники самодвойственны, поэтому выпрямление дает тот же многоугольник. Операция равномерного усечения удваивает стороны до {2p}. Операция snub, чередуя усечение, восстанавливает исходный многоугольник {p}. Таким образом, все однородные многоугольники также правильные. Следующие операции могут быть выполнены с правильными многоугольниками для получения однородных многоугольников, которые также являются правильными многоугольниками:
| Операция | Расширенный Schläfli Символы | Обычный результат | Coxeter диаграмма | Позиция | Симметрия | ||
|---|---|---|---|---|---|---|---|
| (1) | (0) | ||||||
| Родитель | {п} | т0{п} | {п} | {} | -- | [п] (заказ 2p) | |
| Исправленный (Двойной) | г {р} | т1{п} | {п} | -- | {} | [п] (заказ 2p) | |
| Усеченный | т {р} | т0,1{п} | {2p} | {} | {} | [[p]] = [2p] (заказ 4p) | |
| Половина | ч {2p} | {п} | -- | -- | [1+, 2p] = [p] (заказ 2p) | ||
| Курносый | s {p} | {п} | -- | -- | [[п]]+= [p] (заказ 2p) | ||
Три измерения
В трех измерениях ситуация становится интереснее. Есть пять выпуклых правильных многогранников, известных как Платоновы тела:
| Имя | Schläfli {p, q} | Диаграмма | Изображение (прозрачный) | Изображение (твердый) | Изображение (сфера) | Лица {п} | Края | Вершины {q} | Симметрия | Двойной |
|---|---|---|---|---|---|---|---|---|---|---|
| Тетраэдр (3-симплексный) (Пирамида) | {3,3} |  |  |  | 4 {3} | 6 | 4 {3} | Тd | (себя) | |
| Куб (3-куб) (Шестигранник) | {4,3} |  |  |  | 6 {4} | 12 | 8 {3} | Очас | Октаэдр | |
| Октаэдр (3-ортоплекс) | {3,4} |  |  |  | 8 {3} | 12 | 6 {4} | Очас | Куб | |
| Додекаэдр | {5,3} |  |  |  | 12 {5} | 30 | 20 {3}2 | ячас | Икосаэдр | |
| Икосаэдр | {3,5} |  |  |  | 20 {3} | 30 | 12 {5} | ячас | Додекаэдр |
Кроме них существует еще 13 полуправильных многогранников, или Архимедовы тела, который можно получить через Конструкции Wythoff, или выполняя такие операции, как усечение на Платоновых телах, как показано в следующей таблице:
| Родитель | Усеченный | Исправленный | Bitruncated (тр. двойной) | Двунаправленный (двойной) | Собранный | Усеченный (Усеченный) | Курносый | |
|---|---|---|---|---|---|---|---|---|
| Тетраэдр 3-3-2 |  {3,3} |  (3.6.6) |  (3.3.3.3) |  (3.6.6) |  {3,3} |  (3.4.3.4) |  (4.6.6) |  (3.3.3.3.3) |
| Восьмигранный 4-3-2 |  {4,3} |  (3.8.8) |  (3.4.3.4) |  (4.6.6) |  {3,4} |  (3.4.4.4) |  (4.6.8) |  (3.3.3.3.4) |
| Икосаэдр 5-3-2 |  {5,3} |  (3.10.10) |  (3.5.3.5) |  (5.6.6) |  {3,5} |  (3.4.5.4) |  (4.6.10) |  (3.3.3.3.5) |
Также существует бесконечный набор призмы, по одному на каждый правильный многоугольник и соответствующий набор антипризмы.
| # | Имя | Рисунок | Плитка | Вершина фигура | Диаграмма и Schläfli символы |
|---|---|---|---|---|---|
| п2p | Призма |  |  |  | tr {2, p} |
| Ап | Антипризма |  |  |  | sr {2, p} |
Однородные звездные многогранники включают еще 4 правильных звездных многогранника: Многогранники Кеплера-Пуансо, и 53 полуправильных звездных многогранника. Есть также два бесконечных множества: звездные призмы (по одной для каждого звездного многоугольника) и звездные антипризмы (по одной для каждого рационального числа больше 3/2).
Конструкции
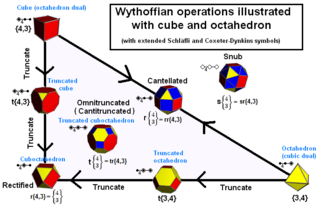
Равномерные многогранники и мозаики Витгоффа могут быть определены их Символ Wythoff, который определяет фундаментальный регион объекта. Расширение Schläfli обозначение, также используемое Coxeter, применяется ко всем размерам; он состоит из буквы 't', за которой следует ряд номеров с индексами, соответствующих окольцованным узлам Диаграмма Кокстера, за которым следует символ Шлефли правильного семенного многогранника. Например, усеченный октаэдр обозначается: t0,1{3,4}.
| Операция | Schläfli Символ | Coxeter диаграмма | Wythoff символ | Позиция: | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Родитель | {p, q} | т0{p, q} | q | 2 шт. | {п} | { } | -- | -- | -- | { } | ||||
| Двунаправленный (или же двойной) | {q, p} | т2{p, q} | p | 2 кв. | -- | { } | {q} | { } | -- | -- | ||||
| Усеченный | т {р, д} | т0,1{p, q} | 2 q | п | {2p} | { } | {q} | -- | { } | { } | ||||
| Bitruncated (или усеченный двойной) | т {д, р} | т1,2{p, q} | 2 п | q | {п} | { } | {2q} | { } | { } | -- | ||||
| Исправленный | г {р, д} | т1{p, q} | 2 | p q | {п} | -- | {q} | -- | { } | -- | ||||
| Собранный (или же расширенный) | рр {р, q} | т0,2{p, q} | p q | 2 | {п} | { }×{ } | {q} | { } | -- | { } | ||||
| Усеченный (или же Усеченный) | tr {p, q} | т0,1,2{p, q} | 2 p q | | {2p} | { }×{} | {2q} | { } | { } | { } | ||||
| Операция | Schläfli Символ | Coxeter диаграмма | Wythoff символ | Позиция: | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Курносый исправленный | sr {p, q} | | 2 р в | {п} | {3} {3} | {q} | -- | -- | -- | |||||
| Курносый | s {p, 2q} | ht0,1{p, q} | с {2p} | {3} | {q} | -- | {3} | ||||||
 |  Создание треугольников |
Четыре измерения
В четырех измерениях есть 6 выпуклые правильные 4-многогранники, 17 призм на Платоновом и Архимедовом телах (исключая куб-призму, которая уже считалась тессеракт) и два бесконечных множества: призмы на выпуклых антипризмах и дуопризма. Также существует 41 выпуклый полуправильный 4-многогранник, включая не уайтоффианец великая антипризма и курносый 24-элементный. Оба этих специальных 4-многогранника составлены из подгрупп вершин многогранника. 600 ячеек.
Не все четырехмерные однородные звездные многогранники перечислены. К ним относятся 10 правильных звездных (Шлефли-Гесса) 4-многогранников и 57 призм на однородных звездных многогранниках, а также три бесконечных семейства: призмы на звездных антипризмах, дуопризмы, образованные умножение два звездных многоугольника и дуопризмы, образованные умножением обычного многоугольника на звездообразный многоугольник. Неизвестное количество 4-многогранников, не подпадающих под указанные выше категории; На данный момент обнаружено более тысячи.

Есть 3 прямых двугранных угла (2 пересекающихся перпендикулярных зеркала):
Ребра с 1 по 2, от 0 до 2 и с 1 по 3.
Каждый правильный многогранник можно рассматривать как образы фундаментальный регион в небольшом количестве зеркал. В 4-мерном многограннике (или 3-мерном кубическом соте) фундаментальная область ограничена четырьмя зеркалами. Зеркало в 4-м пространстве - это трехмерное гиперплоскость, но для наших целей удобнее рассматривать только его двумерное пересечение с трехмерной поверхностью гиперсфера; таким образом, зеркала образуют неправильную форму. тетраэдр.
Каждый из шестнадцати правильные 4-многогранники порождается одной из четырех следующих групп симметрии:
- группа [3,3,3]: 5-элементный {3,3,3}, который самодуален;
- группа [3,3,4]: 16 ячеек {3,3,4} и его двойное тессеракт {4,3,3};
- группа [3,4,3]: 24-элементный {3,4,3}, самодвойственный;
- группа [3,3,5]: 600 ячеек {3,3,5}, его двойное 120 ячеек {5,3,3} и их десять правильных звездочек.
- группа [31,1,1]: содержит только повторяющиеся члены семейства [3,3,4].
(Группы названы в Обозначение Кокстера.)
Восемь из выпуклые однородные соты в евклидовом трехмерном пространстве аналогично порождаются кубические соты {4,3,4}, применяя те же операции, которые использовались для создания однородных 4-многогранников Витоффа.
Для данного симплекса симметрии образующая точка может быть размещена на любой из четырех вершин, 6 ребер, 4 граней или внутреннего объема. На каждом из этих 15 элементов есть точка, изображения которой, отраженные в четырех зеркалах, являются вершинами однородного 4-многогранника.
Расширенные символы Шлефли сделаны т с последующим включением от одного до четырех нижних индексов 0,1,2,3. Если есть один нижний индекс, образующая точка находится в углу основной области, то есть в точке, где встречаются три зеркала. Эти углы обозначены как
- 0: вершина родительского 4-многогранника (центр клетки двойника)
- 1: центр ребра родителя (центр грани дуального)
- 2: центр лица родителя (центр дуального края)
- 3: центр родительской клетки (вершина дуального)
(Для двух самодвойственных 4-многогранников «двойственный» означает аналогичный 4-многогранник в двойном положении.) Два или более нижних индекса означают, что порождающая точка находится между указанными углами.
Конструктивное резюме
Ниже приведены 15 конструктивных форм по семействам. Самодуальные семейства перечислены в одном столбце, а другие - в двух столбцах с общими записями на симметричной Диаграммы Кокстера. В последней 10-й строке перечислены курносые конструкции из 24 ячеек. Сюда входят все непризматические однородные 4-многогранники, кроме не уайтоффианец великая антипризма, у которого нет семьи Кокстеров.
Усеченные формы
В следующей таблице определены все 15 форм. Каждая форма соединительной линии может иметь от одного до четырех типов ячеек, расположенных в позициях 0,1,2,3, как определено выше. Ячейки обозначены многогранным усечением.
- An п-угольная призма представлена как: {n} × {2}.
- Зеленый фон отображается в формах, которые эквивалентны родительской или двойственной.
- Красный фон показывает усечения родителя, а синий - усечения двойника.
| Операция | Символ Шлефли | Coxeter диаграмма | Ячейки по должности: | ||||
|---|---|---|---|---|---|---|---|
| (3) | (2) | (1) | (0) | ||||
| Родитель | {p, q, r} | т0{p, q, r} | {p, q} | -- | -- | -- | |
| Исправленный | г {р, д, г} | т1{p, q, r} | г {р, д} | -- | -- | {q, r} | |
| Двунаправленный (или выпрямленный двойной) | 2r {p, q, r} = г {г, д, р} | т2{p, q, r} | {q, p} | -- | -- | г {д, г} | |
| Триректифицированный (или же двойной) | 3r {p, q, r} = {г, д, р} | т3{p, q, r} | -- | -- | -- | {г, д} | |
| Усеченный | т {р, д, г} | т0,1{p, q, r} | т {р, д} | -- | -- | {q, r} | |
| Bitruncated | 2t {p, q, r} | 2t {p, q, r} | т {д, р} | -- | -- | т {д, г} | |
| Усеченный (или усеченный двойной) | 3t {p, q, r} = t {r, q, p} | т2,3{p, q, r} | {q, p} | -- | -- | т {г, д} | |
| Собранный | rr {p, q, r} | т0,2{p, q, r} | рр {р, q} | -- | {} × {r} | г {д, г} | |
| Двухслойный (или дуальный кантеллированный) | r2r {p, q, r} = rr {r, q, p} | т1,3{p, q, r} | г {р, д} | {p} × {} | -- | rr {q, r} | |
| Runcinated (или же расширенный) | е {р, д, г} | т0,3{p, q, r} | {p, q} | {p} × {} | {} × {r} | {г, д} | |
| Усеченный | tr {p, q, r} | tr {p, q, r} | tr {p, q} | -- | {} × {r} | т {д, г} | |
| Двукратноусеченный (или сокращенное двойное) | t2r {p, q, r} = tr {r, q, p} | т1,2,3{p, q, r} | т {д, р} | {p} × {} | -- | tr {q, r} | |
| Runcitruncated | ет{p, q, r} | т0,1,3{p, q, r} | т {р, д} | {2p} × {} | {} × {r} | rr {q, r} | |
| Runcicantellated (или runcitruncated dual) | е3т{p, q, r} = eт{г, д, р} | т0,2,3{p, q, r} | tr {p, q} | {p} × {} | {} × {2r} | т {г, д} | |
| Runcicantitruncated (или же всесторонне усеченный) | о {п, д, г} | т0,1,2,3{p, q, r} | tr {p, q} | {2p} × {} | {} × {2r} | tr {q, r} | |
Полуформы
Полуконструкции существуют с дыры а не узлы с кольцами. Филиалы соседние дыры а неактивные узлы должны быть чётного порядка. Полуконструкция имеет вершины тождественно окольцованной конструкции.
| Операция | Символ Шлефли | Coxeter диаграмма | Ячейки по должности: | ||||
|---|---|---|---|---|---|---|---|
| (3) | (2) | (1) | (0) | ||||
| Половина Альтернативный | h {p, 2q, r} | ht0{p, 2q, r} | h {p, 2q} | -- | -- | -- | |
| Переменный выпрямленный | ч {2p, 2q, r} | ht1{2p, 2q, r} | ч. {2p, 2q} | -- | -- | ч {2q, r} | |
| Курносый Альтернативное усечение | s {p, 2q, r} | ht0,1{p, 2q, r} | s {p, 2q} | -- | -- | ч {2q, r} | |
| Биснуб Альтернативное усечение битов | 2s {2p, q, 2r} | ht1,2{2p, q, 2r} | s {q, 2p} | -- | -- | s {q, 2r} | |
| Курносый исправленный Переменный усеченный выпрямленный | sr {p, q, 2r} | ht0,1,2{p, q, 2r} | sr {p, q} | -- | с {2,2r} | s {q, 2r} | |
| Омниснуб Альтернативное омнитусечение | os {p, q, r} | ht0,1,2,3{p, q, r} | sr {p, q} | {p} × {} | {} × {r} | sr {q, r} | |
Пять и выше измерений
В пяти и более высоких измерениях существует 3 правильных многогранника: гиперкуб, симплекс и кросс-многогранник. Они являются обобщениями трехмерного куба, тетраэдра и октаэдра соответственно. В этих измерениях нет правильных звездных многогранников. Наиболее однородные многогранники более высокой размерности получаются путем модификации правильных многогранников или путем использования декартова произведения многогранников более низких размерностей.
В шести, семи и восьми измерениях исключительный простые группы Ли, E6, E7 и E8 вступают в игру. Разместив кольца на ненулевом количестве узлов Диаграммы Кокстера, можно получить 63 новых 6-многогранников, 127 новых 7-многогранников и 255 новых 8-многогранников. Ярким примером является 421 многогранник.
Равномерные соты
С темой конечных равномерных многогранников связаны равномерные соты в евклидовом и гиперболическом пространствах. Евклидовы однородные соты образуются аффинные группы Кокстера и гиперболические соты создаются гиперболические группы Кокстера. Две аффинные группы Кокстера можно перемножить.
Есть два класса гиперболических групп Кокстера: компактные и паракомпактные. Равномерные соты, порожденные компактными группами, имеют конечные грани и фигуры вершин и существуют в 2–4 измерениях. Паракомпактные группы имеют аффинные или гиперболические подграфы и бесконечные фасеты или фигуры вершин и существуют в 2-10 измерениях.
Смотрите также
Рекомендации
- Coxeter Красота геометрии: двенадцать эссе, Dover Publications, 1999 г., ISBN 978-0-486-40919-1 (Глава 3: Конструкция Витхоффа для однородных многогранников)
- Норман Джонсон Равномерные многогранники, Рукопись (1991)
- N.W. Джонсон: Теория однородных многогранников и сот, Кандидат наук. Диссертация, Университет Торонто, 1966 г.
- А. Буль Стотт: Геометрическое выведение полуправильных из правильных многогранников и заполнения пространств, Верханделинген академии Конинклийке van Wetenschappen, ширина единицы Амстердам, Eerste Sectie 11,1, Амстердам, 1910 г.
- H.S.M. Coxeter:
- H.S.M. Кокстер, РС. Лонге-Хиггинс и J.C.P. Миллер: Однородные многогранники, Философские труды Лондонского королевского общества, Лондон, 1954 г.
- H.S.M. Кокстер, Правильные многогранники, 3-е издание, Довер, Нью-Йорк, 1973
- Калейдоскопы: Избранные произведения Х.С.М. Coxeter, под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони С. Томпсона, Асии Ивика Вайса, публикации Wiley-Interscience, 1995, ISBN 978-0-471-01003-6
- (Документ 22) Х.С.М. Кокстер, Регулярные и полурегулярные многогранники I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Документ 23) Х.С.М. Кокстер, Правильные и полурегулярные многогранники II, [Math. Zeit. 188 (1985) 559-591]
- (Документ 24) Х.С.М. Кокстер, Правильные и полурегулярные многогранники III, [Math. Zeit. 200 (1988) 3-45]
- Coxeter, Лонге-Хиггинс, Миллер, Равномерные многогранники, Фил. Пер. 1954, 246 А, 401-50. (Использованы расширенные обозначения Шлефли)
- Марко Мёллер, Vierdimensionale Archimedische Polytope, Диссертация, Гамбургский университет, Гамбург (2004) (на немецком)
внешняя ссылка
- Ольшевский, Георгий. «Равномерный многогранник». Глоссарий по гиперпространству. Архивировано из оригинал 4 февраля 2007 г.
- равномерные выпуклые многогранники в четырех измерениях:, Марко Мёллер (на немецком)