WikiDer > Выпрямленный 5-элементный

Rectified 5-cell

Выпрямленный 5-элементный
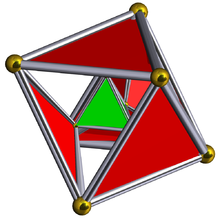Диаграмма Шлегеля с 5 показанными тетраэдрическими ячейками.
Тип	Равномерный 4-многогранник
Символ Шлефли	т₁{3,3,3} или r {3,3,3} {3^2,1} = ${ displaystyle left {{ begin {array} {l} 3 3,3 end {array}} right }}$
Диаграмма Кокстера-Дынкина
Клетки	10	5 {3,3} 5 3.3.3.3
Лица	30 {3}
Края	30
Вершины	10
Фигура вершины	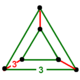Треугольная призма
Группа симметрии	А₄, [3,3,3], порядок 120
Полигон Петри	Пентагон
Характеристики	выпуклый, изогональный, изотоксальный
Единый индекс	1 2 3

В четырехмерный геометрия, то исправленный 5-элементный это равномерный 4-многогранник состоит из 5 правильных тетраэдров и 5 правильных октаэдров клетки. Каждое ребро имеет один тетраэдр и два октаэдра. Каждая вершина состоит из двух тетраэдров и трех октаэдров. Всего у него 30 треугольных граней, 30 ребер и 10 вершин. Каждая вершина окружена 3 октаэдрами и 2 тетраэдрами; то вершина фигуры это треугольная призма.

Топологически, при высшей симметрии [3,3,3], существует только одна геометрическая форма, содержащая 5 правильных тетраэдров и 5 выпрямленных тетраэдров (которая геометрически такая же, как правильный октаэдр). Он также топологически идентичен сегментохорону тетраэдр-октаэдр.^{[требуется разъяснение]}

В вершина фигуры из выпрямленный 5-элементный униформа треугольная призма, образованный тремя октаэдры по бокам и два тетраэдры на противоположных концах.^[1]

Несмотря на то, что имеет такое же количество вершин, что и у ячеек (10), и такое же количество ребер, что и у граней (30), выпрямленная 5-ячейка не является самодвойственной, потому что фигура вершины (однородная треугольная призма) не является двойственной. клетки полихорона.

Строительство Wythoff

Видно в матрица конфигурации, показаны все числа случаев между элементами. Диагональ f-вектор числа выводятся через Строительство Wythoff, разделяя полный порядок групп в порядке подгрупп, удаляя по одному зеркалу за раз.^[2]

А₄	k-лицо	ж_k	ж₀	ж₁	ж₂		ж₃		k-фигура	Примечания
А₂А₁	( )	ж₀	10	6	3	6	3	2	{3} x {}	А₄/ А₂А₁ = 5!/3!/2 = 10
А₁А₁	{ }	ж₁	2	30	1	2	2	1	{} v ()	А₄/ А₁А₁ = 5!/2/2 = 30
А₂А₁	{3}	ж₂	3	3	10	*	2	0	{ }	А₄/ А₂А₁ = 5!/3!/2 = 10
А₂	{3}	ж₂	3	3	*	20	1	1	{ }	А₄/ А₂ = 5!/3! = 20
А₃	г {3,3}	ж₃	6	12	4	4	5	*	( )	А₄/ А₃ = 5!/4! = 5
А₃	{3,3}	ж₃	4	6	0	4	*	5	( )	А₄/ А₃ = 5!/4! = 5

Структура

Вместе с симплексом и 24-элементный, эта форма и ее двойной (многогранник с десятью вершинами и десятью треугольная бипирамида фасеты) был одним из первых известных 2-простых 2-симплициальных 4-многогранников. Это означает, что все его двумерные грани и все двумерные грани двойственного объекта являются треугольниками. В 1997 году Том Брэйден нашел еще одну двойную пару примеров, склеив вместе два выпрямленных 5-элементных элемента; с тех пор было построено бесконечно много 2-простых 2-симплициальных многогранников.^[3]^[4]

Полуправильный многогранник

Это один из трех полурегулярный 4-многогранник состоит из двух или более ячеек, которые Платоновы тела, обнаруженный Торольд Госсет в его статье 1900 года. Он назвал это тетроктаэдрический для того, чтобы быть сделанным из тетраэдр и октаэдр клетки.^[5]

Э. Л. Элте идентифицировал его в 1912 году как полуправильный многогранник, обозначив его как tC₅.

Альтернативные имена

Тетроктаэдрический (Торольд Госсет)
Диспентахорон
Выпрямленный 5-элементный (Норман В. Джонсон)
Исправленный 4-симплексный
Полностью усеченный 4-симплексный
Ректифицированный пентахорон (Акроним: рэп) (Джонатан Бауэрс)
Амбопентахорон (Нил Слоан и Джон Хортон Конвей)
(5,2)-гиперсимплекс (выпуклая оболочка пятимерных (0,1) -векторов ровно с двумя)

Изображений

орфографические проекции
А_k Самолет Кокстера	А₄	А₃	А₂
График
Двугранная симметрия	[5]	[4]	[3]

стереографическая проекция (сосредоточено на октаэдр)	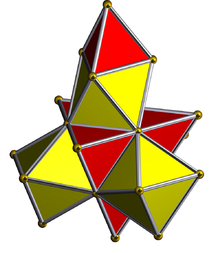Сеть (многогранник)
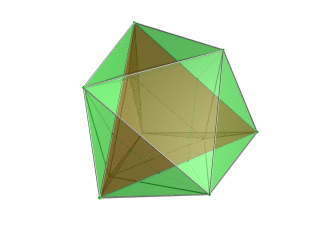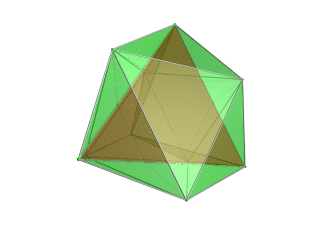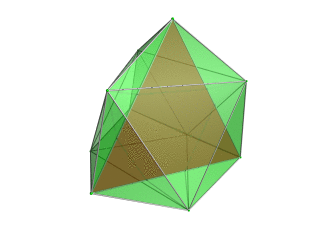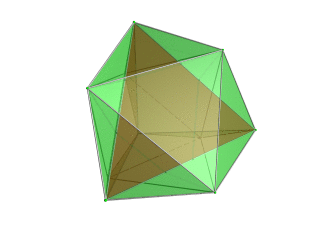	Тетраэдр-центрированная перспективная проекция в трехмерное пространство, при этом ближайший к четырехмерной точке обзора тетраэдр отображается красным цветом, а 4 окружающих октаэдра - зеленым. Ячейки, лежащие на дальней стороне многогранника, отбракованы для наглядности (хотя их можно различить по контурам ребер). Поворот выполняется только для трехмерного проекционного изображения, чтобы показать его структуру, а не для поворота в четырехмерном пространстве.

Координаты

В Декартовы координаты вершин выпрямленной 5-ячейки с центром в начале координат и длиной ребра 2 составляют:

Координаты
${ displaystyle left ({ sqrt { frac {2} {5}}}, { frac {2} { sqrt {6}}}, { frac {2} { sqrt {3}) }}, 0 right)}$ ${ displaystyle left ({ sqrt { frac {2} {5}}}, { frac {2} { sqrt {6}}}, { frac {-1} { sqrt {3) }}}, pm 1 right)}$ ${ displaystyle left ({ sqrt { frac {2} {5}}}, { frac {-2} { sqrt {6}}}, { frac {1} { sqrt {3) }}}, pm 1 right)}$ ${ displaystyle left ({ sqrt { frac {2} {5}}}, { frac {-2} { sqrt {6}}}, { frac {-2} { sqrt { 3}}}, 0 right)}$	${ displaystyle left ({ frac {-3} { sqrt {10}}}, { frac {1} { sqrt {6}}}, { frac {1} { sqrt {3) }}}, pm 1 right)}$ ${ displaystyle left ({ frac {-3} { sqrt {10}}}, { frac {1} { sqrt {6}}}, { frac {-2} { sqrt { 3}}}, 0 right)}$ ${ displaystyle left ({ frac {-3} { sqrt {10}}}, - { sqrt { frac {3} {2}}}, 0, 0 right)}$

Проще говоря, вершины выпрямленный 5-элементный можно разместить на гиперплоскость в 5-мерном пространстве как перестановки (0,0,0,1,1) или же (0,0,1,1,1). Эти конструкции можно рассматривать как положительные ортодоксальный грани выпрямленный пентакросс или же двунаправленный пентеракт соответственно.

Связанные многогранники

Выпуклая оболочка выпрямленной 5-ячейки и двойственной ей (в предположении, что они конгруэнтны) представляют собой неоднородный полихорон, состоящий из 30 ячеек: 10 тетраэдры, 20 октаэдры (как треугольные антипризмы) и 20 вершин. Его фигура вершины - треугольный двустворчатый.

Связанные 4-многогранники

Этот многогранник является вершина фигуры из 5-полукруглый, а край фигуры униформы 2₂₁ многогранник.

Это также один из 9 Равномерные 4-многогранники построенный из [3,3,3] Группа Коксетера.

Имя	5-элементный	усеченный 5-элементный	выпрямленный 5-элементный	скошенный 5-элементный	усеченный по битам 5-элементный	усеченный 5-элементный	5-клеточный	усеченный 5-элементный	омниусеченный 5-элементный
Schläfli символ	{3,3,3} 3r {3,3,3}	т {3,3,3} 2т {3,3,3}	г {3,3,3} 2r {3,3,3}	рр {3,3,3} r2r {3,3,3}	2т {3,3,3}	tr {3,3,3} t2r {3,3,3}	т_0,3{3,3,3}	т_0,1,3{3,3,3} т_0,2,3{3,3,3}	т_0,1,2,3{3,3,3}
Coxeter диаграмма
Шлегель диаграмма
А₄ Самолет Кокстера График
А₃ Самолет Кокстера График
А₂ Самолет Кокстера График

Связанные многогранники и соты

Выпрямленный 5-элементный является вторым в размерной серии полуправильные многогранники. Каждый прогрессивный равномерный многогранник построен как вершина фигуры предыдущего многогранника. Торольд Госсет идентифицировал эту серию в 1900 году как содержащую все правильный многогранник грани, содержащие все симплексы и ортоплексы (тетраэдры и октаэдры в случае выпрямленного 5-ти элементного). В Символ Кокстера для выпрямленного 5-элементного 0₂₁.

k₂₁ цифры в n мерном
Космос	Конечный						Евклидово	Гиперболический
E_п	3	4	5	6	7	8	9	10
Coxeter группа	E₃= А₂А₁	E₄= А₄	E₅= D₅	E₆	E₇	E₈	E₉ = ${ displaystyle { tilde {E}} _ {8}}$ = E₈⁺	E₁₀ = ${ displaystyle { bar {T}} _ {8}}$ = E₈⁺⁺
Coxeter диаграмма
Симметрия	[3^−1,2,1]	[3^0,2,1]	[3^1,2,1]	[3^2,2,1]	[3^3,2,1]	[3^4,2,1]	[3^5,2,1]	[3^6,2,1]
Заказ	12	120	1,920	51,840	2,903,040	696,729,600	∞
График							-	-
Имя	−1₂₁	0₂₁	1₂₁	2₂₁	3₂₁	4₂₁	5₂₁	6₂₁

Изотопные многогранники

Изотопные однородные усеченные симплексы
Дим.	2	3	4	5	6	7	8
Имя Coxeter	Шестиугольник = t {3} = {6}	Октаэдр = г {3,3} = {3^1,1} = {3,4} ${ displaystyle left {{ begin {array} {l} 3 3 end {array}} right }}$	Декахорон 2т {3³}	Додекатерон 2r {3⁴} = {3^2,2} ${ displaystyle left {{ begin {array} {l} 3,3 3,3 end {array}} right }}$	Тетрадекапетон 3т {3⁵}	Гексадекаэксон 3r {3⁶} = {3^3,3} ${ displaystyle left {{ begin {array} {l} 3,3,3 3,3,3 end {array}} right }}$	Octadecazetton 4т {3⁷}
Изображений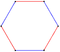
Фигура вершины	() v ()	{ }×{ }	{} v {}	{3}×{3}	{3} v {3}	{3,3} x {3,3}	{3,3} v {3,3}
Грани		{3}	т {3,3}	г {3,3,3}	2т {3,3,3,3}	2r {3,3,3,3,3}	3т {3,3,3,3,3,3}
В качестве пересекающийся двойной симплексы	∩	∩	∩	∩	∩	∩	∩

Смотрите также

Полуправильный многогранник k 21

Примечания

^ Конвей, 2008
^ Клитцинг, Ричард. "o3x4o3o - рэп".
^ Эппштейн, Дэвид; Куперберг, Грег; Циглер, Гюнтер М. (2003), «Толстые 4-многогранники и более толстые 3-сферы», Бездек, Андраш (ред.), Дискретная геометрия: К 60-летию В. Куперберга., Чистая и прикладная математика, 253, стр. 239–265, arXiv:math.CO/0204007.
^ Паффенхольц, Андреас; Циглер, Гюнтер М. (2004), "The E_т-конструкция решеток, сфер и многогранников », Дискретная и вычислительная геометрия, 32 (4): 601–621, arXiv:math.MG/0304492, Дои:10.1007 / s00454-004-1140-4, МИСТЕР 2096750, S2CID 7603863.
^ Госсет, 1900 г.

внешняя ссылка

Выпрямленный 5-элементный - данные и изображения
- 1. Выпуклая однородная полихора на основе пентахороны - Модель 2., Георгий Ольшевский.
Клитцинг, Ричард. "4D однородные многогранники (полихоры) x3o3o3o - rap".

v т е Фундаментальный выпуклый обычный и однородные многогранники в размерах 2–10
Семья	А_п	B_п	я₂(п) / D_п	E₆ / E₇ / E₈ / F₄ / грамм₂	ЧАС_п
Правильный многоугольник	Треугольник	Квадрат	п-угольник	Шестиугольник	Пентагон
Равномерный многогранник	Тетраэдр	Октаэдр • Куб	Демикуб		Додекаэдр • Икосаэдр
Равномерный 4-многогранник	5-элементный	16 ячеек • Тессеракт	Demitesseract	24-элементный	120 ячеек • 600 ячеек
Равномерный 5-многогранник	5-симплекс	5-ортоплекс • 5-куб	5-полукруглый
Равномерный 6-многогранник	6-симплекс	6-ортоплекс • 6-куб	6-полукуб	1₂₂ • 2₂₁
Равномерный 7-многогранник	7-симплекс	7-ортоплекс • 7-куб	7-полукруглый	1₃₂ • 2₃₁ • 3₂₁
Равномерный 8-многогранник	8-симплекс	8-ортоплекс • 8-куб	8-полукруглый	1₄₂ • 2₄₁ • 4₂₁
Равномерный 9-многогранник	9-симплекс	9-ортоплекс • 9-куб	9-полукруглый
Равномерный 10-многогранник	10-симплекс	10-ортоплекс • 10-куб	10-полукуб
Униформа п-многогранник	п-симплекс	п-ортоплекс • п-куб	п-полукуб	1_k2 • 2_k1 • k₂₁	п-пятиугольный многогранник
Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений

[1] Конвей, 2008

[2] Клитцинг, Ричард. "o3x4o3o - рэп".

[3] Эппштейн, Дэвид; Куперберг, Грег; Циглер, Гюнтер М. (2003), «Толстые 4-многогранники и более толстые 3-сферы», Бездек, Андраш (ред.), Дискретная геометрия: К 60-летию В. Куперберга., Чистая и прикладная математика, 253, стр. 239–265, arXiv:math.CO/0204007.

[4] Паффенхольц, Андреас; Циглер, Гюнтер М. (2004), "The E_т-конструкция решеток, сфер и многогранников », Дискретная и вычислительная геометрия, 32 (4): 601–621, arXiv:math.MG/0304492, Дои:10.1007 / s00454-004-1140-4, МИСТЕР 2096750, S2CID 7603863.

[5] Госсет, 1900 г.

[1]

[2]

[3]

[4]

[5]

Navigation