WikiDer > Собранный 5-элементный

Cantellated 5-cell

Ортогональные проекции в₄ Самолет Кокстера
5-элементный	Собранный 5-элементный	Cantitruncated 5-элементный

В четырехмерном геометрия, а скошенный 5-элементный выпуклый равномерный 4-многогранник, быть песня (усечение 2-го порядка, до строгание кромок) регулярного 5-элементный.

Есть 2 уникальные степени выполнения 5-ячеек, включая усечения перестановок.

Собранный 5-элементный

Собранный 5-элементный
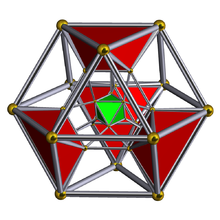Диаграмма Шлегеля с показаны октаэдрические ячейки
Тип	Равномерный 4-многогранник
Символ Шлефли	т_0,2{3,3,3} рр {3,3,3}
Диаграмма Кокстера
Клетки	20	5 (3.4.3.4) 5 (3.3.3.3) 10 (3.4.4)
Лица	80	50{3} 30{4}
Края	90
Вершины	30
Фигура вершины	Квадратный клин
Группа симметрии	А₄, [3,3,3], порядок 120
Характеристики	выпуклый, изогональный
Единый индекс	3 4 5

Сеть

В скошенный 5-элементный или же малый ромбовидный пентахорон это равномерный 4-многогранник. У него 30 вершин, 90 ребер, 80 граней и 20 ячеек. Ячейки 5 кубооктаэдр, 5 октаэдры, и 10 треугольные призмы. Каждая вершина окружена двумя кубооктаэдрами, двумя треугольными призмами и одним октаэдром; то вершина фигуры - неоднородная треугольная призма.

Альтернативные имена

Кантеллированный пентахорон
Собранный 4-симплексный
(малый) призматодиспентахорон
Ректифицированный диспентахорон
Маленький ромбовидный пентахорон (Сокращение: Srip) (Джонатан Бауэрс)

Изображений

орфографические проекции
А_k Самолет Кокстера	А₄	А₃	А₂
График
Двугранная симметрия	[5]	[4]	[3]

Каркас	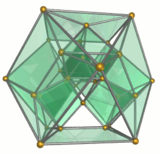Десять треугольные призмы окрашен в зеленый цвет	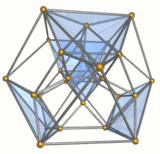Пять октаэдры окрашен в синий цвет

Координаты

В Декартовы координаты вершин скошенной 5-ячейки с центром в начале координат и длиной ребра 2 составляют:

Координаты
${displaystyle left (2 {sqrt {frac {2} {5}}}, 2 {sqrt {frac {2} {3}}}, {frac {1} {sqrt {3}}}, pm 1ight)}$ ${displaystyle left (2 {sqrt {frac {2} {5}}}, 2 {sqrt {frac {2} {3}}}, {frac {-2} {sqrt {3}}}, 0ight)}$ ${displaystyle left (2 {sqrt {frac {2} {5}}}, 0, pm {sqrt {3}}, pm 1ight)}$ ${displaystyle left (2 {sqrt {frac {2} {5}}}, 0, 0, pm 2ight)}$ ${displaystyle left (2 {sqrt {frac {2} {5}}}, -2 {sqrt {frac {2} {3}}}, {frac {2} {sqrt {3}}}, 0ight)}$ ${displaystyle left (2 {sqrt {frac {2} {5}}}, -2 {sqrt {frac {2} {3}}}, {frac {-1} {sqrt {3}}}, pm 1ight) }$ ${displaystyle left ({frac {-1} {sqrt {10}}}, {sqrt {frac {3} {2}}}, pm {sqrt {3}}, pm 1ight)}$	${displaystyle left ({frac {-1} {sqrt {10}}}, {sqrt {frac {3} {2}}}, 0, pm 2ight)}$ ${displaystyle left ({frac {-1} {sqrt {10}}}, {frac {-1} {sqrt {6}}}, {frac {2} {sqrt {3}}}, pm 2ight)}$ ${displaystyle left ({frac {-1} {sqrt {10}}}, {frac {-1} {sqrt {6}}}, {frac {-4} {sqrt {3}}}, 0ight)}$ ${displaystyle left ({frac {-1} {sqrt {10}}}, {frac {-5} {sqrt {6}}}, {frac {1} {sqrt {3}}}, pm 1ight)}$ ${displaystyle left ({frac {-1} {sqrt {10}}}, {frac {-5} {sqrt {6}}}, {frac {-2} {sqrt {3}}}, 0ight)}$ ${displaystyle left (-3 {sqrt {frac {2} {5}}}, 0, 0, 0ight) pm left (0, {sqrt {frac {2} {3}}}, {frac {2} {sqrt {3}}}, 0ight)}$ ${displaystyle left (-3 {sqrt {frac {2} {5}}}, 0, 0, 0ight) pm left (0, {sqrt {frac {2} {3}}}, {frac {-1} { sqrt {3}}}, pm 1ight)}$

Вершины скошенный 5-элементный проще всего разместить в 5-м пространстве как перестановки:

(0,0,1,1,2)

Эта конструкция взята из положительного ортодоксальный грань скошенный 5-ортоплекс.

Связанные многогранники

Выпуклая оболочка двух скошенных 5-ячеек в противоположных положениях представляет собой неоднородный полихорон, состоящий из 100 ячеек: трех видов по 70 октаэдры (10 выпрямленных тетраэдров, 20 треугольных антипризм, 40 треугольных антиподий), 30 тетраэдры (как тетрагональные дифеноиды) и 60 вершин. Его вершина - это фигура, топологически эквивалентная куб с треугольная призма прикреплен к одной из его квадратных граней.

Фигура вершины

Cantitruncated 5-элементный

Cantitruncated 5-элементный
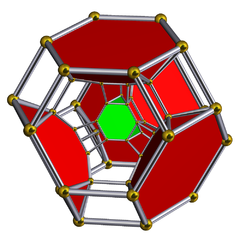Диаграмма Шлегеля показаны усеченные тетраэдрические ячейки
Тип	Равномерный 4-многогранник
Символ Шлефли	т_0,1,2{3,3,3} tr {3,3,3}
Диаграмма Кокстера
Клетки	20	5 (4.6.6) 10 (3.4.4) 5 (3.6.6)
Лица	80	20{3} 30{4} 30{6}
Края	120
Вершины	60
Фигура вершины	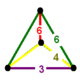клиновидная
Группа симметрии	А₄, [3,3,3], порядок 120
Характеристики	выпуклый, изогональный
Единый индекс	6 7 8

Сеть

В усеченный 5-элементный или же большой ромбовидный пентахорон это равномерный 4-многогранник. Он состоит из 60 вершин, 120 ребер, 80 граней и 20 ячеек. Ячейки: 5 усеченные октаэдры, 10 треугольные призмы, и 5 усеченные тетраэдры. Каждая вершина окружена двумя усеченными октаэдрами, одной треугольной призмой и одним усеченным тетраэдром.

Альтернативные названия

Гантусеченный пентахорон
Усеченный 4-симплексный
Большой призматодиспентахорон
Усеченный диспентахорон
Большой ромбовидный пентахорон (Акроним: хватка) (Джонатан Бауэрс)

Изображений

орфографические проекции
А_k Самолет Кокстера	А₄	А₃	А₂
График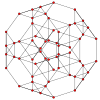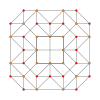
Двугранная симметрия	[5]	[4]	[3]

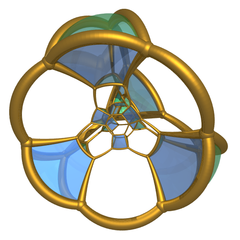Стереографическая проекция с его 10 треугольные призмы.

Декартовы координаты

В Декартовы координаты усеченных 5-ячеек с центром в исходной точке и длиной ребра 2:

Координаты
${displaystyle left (3 {sqrt {frac {2} {5}}}, pm {sqrt {6}}, pm {sqrt {3}}, pm 1ight)}$ ${displaystyle left (3 {sqrt {frac {2} {5}}}, pm {sqrt {6}}, 0, pm 2ight)}$ ${displaystyle left (3 {sqrt {frac {2} {5}}}, 0, 0, 0ight) pm left (0, {sqrt {frac {2} {3}}}, {frac {5} {sqrt { 3}}}, 13 вечера)}$ ${displaystyle left (3 {sqrt {frac {2} {5}}}, 0, 0, 0ight) pm left (0, {sqrt {frac {2} {3}}}, {frac {-1} {sqrt) {3}}}, 3 вечера)}$ ${displaystyle left (3 {sqrt {frac {2} {5}}}, 0, 0, 0ight) pm left (0, {sqrt {frac {2} {3}}}, {frac {-4} {sqrt) {3}}}, 2 вечера)}$ ${displaystyle left ({frac {1} {sqrt {10}}}, {frac {5} {sqrt {6}}}, {frac {5} {sqrt {3}}}, pm 1ight)}$ ${displaystyle left ({frac {1} {sqrt {10}}}, {frac {5} {sqrt {6}}}, {frac {-1} {sqrt {3}}}, pm 3ight)}$ ${displaystyle left ({frac {1} {sqrt {10}}}, {frac {5} {sqrt {6}}}, {frac {-4} {sqrt {3}}}, pm 2ight)}$ ${displaystyle left ({frac {1} {sqrt {10}}}, - {sqrt {frac {3} {2}}}, {sqrt {3}}, pm 3ight)}$ ${displaystyle left ({frac {1} {sqrt {10}}}, - {sqrt {frac {3} {2}}}, -2 {sqrt {3}}, 0ight)}$ ${displaystyle left ({frac {1} {sqrt {10}}}, {frac {-7} {sqrt {6}}}, {frac {2} {sqrt {3}}}, pm 2ight)}$ ${displaystyle left ({frac {1} {sqrt {10}}}, {frac {-7} {sqrt {6}}}, {frac {-4} {sqrt {3}}}, 0ight)}$ ${displaystyle left (-2 {sqrt {frac {2} {5}}}, 2 {sqrt {frac {2} {3}}}, {frac {4} {sqrt {3}}}, pm 2ight)}$	${displaystyle left (-2 {sqrt {frac {2} {5}}}, 2 {sqrt {frac {2} {3}}}, {frac {1} {sqrt {3}}}, pm 3ight)}$ ${displaystyle left (-2 {sqrt {frac {2} {5}}}, 2 {sqrt {frac {2} {3}}}, {frac {-5} {sqrt {3}}}, pm 1ight) }$ ${displaystyle left (-2 {sqrt {frac {2} {5}}}, 0, {sqrt {3}}, pm 3ight)}$ ${displaystyle left (-2 {sqrt {frac {2} {5}}}, 0, -2 {sqrt {3}}, 0ight)}$ ${displaystyle left (-2 {sqrt {frac {2} {5}}}, -4 {sqrt {frac {2} {3}}}, {frac {1} {sqrt {3}}}, pm 1ight) }$ ${displaystyle left (-2 {sqrt {frac {2} {5}}}, -4 {sqrt {frac {2} {3}}}, {frac {-2} {sqrt {3}}}, 0ight) }$ ${displaystyle left ({frac {-9} {sqrt {10}}}, {sqrt {frac {3} {2}}}, pm {sqrt {3}}, pm 1ight)}$ ${displaystyle left ({frac {-9} {sqrt {10}}}, {sqrt {frac {3} {2}}}, 0, pm 2ight)}$ ${displaystyle left ({frac {-9} {sqrt {10}}}, {frac {-1} {sqrt {6}}}, {frac {2} {sqrt {3}}}, pm 2ight)}$ ${displaystyle left ({frac {-9} {sqrt {10}}}, {frac {-1} {sqrt {6}}}, {frac {-4} {sqrt {3}}}, 0ight)}$ ${displaystyle left ({frac {-9} {sqrt {10}}}, {frac {-5} {sqrt {6}}}, {frac {1} {sqrt {3}}}, pm 1ight)}$ ${displaystyle left ({frac {-9} {sqrt {10}}}, {frac {-5} {sqrt {6}}}, {frac {-2} {sqrt {3}}}, 0ight)}$

Эти вершины проще построить на гиперплоскость в 5-м пространстве, как перестановки из:

(0,0,1,2,3)

Эта конструкция взята из положительного ортодоксальный грань из усеченный 5-ортоплекс.

Связанные многогранники

Конструкция двойной симметрии может быть получена путем размещения усеченных тетраэдров на усеченных октаэдрах, в результате чего получается неоднородный полихорон с 10 усеченные тетраэдры, 20 шестиугольные призмы (как дитригональные трапеции), два вида 80 треугольные призмы (20 с D_3ч симметрия и 60 C_2v-симметричные клинья) и 30 тетраэдры (как тетрагональные дифеноиды). Его вершинная фигура топологически эквивалентна октаэдр.

Фигура вершины

Связанные 4-многогранники

Эти многогранники представляют собой набор из 9 Равномерные 4-многогранники построенный из [3,3,3] Группа Коксетера.

Имя	5-элементный	усеченный 5-элементный	выпрямленный 5-элементный	скошенный 5-элементный	усеченный по битам 5-элементный	усеченный 5-элементный	5-клеточный	усеченный 5-элементный	омниусеченный 5-элементный
Schläfli символ	{3,3,3} 3r {3,3,3}	т {3,3,3} 2т {3,3,3}	г {3,3,3} 2r {3,3,3}	рр {3,3,3} r2r {3,3,3}	2т {3,3,3}	tr {3,3,3} t2r {3,3,3}	т_0,3{3,3,3}	т_0,1,3{3,3,3} т_0,2,3{3,3,3}	т_0,1,2,3{3,3,3}
Coxeter диаграмма
Шлегель диаграмма
А₄ Самолет Кокстера График
А₃ Самолет Кокстера График
А₂ Самолет Кокстера График

Рекомендации

H.S.M. Coxeter:
- H.S.M. Кокстер, Правильные многогранники, 3-е издание, Довер, Нью-Йорк, 1973
- Калейдоскопы: Избранные произведения Х.С.М. Coxeter, под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони С. Томпсона, Асии Ивика Вайса, публикации Wiley-Interscience, 1995, ISBN 978-0-471-01003-6 [1]
  - (Документ 22) Х.С.М. Кокстер, Регулярные и полурегулярные многогранники I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
  - (Документ 23) Х.С.М. Кокстер, Правильные и полурегулярные многогранники II, [Math. Zeit. 188 (1985) 559-591]
  - (Документ 24) Х.С.М. Кокстер, Правильные и полурегулярные многогранники III, [Math. Zeit. 200 (1988) 3-45]
Норман Джонсон Равномерные многогранники, Рукопись (1991)
- N.W. Джонсон: Теория однородных многогранников и сот, Кандидат наук. (1966)
1. Выпуклая однородная полихора на основе пентахорон - Модель 4, 7., Георгий Ольшевский.
Клитцинг, Ричард. «4D однородные многогранники (полихоры)». x3o3x3o - рукоятка, x3x3x3o - рукоятка

v т е Фундаментальный выпуклый обычный и однородные многогранники в размерах 2–10
Семья	А_п	B_п	я₂(п) / D_п	E₆ / E₇ / E₈ / F₄ / грамм₂	ЧАС_п
Правильный многоугольник	Треугольник	Квадрат	п-угольник	Шестиугольник	Пентагон
Равномерный многогранник	Тетраэдр	Октаэдр • Куб	Демикуб		Додекаэдр • Икосаэдр
Равномерный 4-многогранник	5-элементный	16 ячеек • Тессеракт	Demitesseract	24-элементный	120 ячеек • 600 ячеек
Равномерный 5-многогранник	5-симплекс	5-ортоплекс • 5-куб	5-полукуб
Равномерный 6-многогранник	6-симплекс	6-ортоплекс • 6-куб	6-полукуб	1₂₂ • 2₂₁
Равномерный 7-многогранник	7-симплекс	7-ортоплекс • 7-куб	7-полукуб	1₃₂ • 2₃₁ • 3₂₁
Равномерный 8-многогранник	8-симплекс	8-ортоплекс • 8-куб	8-полукруглый	1₄₂ • 2₄₁ • 4₂₁
Равномерный 9-многогранник	9-симплекс	9-ортоплекс • 9-куб	9-полукуб
Равномерный 10-многогранник	10-симплекс	10-ортоплекс • 10-куб	10-полукуб
Униформа п-многогранник	п-симплекс	п-ортоплекс • п-куб	п-полукуб	1_k2 • 2_k1 • k₂₁	п-пятиугольный многогранник
Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений

Navigation

Navigation

Themenportale

WikiDer > Собранный 5-элементный

Содержание

Собранный 5-элементный

Альтернативные имена

Изображений

Координаты

Связанные многогранники

Cantitruncated 5-элементный

Альтернативные названия

Изображений

Декартовы координаты

Связанные многогранники

Связанные 4-многогранники

Рекомендации