WikiDer > Runcination
Эта статья включает Список ссылок, связанное чтение или внешняя ссылка, но его источники остаются неясными, потому что в нем отсутствует встроенные цитаты. (Март 2015 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
В геометрия, бегство это операция, которая разрезает правильный многогранник (или же соты) одновременно вдоль граней, ребер и вершин, создавая новые фасеты вместо исходных центров граней, ребер и вершин.[нужна цитата]
Это операция усечения более высокого порядка, следующая за песня, и усечение.
Он представлен расширенным Символ Шлефли т0,3{p, q, ...}. Эта операция существует только для 4-многогранники {p, q, r} или выше.
Эта операция двойственно симметрична для регулярных равномерные 4-многогранники и 3-х местный выпуклые однородные соты.
Для правильного 4-многогранника {p, q, r} исходные клетки {p, q} остаются, но становятся разделенными. Зазоры на разделенных гранях становятся п-угольные призмы. Зазоры между разделенными краями становятся р-угольные призмы. Промежутки между разделенными вершинами становятся {r, q} ячейками. В вершина фигуры для правильного 4-многогранника {p, q, r} является q-гональный антипризма (называется антиподиум если п и р разные).
Для правильных 4-многогранников / сот эта операция также называется расширение к Алисия Буль Стотт, как это представляется путем перемещения ячеек регулярной формы от центра и заполнения новых граней в промежутках для каждой открытой вершины и ребра.
Бегунковые 4-многогранники / сотовые формы:
| Символ Шлефли Диаграмма Кокстера | Имя | Фигура вершины | Изображение |
|---|---|---|---|
| Равномерные 4-многогранники | |||
| т0,3{3,3,3} | Ранцинированный 5-клеточный |  |  |
| т0,3{3,3,4} | Ранцинированный 16-ти клеточный (Такой же как беглый 8-клеточный) |  |   |
| т0,3{3,4,3} | Ранцинированный 24-элементный |  |  |
| т0,3{3,3,5} | Ранцинированный 120-клеточный (Такой же как беглый 600-клеточный) |  |  |
| Евклидово выпуклые однородные соты | |||
| т0,3{4,3,4} | Плетеные кубические соты (Такой же как кубические соты) | 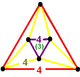 |  |
| Гиперболический однородные соты | |||
| т0,3{4,3,5} | Сотовидный соты порядка 5 куб. |  | |
| т0,3{3,5,3} | Ячеистые икосаэдрические соты | 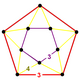 | |
| т0,3{5,3,5} | Додекаэдрические соты Runcinated порядка 5 |  | |
Смотрите также
- Равномерный многогранник
- Равномерный 4-многогранник
- Ректификация (геометрия)
- Усечение (геометрия)
- Cantellation (геометрия)
Рекомендации
- Кокстер, H.S.M. Правильные многогранники, (3-е издание, 1973 г.), Дуврское издание, ISBN 0-486-61480-8 (стр. 145–154 Глава 8: Усечение, стр. 210 Расширение)
- Норман Джонсон Равномерные многогранники, Рукопись (1991)
- N.W. Джонсон: Теория однородных многогранников и сот, Кандидат наук. Диссертация, Университет Торонто, 1966 г.
- Джон Х. Конвей, Хайди Берджель, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 26)
