WikiDer > Полуикосаэдр
| Полуикосаэдр | |
|---|---|
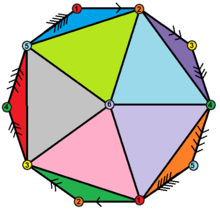 десятиугольный Диаграмма Шлегеля | |
| Тип | абстрактный правильный многогранник глобально проективный многогранник |
| Лица | 10 треугольники |
| Края | 15 |
| Вершины | 6 |
| Конфигурация вершины | 3.3.3.3.3 |
| Символ Шлефли | {3,5} / 2 или {3,5}5 |
| Группа симметрии | А5, заказ 60 |
| Двойной многогранник | полудодекаэдр |
| Свойства | неориентируемый Эйлерова характеристика 1 |
А полуикосаэдр является абстрактный правильный многогранник, содержащую половину граней правильный икосаэдр. Это может быть реализовано как проективный многогранник (а мозаика из реальная проективная плоскость 10 треугольниками), что можно визуализировать, построив проективную плоскость в виде полушарие где противоположные точки вдоль границы соединяются и разделяют полушарие на три равные части.
Геометрия
У него 10 треугольных граней, 15 ребер и 6 вершин.
Это также связано с невыпуклым равномерный многогранник, то тетрагемигексаэдр, который может быть топологически идентичен полуикосаэдру, если каждую из трех квадратных граней разделить на два треугольника.
Графики
Его можно симметрично представить на гранях, а вершины в виде диаграммы Шлегеля:
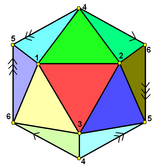 |
| По центру лица |
|---|
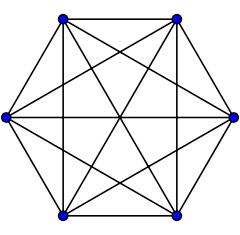
Полный граф K6
Он имеет те же вершины и ребра, что и 5-мерный 5-симплекс который имеет полный граф ребер, но содержит только половину (20) граней.
С точки зрения теория графов это вложение (в полный график с 6 вершинами) на реальная проективная плоскость. Благодаря этому встраиванию двойственный граф это Граф Петерсена --- увидеть полудодекаэдр.
Смотрите также
- 11-элементный - абстрактное регулярное 4-многогранник построена из 11 полуикосаэдров.
- полудодекаэдр
- полукуб
- полуоктаэдр
использованная литература
- Макмаллен, Питер; Шульте, Эгон (декабрь 2002 г.), "6C. Проективные регулярные многогранники", Абстрактные правильные многогранники (1-е изд.), Cambridge University Press, стр.162–165, ISBN 0-521-81496-0
