WikiDer > Неравенство средних арифметических и геометрических

Доказательство без слов из неравенство средних арифметических и геометрических:
PR - диаметр круга с центром в точке O; его радиус AO равен среднее арифметическое из а и б. С использованием теорема о среднем геометрическом, треугольник PGR высота GQ - это среднее геометрическое. Для любого соотношения а:б, АО ≥ GQ.

Визуальное доказательство который (Икс + у)² ≥ 4ху. Извлечение квадратного корня и деление на два дает неравенство AM – GM.^[1]

В математика, то неравенство средних арифметических и геометрических, или короче AM – GM неравенство, заявляет, что среднее арифметическое списка неотрицательных действительные числа больше или равно среднее геометрическое того же списка; и далее, что два средних значения равны если и только если все числа в списке одинаковые.

Простейший нетривиальный случай - то есть с более чем одной переменной - для двух неотрицательных чисел Икс иу, это утверждение, что

${ displaystyle { frac {x + y} {2}} geq { sqrt {xy}}}$

с равенством тогда и только тогда, когда Икс = у. Этот случай можно увидеть из того факта, что квадрат действительного числа всегда неотрицателен (больше или равен нулю), и из элементарного случая (а ± б)² = а² ± 2ab + б² из биномиальная формула:

${ displaystyle { begin {align} 0 & leq (xy) ^ {2} & = x ^ {2} -2xy + y ^ {2} & = x ^ {2} + 2xy + y ^ {2} -4xy & = (x + y) ^ {2} -4xy. End {align}}}$

Следовательно (Икс + у)² ≥ 4ху, с равенством именно тогда, когда (Икс − у)² = 0, т.е. Икс = у. Тогда неравенство AM – GM следует из извлечения положительного квадратного корня из обеих частей и последующего деления обеих частей на 2.

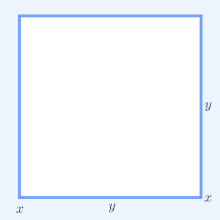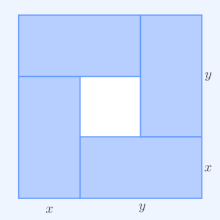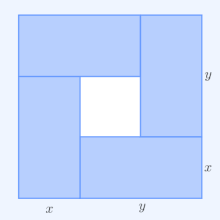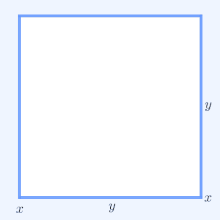
Для геометрической интерпретации рассмотрим прямоугольник со сторонами длиныИкс иу, следовательно, он имеет периметр 2Икс + 2у и площадь ху. Аналогично квадрат со всех сторон длины √ху имеет периметр 4√ху и той же площади, что и прямоугольник. В простейшем нетривиальном случае неравенства AM – GM для периметров следует, что 2Икс + 2у ≥ 4√ху и что только квадрат имеет наименьший периметр среди всех прямоугольников равной площади.

Доступны расширения неравенства AM – GM, включая веса или же обобщенные средства.

Фон

В среднее арифметическое, или менее точно средний, из списка п числа Икс₁, Икс₂, . . . , Икс_п это сумма чисел, деленная нап:

${ displaystyle { frac {x_ {1} + x_ {2} + cdots + x_ {n}} {n}}.}$

В среднее геометрическое аналогичен, за исключением того, что он определен только для списка неотрицательный действительные числа, и использует умножение и корень вместо сложения и деления:

${ displaystyle { sqrt [{n}] {x_ {1} cdot x_ {2} cdots x_ {n}}}.}.$

Если Икс₁, Икс₂, . . . , Икс_п > 0, это равно экспоненциальный среднего арифметического натуральные логарифмы номеров:

${ displaystyle exp left ({ frac { ln {x_ {1}} + ln {x_ {2}} + cdots + ln {x_ {n}}} {n}} right). }$

Неравенство

Повторяя неравенство с использованием математических обозначений, мы имеем это для любого списка п неотрицательные действительные числа Икс₁, Икс₂, . . . , Икс_п,

${ displaystyle { frac {x_ {1} + x_ {2} + cdots + x_ {n}} {n}} geq { sqrt [{n}] {x_ {1} cdot x_ {2}) cdots x_ {n}}} ,,}$

и это равенство выполняется тогда и только тогда, когда Икс₁ = Икс₂ = · · · = Икс_п.

Геометрическая интерпретация

В двух измерениях, 2Икс₁ + 2Икс₂ это периметр прямоугольника со сторонами длиныИкс₁ иИкс₂. По аналогии, 4√Икс₁Икс₂ периметр квадрата с таким же площадь, Икс₁Икс₂, как этот прямоугольник. Таким образом, для п = 2 неравенство AM – GM гласит, что прямоугольник заданной области имеет наименьший периметр, если этот прямоугольник также является квадратом.

Полное неравенство является расширением этой идеи на п размеры. Каждая вершина п-габаритная коробка подключена к п края. Если длины этих ребер равны Икс₁, Икс₂, . . . , Икс_п, тогда Икс₁ + Икс₂ + · · · + Икс_п - общая длина ребер, инцидентных вершине. Есть 2^п вершины, поэтому мы умножаем это на2^п; однако, поскольку каждое ребро пересекает две вершины, каждое ребро считается дважды. Поэтому делим на2 и делаем вывод, что есть 2^п−1п края. Равное количество краев каждой длины и п длины; следовательно, есть 2^п−1 кромок каждой длины, а сумма всех длин кромок равна 2^п−1(Икс₁ + Икс₂ + · · · + Икс_п). С другой стороны,

${ displaystyle 2 ^ {n-1} (x_ {1} + ldots + x_ {n}) = 2 ^ {n-1} n { sqrt [{n}] {x_ {1} x_ {2} cdots x_ {n}}}}$

- общая длина ребер, соединенных с вершиной на п-мерный куб равного объема, так как в данном случае Икс₁=...=Икс_п. Поскольку неравенство говорит

${ Displaystyle {x_ {1} + x_ {2} + cdots + x_ {n} over n} geq { sqrt [{n}] {x_ {1} x_ {2} cdots x_ {n}) }},}$

его можно пересчитать, умножив на п2^п–1 чтобы получить

${ displaystyle 2 ^ {n-1} (x_ {1} + x_ {2} + cdots + x_ {n}) geq 2 ^ {n-1} n { sqrt [{n}] {x_ { 1} x_ {2} cdots x_ {n}}}}$

с равенством тогда и только тогда, когда Икс₁ = Икс₂ = · · · = Икс_п.

Таким образом, неравенство AM – GM утверждает, что только п-куб имеет наименьшую сумму длин ребер, соединенных с каждой вершиной среди всех п-габаритные коробки такого же объема.^[2]

Пример приложения

Рассмотрим функцию

${ displaystyle f (x, y, z) = { frac {x} {y}} + { sqrt { frac {y} {z}}} + { sqrt [{3}] { frac { z} {x}}}}$

для всех положительных действительных чисел Икс, у иz. Предположим, мы хотим найти минимальное значение этой функции. Сначала немного перепишем:

${ displaystyle { begin {align} f (x, y, z) & = 6 cdot { frac {{ frac {x} {y}} + { frac {1} {2}} { sqrt { frac {y} {z}}} + { frac {1} {2}} { sqrt { frac {y} {z}}} + { frac {1} {3}} { sqrt [{3}] { frac {z} {x}}} + { frac {1} {3}} { sqrt [{3}] { frac {z} {x}}} + { frac {1} {3}} { sqrt [{3}] { frac {z} {x}}}} {6}} & = 6 cdot { frac {x_ {1} + x_ {2 } + x_ {3} + x_ {4} + x_ {5} + x_ {6}} {6}} end {align}}}$

с

${ displaystyle x_ {1} = { frac {x} {y}}, qquad x_ {2} = x_ {3} = { frac {1} {2}} { sqrt { frac {y} {z}}}, qquad x_ {4} = x_ {5} = x_ {6} = { frac {1} {3}} { sqrt [{3}] { frac {z} {x} }}.}$

Применяя неравенство AM – GM для п = 6, мы получили

${ Displaystyle { begin {align} f (x, y, z) & geq 6 cdot { sqrt [{6}] {{ frac {x} {y}} cdot { frac {1} {2}} { sqrt { frac {y} {z}}} cdot { frac {1} {2}} { sqrt { frac {y} {z}}} cdot { frac { 1} {3}} { sqrt [{3}] { frac {z} {x}}} cdot { frac {1} {3}} { sqrt [{3}] { frac {z } {x}}} cdot { frac {1} {3}} { sqrt [{3}] { frac {z} {x}}}}} & = 6 cdot { sqrt [ {6}] {{ frac {1} {2 cdot 2 cdot 3 cdot 3 cdot 3}} { frac {x} {y}} { frac {y} {z}} { frac {z} {x}}}} & = 2 ^ {2/3} cdot 3 ^ {1/2}. end {align}}}$

Кроме того, мы знаем, что две стороны равны именно тогда, когда все члены среднего равны:

${ displaystyle f (x, y, z) = 2 ^ {2/3} cdot 3 ^ {1/2} quad { mbox {when}} quad { frac {x} {y}} = { frac {1} {2}} { sqrt { frac {y} {z}}} = { frac {1} {3}} { sqrt [{3}] { frac {z} { Икс}}}.}$

Все точки (Икс, у, z) удовлетворяющие этим условиям, лежат на полуоси, начинающейся в начале координат, и имеют вид

${ displaystyle (x, y, z) = { biggr (} t, { sqrt [{3}] {2}} { sqrt {3}} , t, { frac {3 { sqrt { 3}}} {2}} , t { biggr)} quad { mbox {with}} quad t> 0.}$

Практическое применение

Важное практическое применение в финансовая математика заключается в вычислении норма прибыли: the годовая прибыль, рассчитанная с помощью среднего геометрического, меньше средней годовой прибыли, рассчитанной по среднему арифметическому (или равной, если все доходы равны). Это важно при анализе инвестиций, так как средний доход превышает совокупный эффект.

Доказательства неравенства AM – GM.

Доказательство с использованием неравенства Дженсена

Неравенство Дженсена заявляет, что значение вогнутая функция среднего арифметического больше или равно среднему арифметическому значений функции. Поскольку логарифм функция вогнутая, имеем

${ displaystyle log left ({ frac { sum _ {i} x_ {i}} {n}} right) geq sum { frac {1} {n}} log x_ {i} = sum left ( log x_ {i} ^ {1 / n} right) = log left ( prod x_ {i} ^ {1 / n} right).}$

Принимая антилоги крайних левых и крайних правых частей имеем неравенство AM – GM.

Доказательства по индукции

Мы должны показать, что

${ Displaystyle { frac {x_ {1} + x_ {2} + cdots + x_ {n}} {n}} geq { sqrt [{n}] {x_ {1} x_ {2} cdots x_ {n}}}}$

с равенством только тогда, когда все числа равны. Если Икс_я ≠ Икс_j, а затем заменив оба Икс_я и Икс_j к(Икс_я + Икс_j)/2 оставит среднее арифметическое в левой части без изменений, но увеличит среднее геометрическое в правой части, потому что

${ displaystyle { Bigl (} { frac {x_ {i} + x_ {j}} {2}} { Bigr)} ^ {2} -x_ {i} x_ {j} = { Bigl (} { frac {x_ {i} -x_ {j}} {2}} { Bigr)} ^ {2}> 0.}$

Таким образом, правая часть будет наибольшей, когда все Икс_яs равны среднему арифметическому

${ displaystyle alpha = { frac {x_ {1} + x_ {2} + cdots + x_ {n}} {n}},}$

таким образом, поскольку это наибольшее значение правой части выражения, мы имеем

${ displaystyle { frac {x_ {1} + x_ {2} + cdots + x_ {n}} {n}} = alpha = { sqrt [{n}] { alpha alpha cdots alpha }} geq { sqrt [{n}] {x_ {1} x_ {2} cdots x_ {n}}}.}.}$

Это веское доказательство по делу п = 2, но процедура итеративного попарного усреднения может не дать п равные числа в случае п ≥ 3. Примером этого случая является Икс₁ = Икс₂ ≠ Икс₃: Усреднение двух разных чисел дает два равных числа, но третье по-прежнему отличается. Следовательно, на самом деле мы никогда не получим неравенство, включающее среднее геометрическое трех равных чисел.

Следовательно, необходим дополнительный трюк или модифицированный аргумент, чтобы превратить вышеупомянутую идею в действительное доказательство для случая п ≥ 3.

Доказательство по индукции # 1.

Из неотрицательных действительных чисел Икс₁, . . . , Икс_п, утверждение AM – GM эквивалентно

${ Displaystyle альфа ^ {п} geq x_ {1} x_ {2} cdots x_ {n}}$

с равенством тогда и только тогда, когда α = Икс_я для всех я ∈ {1, . . . , п}.

Для следующего доказательства применим математическая индукция и только общеизвестные правила арифметики.

Индукционная основа: За п = 1 утверждение верно с равенством.

Гипотеза индукции: Предположим, что утверждение AM – GM выполняется для любого выбора п неотрицательные действительные числа.

Шаг индукции: Учитывать п + 1 неотрицательные действительные числа Икс₁, . . . , Икс_п+1,. Их среднее арифметическое α удовлетворяет

${ displaystyle (n + 1) alpha = x_ {1} + cdots + x_ {n} + x_ {n + 1}.}$

Если все Икс_я равны α, то мы имеем равенство в утверждении AM – GM, и все готово. В случае, если некоторые из них не равны α, должно существовать одно число, которое больше среднего арифметического α, и тот, который меньше, чем α. Без потери общности мы можем изменить порядок наших Икс_я чтобы разместить эти два конкретных элемента в конце: Икс_п > α и Икс_п+1 < α. потом

${ displaystyle x_ {n} - alpha> 0 qquad alpha -x_ {n + 1}> 0}$

${ displaystyle подразумевает (x_ {n} - alpha) ( alpha -x_ {n + 1})> 0 ,. qquad (*)}$

Теперь определим у с

${ displaystyle y: = x_ {n} + x_ {n + 1} - alpha geq x_ {n} - alpha> 0 ,,}$

и рассмотрим п числа Икс₁, . . . , Икс_п–1, y которые все неотрицательны. С

${ Displaystyle (п + 1) альфа = x_ {1} + cdots + x_ {n-1} + x_ {n} + x_ {n + 1}}$

${ Displaystyle п альфа = x_ {1} + cdots + x_ {n-1} + underbrace {x_ {n} + x_ {n + 1} - alpha} _ {= , y},}$

Таким образом, α также является средним арифметическим п числа Икс₁, . . . , Икс_п–1, у а из предположения индукции следует

${ displaystyle alpha ^ {n + 1} = alpha ^ {n} cdot alpha geq x_ {1} x_ {2} cdots x_ {n-1} y cdot alpha. qquad (* *)}$

Благодаря (*) мы знаем, что

${ displaystyle ( underbrace {x_ {n} + x_ {n + 1} - alpha} _ {= , y}) alpha -x_ {n} x_ {n + 1} = (x_ {n} - alpha) ( alpha -x_ {n + 1})> 0,}$

следовательно

${ Displaystyle у альфа> х_ {п} х_ {п + 1} ,, qquad ({*} {*} {*})}$

особенно α > 0. Следовательно, если хотя бы одно из чисел Икс₁, . . . , Икс_п–1 равен нулю, то строгое неравенство в (**) уже выполняется. В противном случае правая часть (**) положительна, и строгое неравенство получается путем использования оценки (***) для получения нижней оценки правой части (**). Таким образом, в обоих случаях мы можем заменить (***) на (**), чтобы получить

${ Displaystyle альфа ^ {п + 1}> x_ {1} x_ {2} cdots x_ {n-1} x_ {n} x_ {n + 1} ,,}$

что завершает доказательство.

Доказательство по индукции # 2.

Прежде всего докажем, что для действительных чисел Икс₁ < 1 и Икс₂ > 1 там следует

${ displaystyle x_ {1} + x_ {2}> x_ {1} x_ {2} +1.}$

Действительно, умножая обе части неравенства Икс₂ > 1 к 1 – Икс₁, дает

${ displaystyle x_ {2} -x_ {1} x_ {2}> 1-x_ {1},}$

откуда сразу получается требуемое неравенство.

Теперь мы собираемся доказать, что для положительных действительных чисел Икс₁, . . . , Икс_п удовлетворениеИкс₁ . . . Икс_п = 1, там держит

${ displaystyle x_ {1} + cdots + x_ {n} geq n.}$

Равенство выполняется, только если Икс₁ = ... = Икс_п = 1.

Индукционная основа: За п = 2 утверждение верно из-за вышеуказанного свойства.

Гипотеза индукции: Предположим, что утверждение верно для всех натуральных чисел до п – 1.

Шаг индукции: Рассмотрим натуральное число п, т.е. для положительных действительных чисел Икс₁, . . . , Икс_п, там держит Икс₁ . . . Икс_п = 1. Есть хотя бы один Икс_k < 1, поэтому должен быть хотя бы один Икс_j > 1. Без ограничения общности положим k =п – 1 и j = п.

Далее, равенство Икс₁ . . . Икс_п = 1 мы будем писать в виде (Икс₁ . . . Икс_п–2) (Икс_п–1 Икс_п) = 1. Тогда из предположения индукции следует

${ displaystyle (x_ {1} + cdots + x_ {n-2}) + (x_ {n-1} x_ {n})> n-1.}$

Однако с учетом базиса индукции имеем

${ displaystyle { begin {align} x_ {1} + cdots + x_ {n-2} + x_ {n-1} + x_ {n} & = (x_ {1} + cdots + x_ {n- 2}) + (x_ {n-1} + x_ {n}) &> (x_ {1} + cdots + x_ {n-2}) + x_ {n-1} x_ {n} +1 &> n, end {выровнено}}}$

что завершает доказательство.

Для положительных вещественных чисел а₁, . . . , а_п, обозначим

${ displaystyle x_ {1} = { frac {a_ {1}} { sqrt [{n}] {a_ {1} cdots a_ {n}}}}, ..., x_ {n} = { frac {a_ {n}} { sqrt [{n}] {a_ {1} cdots a_ {n}}}}.}$

Цифры Икс₁, . . . , Икс_п удовлетворять условию Икс₁ . . . Икс_п = 1. Итак, у нас есть

${ displaystyle { frac {a_ {1}} { sqrt [{n}] {a_ {1} cdots a_ {n}}}} + cdots + { frac {a_ {n}} { sqrt [{n}] {a_ {1} cdots a_ {n}}}} geq n,}$

откуда получаем

${ displaystyle { frac {a_ {1} + cdots + a_ {n}} {n}} geq { sqrt [{n}] {a_ {1} cdots a_ {n}}},}$

с равенством только для а₁ = ... = а_п.

Доказательство Коши с использованием индукции вперед – назад.

Следующее ниже доказательство по случаям напрямую опирается на хорошо известные правила арифметики, но использует редко используемую технику прямой-обратной индукции. По сути, это из Огюстен Луи Коши и можно найти в его Cours d'analyse.^[3]

Случай, когда все члены равны

Если все условия равны:

${ Displaystyle x_ {1} = x_ {2} = cdots = x_ {n},}$

тогда их сумма nx₁, поэтому их среднее арифметическоеИкс₁; и их продукт Икс₁^п, поэтому их среднее геометрическоеИкс₁; следовательно, среднее арифметическое и среднее геометрическое равны, как требуется.

Случай, когда не все члены равны

Осталось показать, что если нет все члены равны, то среднее арифметическое больше среднего геометрического. Ясно, что это возможно только тогда, когда п > 1.

Этот случай значительно сложнее, и мы разбиваем его на подслучаи.

Подслучай, где п = 2

Если п = 2, то у нас есть два члена, Икс₁ и Икс₂, а поскольку (по нашему предположению) не все члены равны, имеем:

${ displaystyle { begin {align} { Bigl (} { frac {x_ {1} + x_ {2}} {2}} { Bigr)} ^ {2} -x_ {1} x_ {2} & = { frac {1} {4}} (x_ {1} ^ {2} + 2x_ {1} x_ {2} + x_ {2} ^ {2}) - x_ {1} x_ {2} & = { frac {1} {4}} (x_ {1} ^ {2} -2x_ {1} x_ {2} + x_ {2} ^ {2}) & = { Bigl (} { frac {x_ {1} -x_ {2}} {2}} { Bigr)} ^ {2}> 0, end {выравнивается}}}$

следовательно

${ displaystyle { frac {x_ {1} + x_ {2}} {2}}> { sqrt {x_ {1} x_ {2}}}}$

по желанию.

Подслучай, где п = 2^k

Рассмотрим случай, когда п = 2^k, куда k положительное целое число. Действуем по математической индукции.

В базовом случае k = 1, так п = 2. Мы уже показали, что неравенство выполняется при п = 2Итак, мы закончили.

Теперь предположим, что для данного k > 1, мы уже показали, что неравенство выполняется для п = 2^k−1, и мы хотим показать, что это справедливо для п = 2^k. Для этого дважды применим неравенство для 2^k-1 числа и один раз для 2 числа для получения:

${ displaystyle { begin {align} { frac {x_ {1} + x_ {2} + cdots + x_ {2 ^ {k}}} {2 ^ {k}}} & {} = { frac {{ frac {x_ {1} + x_ {2} + cdots + x_ {2 ^ {k-1}}} {2 ^ {k-1}}} + { frac {x_ {2 ^ {k -1} +1} + x_ {2 ^ {k-1} +2} + cdots + x_ {2 ^ {k}}} {2 ^ {k-1}}}} {2}} [ 7pt] & geq { frac {{ sqrt [{2 ^ {k-1}}] {x_ {1} x_ {2} cdots x_ {2 ^ {k-1}}}} + { sqrt [{2 ^ {k-1}}] {x_ {2 ^ {k-1} +1} x_ {2 ^ {k-1} +2} cdots x_ {2 ^ {k}}}}} { 2}} [7pt] & geq { sqrt {{ sqrt [{2 ^ {k-1}}] {x_ {1} x_ {2} cdots x_ {2 ^ {k-1}} }} { sqrt [{2 ^ {k-1}}] {x_ {2 ^ {k-1} +1} x_ {2 ^ {k-1} +2} cdots x_ {2 ^ {k} }}}}} [7pt] & = { sqrt [{2 ^ {k}}] {x_ {1} x_ {2} cdots x_ {2 ^ {k}}}} end {выровнено} }}$

где в первом неравенстве две стороны равны, только если

${ Displaystyle x_ {1} = x_ {2} = cdots = x_ {2 ^ {k-1}}}$

и

${ Displaystyle x_ {2 ^ {k-1} +1} = x_ {2 ^ {k-1} +2} = cdots = x_ {2 ^ {k}}}$

(в этом случае первое среднее арифметическое и первое среднее геометрическое равныИкс₁, и аналогично со вторым средним арифметическим и вторым средним геометрическим); а во втором неравенстве две стороны равны, только если два геометрических средних равны. Поскольку не все 2^k числа равны, оба неравенства не могут быть равенствами, поэтому мы знаем, что:

${ displaystyle { frac {x_ {1} + x_ {2} + cdots + x_ {2 ^ {k}}} {2 ^ {k}}}> { sqrt [{2 ^ {k}}] {x_ {1} x_ {2} cdots x_ {2 ^ {k}}}}}$

по желанию.

Подслучай, где п < 2^k

Если п это не естественная сила2, то конечно меньше чем некоторая естественная степень двойки, поскольку последовательность 2, 4, 8, . . . , 2^k, . . . неограничен сверху. Поэтому без ограничения общности пусть м быть какой-то естественной силой 2 это больше, чемп.

Итак, если у нас есть п терминов, то обозначим их среднее арифметическое черезα, и расширите наш список терминов следующим образом:

${ displaystyle x_ {n + 1} = x_ {n + 2} = cdots = x_ {m} = alpha.}$

Тогда у нас есть:

${ displaystyle { begin {align} alpha & = { frac {x_ {1} + x_ {2} + cdots + x_ {n}} {n}} [6pt] & = { frac { { frac {m} {n}} left (x_ {1} + x_ {2} + cdots + x_ {n} right)} {m}} [6pt] & = { frac {x_ {1} + x_ {2} + cdots + x_ {n} + { frac {(mn)} {n}} left (x_ {1} + x_ {2} + cdots + x_ {n} right)} {m}} [6pt] & = { frac {x_ {1} + x_ {2} + cdots + x_ {n} + left (mn right) alpha} {m}} [6pt] & = { frac {x_ {1} + x_ {2} + cdots + x_ {n} + x_ {n + 1} + cdots + x_ {m}} {m}} [6pt] &> { sqrt [{m}] {x_ {1} x_ {2} cdots x_ {n} x_ {n + 1} cdots x_ {m}}} [6pt] & = { sqrt [{m}] {x_ {1} x_ {2} cdots x_ {n} alpha ^ {mn}}} ,, end {выровнено}}}$

так

${ displaystyle alpha ^ {m}> x_ {1} x_ {2} cdots x_ {n} alpha ^ {m-n}}$

и

${ displaystyle alpha> { sqrt [{n}] {x_ {1} x_ {2} cdots x_ {n}}}}$

по желанию.

Доказательство по индукции с использованием основного исчисления.

Следующее доказательство использует математическую индукцию и некоторые основные дифференциальное исчисление.

Индукционная основа: За п = 1 утверждение верно с равенством.

Гипотеза индукции: Предположим, что утверждение AM – GM выполняется для любого выбора п неотрицательные действительные числа.

Индукционный шаг: Чтобы доказать утверждение для п + 1 неотрицательные действительные числа Икс₁, . . . , Икс_п, Икс_п+1, нам нужно доказать, что

${ displaystyle { frac {x_ {1} + cdots + x_ {n} + x_ {n + 1}} {n + 1}} - ({x_ {1} cdots x_ {n} x_ {n + 1}}) ^ { frac {1} {n + 1}} geq 0}$

с равенством, только если все п + 1 числа равны.

Если все числа равны нулю, неравенство выполняется с равенством. Если некоторые, но не все числа равны нулю, мы имеем строгое неравенство. Поэтому в дальнейшем можно считать, что все п + 1 числа положительные.

Считаем последний номер Икс_п+1 как переменную и определите функцию

${ displaystyle f (t) = { frac {x_ {1} + cdots + x_ {n} + t} {n + 1}} - ({x_ {1} cdots x_ {n} t}) ^ { frac {1} {n + 1}}, qquad t> 0.}$

Доказательство шага индукции эквивалентно доказательству того, что ж(т) ≥ 0 для всех т > 0, с ж(т) = 0 только если Икс₁, . . . , Икс_п ит все равны. Это можно сделать, проанализировав критические точки изж используя некоторые базовые вычисления.

Первый производная из ж дан кем-то

${ displaystyle f '(t) = { frac {1} {n + 1}} - { frac {1} {n + 1}} ({x_ {1} cdots x_ {n}}) ^ { frac {1} {n + 1}} t ^ {- { frac {n} {n + 1}}}, qquad t> 0.}$

Критическая точка т₀ должен удовлетворить f ′(т₀) = 0, что значит

${ displaystyle ({x_ {1} cdots x_ {n}}) ^ { frac {1} {n + 1}} t_ {0} ^ {- { frac {n} {n + 1}}} = 1.}$

После небольшой переделки получаем

${ displaystyle t_ {0} ^ { frac {n} {n + 1}} = ({x_ {1} cdots x_ {n}}) ^ { frac {1} {n + 1}},}$

и наконец

${ displaystyle t_ {0} = ({x_ {1} cdots x_ {n}}) ^ { frac {1} {n}},}$

что является средним геометрическим Икс₁, . . . , Икс_п. Это единственная критическая точкаж. С f ′ ′(т) > 0 для всех т > 0, функцияж является строго выпуклый и имеет строгий глобальный минимум вт₀. Затем мы вычисляем значение функции в этом глобальном минимуме:

${ displaystyle { begin {align} f (t_ {0}) & = { frac {x_ {1} + cdots + x_ {n} + ({x_ {1} cdots x_ {n}}) ^ {1 / n}} {n + 1}} - ({x_ {1} cdots x_ {n}}) ^ { frac {1} {n + 1}} ({x_ {1} cdots x_ { n}}) ^ { frac {1} {n (n + 1)}} & = { frac {x_ {1} + cdots + x_ {n}} {n + 1}} + { гидроразрыв {1} {n + 1}} ({x_ {1} cdots x_ {n}}) ^ { frac {1} {n}} - ({x_ {1} cdots x_ {n}}) ^ { frac {1} {n}} & = { frac {x_ {1} + cdots + x_ {n}} {n + 1}} - { frac {n} {n + 1} } ({x_ {1} cdots x_ {n}}) ^ { frac {1} {n}} & = { frac {n} {n + 1}} { Bigl (} { frac {x_ {1} + cdots + x_ {n}} {n}} - ({x_ {1} cdots x_ {n}}) ^ { frac {1} {n}} { Bigr)} & geq 0, end {выровнено}}}$

где последнее неравенство выполняется в силу предположения индукции. Гипотеза также гласит, что равенство может быть только тогда, когда Икс₁, . . . , Икс_п все равны. В этом случае их среднее геометрическоет₀ имеет то же значение, следовательно, если Икс₁, . . . , Икс_п, Икс_п+1 все равны, у нас есть ж(Икс_п+1) > 0. Это завершает доказательство.

Таким же образом можно использовать эту технику для доказательства обобщенного неравенства AM – GM и Неравенство Коши – Шварца в евклидовом пространстве р^п.

Доказательство Полиа с использованием экспоненциальной функции

Георгий Полиа предоставил доказательство, подобное следующему. Позволять ж(Икс) = е^Икс–1 – Икс для всех реальныхИкс, с первым производная f ′(Икс) = е^Икс–1 – 1 и вторая производная f ′ ′(Икс) = е^Икс–1. Заметьте, что ж(1) = 0, f ′(1) = 0 и f ′ ′(Икс) > 0 для всех реальныхИкс, следовательно ж строго выпуклая с абсолютным минимумом при Икс = 1. Следовательно Икс ≤ e^Икс–1 для всех реальныхИкс с равенством только для Икс = 1.

Рассмотрим список неотрицательных действительных чисел Икс₁, Икс₂, . . . , Икс_п. Если все они равны нулю, то неравенство AM – GM выполняется с равенством. Следовательно, в дальнейшем мы можем принять за их среднее арифметическое α > 0. К п-кратно применяя полученное неравенство, получаем, что

${ displaystyle { begin {align} {{ frac {x_ {1}} { alpha}} { frac {x_ {2}} { alpha}} cdots { frac {x_ {n}} { alpha}}} & leq {e ^ {{ frac {x_ {1}} { alpha}} - 1} e ^ {{ frac {x_ {2}} { alpha}} - 1} cdots e ^ {{ frac {x_ {n}} { alpha}} - 1}} & = exp { Bigl (} { frac {x_ {1}} { alpha}} - 1+ { frac {x_ {2}} { alpha}} - 1+ cdots + { frac {x_ {n}} { alpha}} - 1 { Bigr)}, qquad (*) end { выровнено}}}$

с равенством тогда и только тогда, когда Икс_я = α для каждого я ∈ {1, . . . , п}. Аргумент экспоненциальной функции можно упростить:

${ displaystyle { begin {align} { frac {x_ {1}} { alpha}} - 1 + { frac {x_ {2}} { alpha}} - 1+ cdots + { frac { x_ {n}} { alpha}} - 1 & = { frac {x_ {1} + x_ {2} + cdots + x_ {n}} { alpha}} - n & = { frac { n alpha} { alpha}} - n & = 0. end {align}}}$

Возвращаясь к (*),

${ displaystyle { frac {x_ {1} x_ {2} cdots x_ {n}} { alpha ^ {n}}} leq e ^ {0} = 1,}$

который производит Икс₁ Икс₂ · · · Икс_п ≤ α^п, отсюда результат^[4]

${ displaystyle { sqrt [{n}] {x_ {1} x_ {2} cdots x_ {n}}} leq alpha.}$

Доказательство с помощью лагранжевых множителей.

Если любой из ${ displaystyle x_ {i}}$ находятся ${ displaystyle 0}$, то доказывать нечего. Таким образом, мы можем предположить, что все ${ displaystyle x_ {i}}$ строго положительные.

Поскольку средние арифметические и геометрические однородны степени 1, без ограничения общности предположим, что ${ Displaystyle prod _ {я = 1} ^ {п} х_ {я} = 1}$. Набор ${ Displaystyle G (x_ {1}, x_ {2}, ldots, x_ {n}) = prod _ {i = 1} ^ {n} x_ {i}}$, и ${ Displaystyle F (x_ {1}, x_ {2}, ldots, x_ {n}) = { frac {1} {n}} sum _ {i = 1} ^ {n} x_ {i} }$. Неравенство будет доказано (вместе со случаем равенства), если мы сможем показать, что минимум ${ Displaystyle F (x_ {1}, x_ {2}, ..., x_ {n}),}$ при условии ограничения ${ Displaystyle G (x_ {1}, x_ {2}, ldots, x_ {n}) = 1,}$ равно ${ displaystyle 1}$, а минимум достигается только при ${ Displaystyle x_ {1} = x_ {2} = cdots = x_ {n} = 1}$. Сначала покажем, что задача условной минимизации имеет глобальный минимум.

Набор ${ Displaystyle К = {(x_ {1}, x_ {2}, ldots, x_ {n}) двоеточие 0 leq x_ {1}, x_ {2}, ldots, x_ {n} leq п }}$. Поскольку пересечение ${ Displaystyle К крышка {G = 1 }}$ компактна, теорема об экстремальном значении гарантирует, что минимум ${ Displaystyle F (x_ {1}, x_ {2}, ..., x_ {n})}$ с учетом ограничений ${ Displaystyle G (x_ {1}, x_ {2}, ldots, x_ {n}) = 1}$ и ${ displaystyle (x_ {1}, x_ {2}, ldots, x_ {n}) in K}$ достигается в какой-то момент внутри ${ displaystyle K}$. С другой стороны, обратите внимание, что если любой из ${ displaystyle x_ {i}> n}$, тогда ${ Displaystyle F (x_ {1}, x_ {2}, ldots, x_ {n})> 1}$, пока ${ Displaystyle F (1,1, ldots, 1) = 1}$, и ${ Displaystyle (1,1, ldots, 1) в K cap {G = 1 }}$. Это означает, что минимум внутри ${ Displaystyle К крышка {G = 1 }}$ фактически является глобальным минимумом, так как значение ${ displaystyle F}$ в любой точке внутри ${ Displaystyle К крышка {G = 1 }}$ конечно не меньше минимума, а значение ${ displaystyle F}$ в любой момент ${ displaystyle (y_ {1}, y_ {2}, ldots, y_ {n})}$ не внутри ${ displaystyle K}$ строго больше, чем значение при ${ Displaystyle (1,1, ldots, 1)}$, что не меньше минимального.

Методика Множители Лагранжа говорит, что глобальный минимум достигается в точке ${ displaystyle (x_ {1}, x_ {2}, ldots, x_ {n})}$ где градиент ${ Displaystyle F (x_ {1}, x_ {2}, ldots, x_ {n})}$ является ${ displaystyle lambda}$ раз градиент ${ Displaystyle G (x_ {1}, x_ {2}, ldots, x_ {n})}$, для некоторых ${ displaystyle lambda}$. Мы покажем, что это происходит только тогда, когда ${ Displaystyle x_ {1} = x_ {2} = cdots = x_ {n} = 1}$ и ${ displaystyle F (x_ {1}, x_ {2}, ..., x_ {n}) = 1.}$

Вычислить ${ displaystyle { frac { partial F} { partial x_ {i}}} = { frac {1} {n}}}$ и

${ displaystyle { frac { partial G} { partial x_ {i}}} = prod _ {j neq i} x_ {j} = { frac {G (x_ {1}, x_ {2}) , ldots, x_ {n})} {x_ {i}}} = { frac {1} {x_ {i}}}}$

по ограничению. Таким образом, установка градиентов, пропорциональных друг другу, дает для каждого ${ displaystyle i}$ который ${ displaystyle { frac {1} {n}} = { frac { lambda} {x_ {i}}},}$ и так ${ displaystyle n lambda = x_ {i}.}$ Поскольку левая часть не зависит от ${ displaystyle i}$, следует, что ${ Displaystyle x_ {1} = x_ {2} = cdots = x_ {n}}$, и с тех пор ${ Displaystyle G (x_ {1}, x_ {2}, ldots, x_ {n}) = 1}$, следует, что ${ Displaystyle x_ {1} = x_ {2} = cdots = x_ {n} = 1}$ и ${ Displaystyle F (x_ {1}, x_ {2}, ldots, x_ {n}) = 1}$, по желанию.

Обобщения

Весовое неравенство AM – GM.

Аналогичное неравенство имеется для средневзвешенное арифметическое и средневзвешенное геометрическое. В частности, пусть неотрицательные числа Икс₁, Икс₂, . . . , Икс_п и неотрицательные веса ш₁, ш₂, . . . , ш_п быть данным. Набор ш = ш₁ + ш₂ + · · · + ш_п. Еслиш > 0, то неравенство

${ displaystyle { frac {w_ {1} x_ {1} + w_ {2} x_ {2} + cdots + w_ {n} x_ {n}} {w}} geq { sqrt [{w} ] {x_ {1} ^ {w_ {1}} x_ {2} ^ {w_ {2}} cdots x_ {n} ^ {w_ {n}}}}}$

выполняется с равенством тогда и только тогда, когда все Икс_k с ш_k > 0 равны. Здесь условность 0⁰ = 1 используется.

Я упал ш_k = 1, это сводится к рассмотренному выше неравенству средних арифметических и геометрических.

Доказательство с использованием неравенства Дженсена

Используя конечную форму Неравенство Дженсена для натуральный логарифм, мы можем доказать неравенство между взвешенным средним арифметическим и средневзвешенным геометрическим, указанное выше.

Поскольку Икс_k с весом ш_k = 0 не влияет на неравенство, в дальнейшем мы можем предполагать, что все веса положительны. Я упал Икс_k равны, то выполняется равенство. Следовательно, остается доказать строгое неравенство, если не все они равны, что мы и будем предполагать в дальнейшем. Если хотя бы один Икс_k равно нулю (но не всем), то средневзвешенное геометрическое среднее равно нулю, а средневзвешенное арифметическое положительно, следовательно, выполняется строгое неравенство. Поэтому можно также считать, что все Икс_k положительные.

Поскольку натуральный логарифм равен строго вогнутый, конечный вид неравенства Йенсена и функциональные уравнения натурального логарифма следует

${ displaystyle { begin {align} ln { Bigl (} { frac {w_ {1} x_ {1} + cdots + w_ {n} x_ {n}} {w}} { Bigr)} &> { frac {w_ {1}} {w}} ln x_ {1} + cdots + { frac {w_ {n}} {w}} ln x_ {n} & = ln { sqrt [{w}] {x_ {1} ^ {w_ {1}} x_ {2} ^ {w_ {2}} cdots x_ {n} ^ {w_ {n}}}}. end { выровнено}}}$

Поскольку натуральный логарифм равен строго возрастающий,

${ displaystyle { frac {w_ {1} x_ {1} + cdots + w_ {n} x_ {n}} {w}}> { sqrt [{w}] {x_ {1} ^ {w_ { 1}} x_ {2} ^ {w_ {2}} cdots x_ {n} ^ {w_ {n}}}}.}.$

Матричное арифметическое среднее геометрическое неравенство

Большинство матричных обобщений неравенства среднего геометрического применяется на уровне унитарно-инвариантных норм в силу того факта, что даже если матрицы ${ displaystyle A}$ и ${ displaystyle B}$ положительно полуопределены матрица ${ displaystyle AB}$ не может быть положительным полуопределенным и, следовательно, может не иметь канонического квадратного корня. В ^[5] Бхатиа и Киттане доказали, что для любой унитарно инвариантной нормы ${ Displaystyle ||| cdot |||}$ и положительно полуопределенные матрицы ${ displaystyle A}$ и ${ displaystyle B}$ это тот случай, когда

${ displaystyle ||| AB ||| leq { frac {1} {2}} ||| A ^ {2} + B ^ {2} |||}$

Позже ^[6] те же авторы доказали более сильное неравенство, что

${ displaystyle ||| AB ||| leq { frac {1} {4}} ||| (A + B) ^ {2} |||}$

Наконец, известен размерностью ${ displaystyle n = 2}$ что справедливо следующее наиболее сильное матричное обобщение неравенства среднего арифметико-геометрического, и предполагается, что оно справедливо для всех ${ displaystyle n}$

${ displaystyle ||| (AB) ^ { frac {1} {2}} ||| leq { frac {1} {2}} ||| A + B |||}$

Другие обобщения

Геометрический доказательство без слов который Максимум (а,б) > среднее квадратичное или же среднеквадратичное значение (QM) > среднее арифметическое (ЯВЛЯЮСЬ) > среднее геометрическое (GM) > гармоническое среднее (HM) > мин (а,б) двух положительных чисел а и б ^[7]

Другие обобщения неравенства средних арифметических и геометрических включают:

• Неравенство Мюрхеда,
• Неравенство Маклорена,
• Обобщенное среднее неравенство.

Смотрите также

• Загадка упаковки Хоффмана
• Кай Фань неравенство
• Неравенство Юнга для продуктов

Примечания

Новые неравенства с классическими средними появились в ряде публикаций (см. [7]).

Рекомендации

 7. Флорин Ничита, О классическом неравенстве средств, Энциклопедия научного сообщества, MDPI, https://encyclopedia.pub/2364 - Создано: 20 августа 2020 г .; Обновлено: 20 авг.2020 г.

внешняя ссылка

• Артур Лохуотер (1982). «Введение в неравенство». Электронная книга в формате PDF.