WikiDer > Среднеквадратичное значение

Root mean square

В математика и его приложений, среднеквадратичное значение (RMS или же среднеквадратичное значение) определяется как квадратный корень из средний квадрат (в среднее арифметическое из квадраты из набор номеров).^[1]RMS также известен как среднее квадратичное^[2]^[3] и является частным случаем обобщенное среднее с показателем 2. RMS также можно определить для непрерывно меняющейся функция с точки зрения интеграл квадратов мгновенных значений за цикл.

За переменный электрический ток, RMS равно значению постоянный ток что даст такое же среднее рассеивание мощности в резистивная нагрузка.^[1]

В теория оценки, то среднеквадратичное отклонение оценщика - это мера несовершенства соответствия оценщика данным.

Определение

Среднеквадратичное значение набора значений (или непрерывное время форма волны) - это квадратный корень из среднего арифметического квадратов значений или квадрат функции, определяющей непрерывный сигнал. В физике среднеквадратичное значение тока также можно определить как «значение постоянного тока, который рассеивает ту же мощность в резисторе».

В случае набора п значения ${ displaystyle {x_ {1}, x_ {2}, dots, x_ {n} }}$ , RMS равно

{ displaystyle x _ { text {RMS}} = { sqrt {{ frac {1} {n}} left (x_ {1} ^ {2} + x_ {2} ^ {2} + cdots + x_ {n} ^ {2} right)}}.}

Соответствующая формула для непрерывной функции (или формы сигнала) ж(т), определенные на интервале ${ Displaystyle T_ {1} leq t leq T_ {2}}$ является

{ displaystyle f _ { text {RMS}} = { sqrt {{1 over {T_ {2} -T_ {1}}} { int _ {T_ {1}} ^ {T_ {2}} { [f (t)]} ^ {2} , dt}}},}

и RMS для функции за все время

{ displaystyle f _ { text {RMS}} = lim _ {T rightarrow infty} { sqrt {{1 over {T}} { int _ {0} ^ {T} {[f (t )]} ^ {2} , dt}}}.}

RMS за все время периодическая функция равно RMS одного периода функции. Среднеквадратичное значение непрерывной функции или сигнала можно приблизительно оценить, взяв среднеквадратичное значение выборки, состоящей из равноудаленных наблюдений. Кроме того, среднеквадратичное значение различных форм сигналов также может быть определено без исчисление, как показано Картрайтом.^[4]

В случае RMS-статистики случайный процесс, то ожидаемое значение используется вместо среднего.

В обычных формах волны

Синус, квадрат, треугольник, и пилообразный формы волны.

Прямоугольная импульсная волна с скважностью D, отношение длительностей импульсов (

{ Displaystyle тау}

) и период (T); проиллюстрировано здесь с а = 1.

График зависимости напряжения синусоидальной волны от времени (в градусах), показывающий среднеквадратичное, пиковое (PK) и размах напряжения (PP).

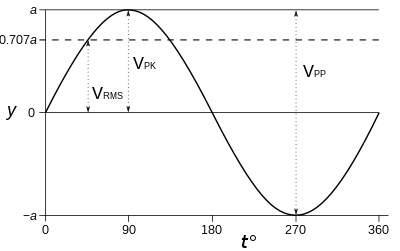
Если форма волны чистый синусоидальная волна, отношения между амплитудами (размахом, пиком) и среднеквадратичным значением фиксированы и известны, как и для любых непрерывных периодический волна. Однако это неверно для сигнала произвольной формы, который не может быть периодическим или непрерывным. Для синусоиды с нулевым средним соотношение между среднеквадратичным значением и размахом амплитуды составляет:

От пика до пика

{ displaystyle = 2 { sqrt {2}} times { text {RMS}} примерно 2,8 times { text {RMS}}.}

Для других сигналов отношения не такие же, как для синусоидальных волн. Например, для треугольной или пилообразной волны

От пика до пика

{ displaystyle = 2 { sqrt {3}} times { text {RMS}} примерно 3,5 times { text {RMS}}.}

Форма волны	Переменные и операторы	RMS
ОКРУГ КОЛУМБИЯ	${ displaystyle y = A_ {0} ,}$	${ displaystyle A_ {0} ,}$
Синусоидальная волна	${ Displaystyle у = А_ {1} грех (2 пи футов) ,}$	${ displaystyle { frac {A_ {1}} { sqrt {2}}}}$
Квадратная волна	${ displaystyle y = { begin {cases} A_ {1} & operatorname {frac} (ft) <0,5 - A_ {1} & operatorname {frac} (ft)> 0,5 end {cases}} }$	${ Displaystyle A_ {1} ,}$
Прямоугольная волна со смещением постоянного тока	${ displaystyle y = A_ {0} + { begin {cases} A_ {1} & operatorname {frac} (ft) <0,5 - A_ {1} & operatorname {frac} (ft)> 0,5 конец {case}}}$	${ displaystyle { sqrt {A_ {0} ^ {2} + A_ {1} ^ {2}}} ,}$
Модифицированная синусоида	${ displaystyle y = { begin {cases} 0 & operatorname {frac} (ft) <0,25 A_ {1} & 0,25 < operatorname {frac} (ft) <0,5 0 & 0,5 < operatorname {frac} (ft) <0,75 - A_ {1} & operatorname {frac} (ft)> 0,75 end {case}}}$	${ displaystyle { frac {A_ {1}} { sqrt {2}}}}$
Треугольная волна	${ displaystyle y = left \| 2A_ {1} operatorname {frac} (ft) -A_ {1} right \|}$	${ displaystyle A_ {1} over { sqrt {3}}}$
Пилообразная волна	${ displaystyle y = 2A_ {1} operatorname {frac} (ft) -A_ {1} ,}$	${ displaystyle A_ {1} over { sqrt {3}}}$
Пульсовая волна	${ displaystyle y = { begin {cases} A_ {1} & operatorname {frac} (ft) D end {cases}}}$	${ displaystyle A_ {1} { sqrt {D}}}$
Междуфазное напряжение	${ displaystyle y = A_ {1} sin (t) -A_ {1} sin left (t - { frac {2 pi} {3}} right) ,}$	${ displaystyle A_ {1} { sqrt { frac {3} {2}}}}$
куда: у это смещение, т время, ж частота, А_я амплитуда (пиковое значение), D это рабочий цикл или доля периода времени (1 /ж) потратил высоко, гидроразрыв (р) это дробная часть из р.

В комбинациях сигналов

Формы сигналов, полученные путем суммирования известных простых сигналов, имеют среднеквадратичное значение, которое является корнем из суммы квадратов значений среднеквадратичных значений компонентов, если формы сигналов компонентов являются ортогональный (то есть, если среднее произведение одного простого сигнала на другой равно нулю для всех пар, кроме времени самого сигнала).^[5]

{ displaystyle { text {RMS}} _ { text {Total}} = { sqrt {{ text {RMS}} _ {1} ^ {2} + { text {RMS}} _ {2} ^ {2} + cdots + { text {RMS}} _ {n} ^ {2}}}}

В качестве альтернативы, для сигналов, которые полностью положительно коррелированы или «синфазны» друг с другом, их среднеквадратичные значения суммируются напрямую.

Использует

В электротехнике

Напряжение

Частным случаем среднеквадратичного значения комбинаций форм сигналов является:^[6]

{ displaystyle { text {RMS}} _ { text {AC + DC}} = { sqrt {{ text {RMS}} _ { text {DC}} ^ {2} + { text {RMS }} _ { text {AC}} ^ {2}}}}

куда ${ displaystyle { text {RMS}} _ { text {DC}}}$ относится к постоянный ток, или среднее значение, составляющая сигнала и ${ displaystyle { text {RMS}} _ { text {AC}}}$ это переменный ток составляющая сигнала.

Средняя электрическая мощность

Инженеры-электрики часто должны знать мощность, п, рассеивается электрическое сопротивление, р. Расчет легко произвести при постоянном Текущий, я, через сопротивление. Для загрузки р Ом, мощность определяется просто как:

{ displaystyle P = I ^ {2} R.}

Однако, если сила тока зависит от времени, я(т), эту формулу необходимо расширить, чтобы отразить тот факт, что ток (и, следовательно, мгновенная мощность) меняется во времени. Если функция периодическая (например, бытовая сеть переменного тока), все же имеет смысл обсудить средний мощность, рассеиваемая с течением времени, которая рассчитывается как среднее значение рассеиваемой мощности:

{ displaystyle { begin {align} P_ {av} & = left (I (t) ^ {2} R right) _ {av} && { text {where}} left ( cdots right) _ {av} { text {обозначает временное среднее значение функции}} [3pt] & = left (I (t) ^ {2} right) _ {av} R && { text {(as} } R { text {не меняется со временем, это можно вычесть)}} [3pt] & = I _ { text {RMS}} ^ {2} R && { text {по определению среднего -квадрат}} конец {выровнено}}}

Итак, значение RMS, я_RMS, функции я(т) - постоянный ток, который дает такое же рассеяние мощности, как и усредненная по времени рассеиваемая мощность тока я(т).

Среднюю мощность также можно найти, используя тот же метод, что и в случае изменяющегося во времени Напряжение, V(т), со значением RMS V_RMS,

{ displaystyle P _ { text {Avg}} = {V _ { text {RMS}} ^ {2} over R}.}

Это уравнение можно использовать для любых периодических форма волны, например синусоидальный или же пилообразная форма волны, что позволяет нам рассчитать среднюю мощность, передаваемую на заданную нагрузку.

Вынимая квадратный корень из обоих этих уравнений и умножая их, получаем степень:

{ displaystyle P _ { text {Avg}} = V _ { text {RMS}} I _ { text {RMS}}.}

Оба значения зависят от пропорциональности напряжения и тока (т. Е. Нагрузка, р, является чисто резистивным). Реактивный нагрузки (то есть нагрузки, способные не только рассеивать энергию, но и накапливать ее) обсуждаются в теме Мощность переменного тока.

В общем случае переменный ток когда я(т) это синусоидальный тока, как это приблизительно верно для сетевого питания, среднеквадратичное значение легко вычислить из приведенного выше уравнения для непрерывного случая. Если я_п определяется как пиковый ток, тогда:

{ displaystyle I _ { text {RMS}} = { sqrt {{1 over {T_ {2} -T_ {1}}} int _ {T_ {1}} ^ {T_ {2}} left [I _ { text {p}} sin ( omega t) right] ^ {2} dt}},}

куда т время и ω это угловая частота (ω = 2 $π$ /Т, куда Т - период волны).

С я_п положительная константа:

{ displaystyle I _ { text {RMS}} = I _ { text {p}} { sqrt {{1 over {T_ {2} -T_ {1}}} { int _ {T_ {1}} ^ {T_ {2}} { sin ^ {2} ( omega t)} , dt}}}.}

Используя тригонометрическая идентичность чтобы исключить возведение триггерной функции в квадрат:

{ displaystyle { begin {align} I _ { text {RMS}} & = I _ { text {p}} { sqrt {{1 over {T_ {2} -T_ {1}}} { int _ {T_ {1}} ^ {T_ {2}} {1- cos (2 omega t) over 2} , dt}}} [3pt] & = I _ { text {p}} { sqrt {{1 over {T_ {2} -T_ {1}}} left [{t over 2} - { sin (2 omega t) over 4 omega} right] _ { Т_ {1}} ^ {Т_ {2}}}} конец {выровнено}}}

но поскольку интервал представляет собой целое число полных циклов (согласно определению RMS), члены sin будут сокращаться, оставляя:

{ displaystyle I _ { text {RMS}} = I _ { text {p}} { sqrt {{1 over {T_ {2} -T_ {1}}} left [{t over 2} справа] _ {T_ {1}} ^ {T_ {2}}}} = I _ { text {p}} { sqrt {{1 over {T_ {2} -T_ {1}}} {{T_ {2} -T_ {1}} over 2}}} = {I _ { text {p}} over { sqrt {2}}}.}

Подобный анализ приводит к аналогичному уравнению для синусоидального напряжения:

{ displaystyle V _ { text {RMS}} = {V _ { text {p}} over { sqrt {2}}},}

куда я_п представляет пиковый ток и V_п представляет пиковое напряжение.

Из-за их полезности при проведении расчетов мощности, перечисленные напряжения для розеток (например, 120 V в США, или 230 V в Европе) почти всегда указываются в значениях RMS, а не в пиковых значениях. Пиковые значения могут быть рассчитаны на основе значений RMS по приведенной выше формуле, которая подразумевает V_п = V_RMS × √2в предположении, что источником является чистая синусоида. Таким образом, пиковое значение сетевого напряжения в США составляет около 120 ×√2, или около 170 вольт. Размах напряжения, увеличенный вдвое, составляет около 340 вольт. Аналогичный расчет показывает, что пиковое напряжение сети в Европе составляет около 325 вольт, а максимальное напряжение сети - около 650 вольт.

Величины RMS, такие как электрический ток, обычно рассчитываются за один цикл. Однако для некоторых целей при расчете потерь мощности при передаче требуется среднеквадратичный ток за более длительный период. Применяется тот же принцип, и (например) ток 10 ампер, используемый в течение 12 часов каждый 24-часовой день, представляет средний ток 5 ампер, но среднеквадратичный ток 7,07 ампера в долгосрочной перспективе.

Период, термин Мощность RMS иногда ошибочно используется в аудиоиндустрии как синоним средняя мощность или же средняя мощность (он пропорционален квадрату среднеквадратичного напряжения или действующего тока в резистивной нагрузке). Для обсуждения измерений мощности звука и их недостатков см. Аудио мощность.

Скорость

в физика из газ молекулы, среднеквадратичная скорость определяется как квадратный корень из среднего квадрата скорости. Среднеквадратичная скорость идеального газа равна рассчитанный используя следующее уравнение:

{ displaystyle v _ { text {RMS}} = { sqrt {3RT over M}}}

куда р представляет газовая постоянная, 8,314 Дж / (моль · К), Т это температура газа в кельвины, и M это молярная масса газа в килограммах на моль. Общепринятая терминология для обозначения скорости по сравнению со скоростью состоит в том, что первая представляет собой скалярную величину последней. Следовательно, хотя средняя скорость находится между нулем и среднеквадратичной скоростью, средняя скорость для неподвижного газа равна нулю.

Ошибка

Когда два набора данных - например, один набор из теоретического прогноза, а другой из фактического измерения какой-либо физической переменной, например, - сравниваются, RMS парных разностей двух наборов данных может служить мерой того, насколько велика в среднем ошибка с 0. иметь в виду парных различий не измеряет изменчивость разницы, а изменчивость, как показано стандартное отклонение составляет около среднего, а не 0. Следовательно, среднеквадратичное значение различий является значимой мерой ошибки.

В частотной области

RMS можно вычислить в частотной области, используя Теорема Парсеваля. Для дискретизированного сигнала ${ Displaystyle х [п] = х (т = нТ)}$ , куда ${ displaystyle T}$ период выборки,

{ displaystyle sum _ {n = 1} ^ {N} {x ^ {2} [n]} = { frac {1} {N}} sum _ {m = 1} ^ {N} left | X [m] right | ^ {2},}

куда ${ displaystyle X [m] = OperatorName {FFT} {x [n] }}$ и N - размер выборки, то есть количество наблюдений в выборке и коэффициенты БПФ.

В этом случае RMS, вычисленное во временной области, такое же, как и в частотной области:

{ displaystyle { text {RMS}} {x [n] } = { sqrt {{ frac {1} {N}} sum _ {n} {x ^ {2} [n]}} } = { sqrt {{ frac {1} {N ^ {2}}} sum _ {m} {{ bigl |} X [m] { bigr |}} ^ {2}}} = { sqrt { sum _ {m} { left | { frac {X [m]} {N}} right | ^ {2}}}}.}

Связь с другой статистикой

Геометрический доказательство без слов который Максимум (а,б) > среднее квадратичное или же среднеквадратичное значение (QM) > среднее арифметическое (ЯВЛЯЮСЬ) > среднее геометрическое (GM) > гармоническое среднее (HM) > мин (а,б) двух положительных чисел а и б ^[7]

Если ${ displaystyle { bar {x}}}$ это среднее арифметическое и ${ displaystyle sigma _ {x}}$ это стандартное отклонение из численность населения или форма волны, тогда:^[8]

{ displaystyle x _ { text {rms}} ^ {2} = { overline {x}} ^ {2} + sigma _ {x} ^ {2} = { overline {x ^ {2}}} .}

Отсюда ясно, что среднеквадратичное значение всегда больше или равно среднему, поскольку среднеквадратичное значение также включает "ошибку" / квадратное отклонение.

Ученые-физики часто используют термин среднеквадратичное значение как синоним стандартное отклонение когда можно предположить, что входной сигнал имеет нулевое среднее значение, то есть относится к квадратному корню из среднего квадрата отклонения сигнала от заданной базовой линии или соответствия.^[9]^[10] Это полезно для инженеров-электриков при вычислении RMS сигнала "только переменный ток". Стандартное отклонение - это среднеквадратичное отклонение сигнала от среднего, а не около 0, Компонент постоянного тока удаляется (то есть RMS (сигнал) = stdev (сигнал), если средний сигнал равен 0).

Смотрите также

внешняя ссылка

[dicphys-1] а ^б Словарь по физике (6 изд.). Издательство Оксфордского университета. 2009 г. ISBN 9780199233991.

[2] Томпсон, Сильванус П. (1965). Расчет стал проще. Международное высшее образование Macmillan. п. 185. ISBN 9781349004874. Получено 5 июля 2020.

[3] Джонс, Алан Р. (2018). Вероятность, статистика и другие пугающие вещи. Рутледж. п. 48. ISBN 9781351661386. Получено 5 июля 2020.

[4] Картрайт, Кеннет V (осень 2007 г.). «Определение эффективного или среднеквадратичного напряжения различных форм волны без расчетов» (PDF). Технологический интерфейс. 8 (1): 20 с.

[5] Нэстасе, Адриан С. «Как получить среднеквадратичное значение импульсных и прямоугольных сигналов». MasteringElectronicsDesign.com. Получено 21 января 2015.

[6] «Сделайте более точные измерения СКЗ переменного тока с помощью цифрового мультиметра» (PDF). Keysight. Keysight. Получено 15 января 2019.

[7] Если AC = а и BC = б. OC = ЯВЛЯЮСЬ из а и б, и радиус р = QO = OG.
С помощью Теорема Пифагора, QC² = QO² + OC² ∴ QC = √QO² + OC² = QM.
Используя теорему Пифагора, OC² = OG² + GC² ∴ GC = √OC² - OG² = GM.
С помощью похожие треугольники, HC/GC = GC/OC ∴ HC = GC²/OC = HM.

[8] Крис С. Биссел; Дэвид А. Чепмен (1992). Передача цифрового сигнала (2-е изд.). Издательство Кембриджского университета. п. 64. ISBN 978-0-521-42557-5.

[9] Вайсштейн, Эрик В. "Среднеквадратичный". MathWorld.

[10] "ROOT, TH1: GetRMS".

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

Navigation