WikiDer > Межфазное термическое сопротивление
В ведущий раздел этой статьи может потребоваться переписать. (Декабрь 2019 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
Межфазное термическое сопротивление, также известный как тепловое граничное сопротивление, или же Капице сопротивление, является мерой сопротивления интерфейса тепловому потоку. Это термическое сопротивление отличается от Контактное сопротивление (не путать с сопротивление электрического контакта), потому что он существует даже на атомарно совершенных интерфейсах. Из-за различий в электронных и колебательных свойствах различных материалов, когда носитель энергии (фонон или электрон, в зависимости от материала) пытается пересечь границу раздела, он будет рассеиваться на границе раздела. Вероятность передачи после рассеяния будет зависеть от доступных энергетических состояний на стороне 1 и стороне 2 интерфейса.
Если предположить, что к границе раздела приложен постоянный тепловой поток, это межфазное тепловое сопротивление приведет к конечному скачку температуры на границе раздела. Из расширения Закон Фурье, мы можем написать
куда применяемый флюс, - наблюдаемое падение температуры, - тепловое граничное сопротивление, а - его обратная или тепловая граничная проводимость.
Понимание термического сопротивления на границе раздела двух материалов имеет первостепенное значение при изучении его термических свойств. Интерфейсы часто вносят значительный вклад в наблюдаемые свойства материалов. Это еще более важно для наноразмер системы, в которых границы раздела могут существенно повлиять на свойства по отношению к объемным материалам.[1]
Низкое тепловое сопротивление на границах раздела технологически важно для приложений, где требуется очень высокое тепловыделение. Это вызывает особую озабоченность при разработке микроэлектронных полупроводниковых устройств, как это определено в Международной дорожной карте технологий для полупроводников в 2004 г., где предполагается, что устройство размером 8 нм будет генерировать до 100000 Вт / см.2 и потребуется эффективное рассеивание тепла ожидаемого теплового потока на уровне кристалла 1000 Вт / см2 что на порядок выше, чем у нынешних устройств.[2] С другой стороны, приложения, требующие хорошей теплоизоляции, такие как турбины реактивных двигателей, выиграют от интерфейсов с высоким тепловым сопротивлением. Для этого также потребуются поверхности раздела материалов, устойчивые при очень высокой температуре. Примерами являются металлокерамические композиты, которые в настоящее время используются для этих приложений. Высокого термического сопротивления можно достичь и с помощью многослойных систем.
Как указано выше, тепловое граничное сопротивление возникает из-за рассеяния носителей заряда на границе раздела. Тип разбросанного носителя будет зависеть от материалов, из которых изготовлены интерфейсы. Например, на границе раздела металл-металл эффекты рассеяния электронов будут преобладать над тепловым сопротивлением границы, поскольку электроны являются основными носителями тепловой энергии в металлах.
Две широко используемые модели прогнозирования - это модель акустического рассогласования (AMM) и модель диффузного рассогласования (DMM). AMM предполагает геометрически совершенный интерфейс, а перенос фононов через него является полностью упругим, рассматривая фононы как волны в континууме. С другой стороны, цифровой мультиметр предполагает, что рассеяние на границе раздела является диффузным, что верно для границ раздела с характерной шероховатостью при повышенных температурах.
Молекулярная динамика (МД) моделирование - мощный инструмент для исследования межфазного термического сопротивления. Недавние исследования методом МД продемонстрировали, что межфазное термическое сопротивление твердое тело-жидкость снижается на наноструктурированных твердых поверхностях за счет увеличения энергии взаимодействия твердое тело-жидкость на единицу площади и уменьшения разницы в колебательных характеристиках. плотность состояний между твердым телом и жидкостью.[3]
Теоретические модели
Есть две основные модели, которые используются для понимания теплового сопротивления интерфейсов: модели акустического несоответствия и диффузного несоответствия (AMM и DMM соответственно). Обе модели основаны только на переносе фононов без учета электрических вкладов. Таким образом, он должен применяться к интерфейсам, в которых хотя бы один из материалов является электроизоляционным. Для обеих моделей предполагается, что интерфейс ведет себя точно так же, как объем по обе стороны от границы (например, объемные дисперсии фононов, скорости и т. Д.). Тепловое сопротивление возникает в результате переноса фононов через интерфейс. Энергия передается, когда фононы с более высокой энергией, которые существуют в более высокой плотности в более горячем материале, распространяются к более холодным материалам, которые, в свою очередь, передают фононы с более низкой энергией, создавая сетку поток энергии.[4]
Решающим фактором в определении теплового сопротивления на границе раздела является перекрытие фононных состояний. Учитывая два материала, A и B, если материал A имеет низкую заселенность (или не имеет заселенности) фононов с определенным значением k, фононов будет очень мало. волновой вектор распространяться от А к Б. Далее, из-за подробный баланс, очень немногие фононы этого волнового вектора будут распространяться в противоположном направлении, от B к A, даже если материал B имеет большую популяцию фононов с этим волновым вектором. Таким образом, поскольку перекрытие между фононными дисперсиями невелико, существует меньше режимов, обеспечивающих передачу тепла в материале, что дает высокое термическое межфазное сопротивление по сравнению с материалами с высокой степенью перекрытия.[5]И AMM, и DMM отражают этот принцип, но различаются условиями, которые они требуют для распространения через интерфейс. Ни одна из моделей не является универсально эффективной для прогнозирования сопротивления термического интерфейса (за исключением очень низкой температуры), но для большинства материалов они действуют как верхний и нижний пределы реального поведения.
Обе модели сильно различаются в трактовке рассеяния на границе раздела. В AMM интерфейс считается идеальным, что не приводит к рассеянию, поэтому фононы упруго распространяются через интерфейс. Волновые векторы, которые распространяются через границу раздела, определяются законом сохранения импульса. В DMM предполагается противоположная крайность - идеально рассеивающая поверхность раздела. В этом случае волновые векторы, которые распространяются через поверхность раздела, являются случайными и не зависят от фононов, падающих на поверхность раздела. Для обеих моделей необходимо соблюдать точный баланс.
Для обеих моделей применимы некоторые основные уравнения. Поток энергии от одного материала к другому равен:
где n - количество фононов в заданном волновом векторе и импульс, E - энергия, а α - вероятность передачи через интерфейс. Таким образом, чистый поток представляет собой разность потоков энергии:
Поскольку оба потока зависят от T1 и т2, соотношение между потоком и разностью температур можно использовать для определения сопротивления термического интерфейса на основе:
где A - площадь интерфейса. Эти основные уравнения составляют основу обеих моделей. n определяется на основе Дебая модель и Статистика Бозе – Эйнштейна. Энергия дается просто:
где ν - скорость звука в материале. Основное различие между двумя моделями - это вероятность передачи, определение которого более сложно. В каждом случае это определяется базовыми допущениями, которые формируют соответствующие модели. Предположение об упругом рассеянии затрудняет передачу фононов через границу раздела, что приводит к снижению вероятности. В результате модель акустического рассогласования обычно представляет собой верхний предел сопротивления теплового интерфейса, тогда как модель диффузного рассогласования представляет собой нижний предел.[6]
Примеры
Интерфейсы жидкого гелия
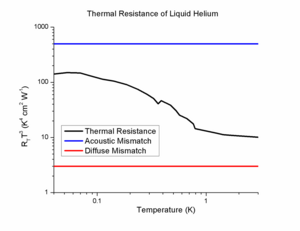
Наличие теплового сопротивления интерфейса, соответствующего скачкообразной температуре на границе раздела, было впервые предложено на основе исследований жидкий гелий в 1936 году. Хотя эта идея была впервые предложена в 1936 году,[5] только в 1941 году, когда Петр Капица (Петр Капица) провел первое систематическое исследование поведения теплового интерфейса в жидком гелии.[7] Первая крупная модель для теплопередача на границах раздела была модель акустического рассогласования, которая предсказывала T−3 зависимость температуры от межфазного сопротивления, но это не смогло должным образом смоделировать теплопроводность границ раздела гелия на целых два порядка величины. Еще одно удивительное поведение термического сопротивления наблюдалось в давление зависимость. Поскольку скорость звука в жидком гелии сильно зависит от температуры, модель акустического несоответствия предсказывает сильную зависимость межфазного сопротивления от давления. Исследования 1960 года неожиданно показали, что межфазное сопротивление почти не зависит от давления, что предполагает доминирование других механизмов.
Теория акустического рассогласования предсказала очень высокое тепловое сопротивление (низкую теплопроводность) на границах раздела твердое тело-гелий. Это было потенциально катастрофой для исследователей, работающих при сверхнизких температурах, потому что это сильно замедляет скорость охлаждения при низких температурах. К счастью, такого большого термического сопротивления не наблюдалось из-за множества механизмов, способствующих переносу фононов. В жидком гелии Силы Ван-дер-Ваальса фактически работают для отверждения первых нескольких монослоев относительно твердого тела. Этот пограничный слой очень похож на антибликовое покрытие в оптике, так что фононы, которые обычно отражаются от интерфейса, фактически передаются через интерфейс. Это также помогает понять независимость теплопроводности от давления. Последний доминирующий механизм аномально низкого теплового сопротивления границ раздела жидкого гелия - это влияние шероховатость поверхности, что не учитывается в модели акустического рассогласования. Более подробную теоретическую модель этого аспекта см. В статье A. Khater и J. Szeftel.[8] Нравиться электромагнитные волны которые производят поверхностные плазмоны на шероховатых поверхностях фононы также могут вызывать поверхностные волны. Когда эти волны в конечном итоге рассеиваются, они обеспечивают другой механизм передачи тепла через границу раздела. Точно так же фононы также способны производить мимолетные волны в полное внутреннее отражение геометрия. В результате, когда эти волны рассеиваются в твердом теле, от гелия передается дополнительное тепло сверх того, что предсказывает теория акустического рассогласования. Более полный обзор по этой теме см. В обзоре Swartz.[9]
Отличная теплопроводность при комнатной температуре
В целом в материалах есть два типа теплоносителей: фононы и электроны. Свободный электронный газ, содержащийся в металлах, является очень хорошим проводником тепла и доминирует теплопроводность. Тем не менее, все материалы демонстрируют передачу тепла за счет переноса фононов, поэтому тепло течет даже в диэлектрических материалах, таких как кремнезем. Межфазная теплопроводность - это мера того, насколько эффективно теплоносители переходят от одного материала к другому. Самое низкое на сегодняшний день измерение теплопроводности при комнатной температуре - это прибор с концевым выводом из Bi / водорода. алмаз с теплопроводностью 8,5 МВт · м−2 K−1. Как металл, висмут содержит много электронов, которые служат первичными теплоносителями. С другой стороны, алмаз является очень хорошим электрическим изолятором (хотя он имеет очень высокую теплопроводность), поэтому перенос электронов между материалами равен нулю. Кроме того, эти материалы имеют очень разные параметры решетки, поэтому фононы не могут эффективно взаимодействовать через интерфейс. Наконец, Температура Дебая Между материалами существенно отличается. В результате висмут, имеющий низкую температуру Дебая, имеет много фононов на низких частотах. С другой стороны, у алмаза очень высокая температура Дебая, и большинство его теплоносящих фононов находятся на частотах намного выше, чем присутствующие в висмуте.[10]
Увеличивая теплопроводность, большинство опосредованных фононами интерфейсов (диэлектрик-диэлектрик и металл-диэлектрик) имеют теплопроводность от 80 до 300 МВт · м.−2 K−1. Наибольшая измеренная на сегодняшний день теплопроводность, опосредованная фононами, находится между TiN (нитрид титана) и MgO. Эти системы очень похожи решетчатые конструкции и температуры Дебая. В то время как нет свободных электронов для увеличения теплопроводности границы раздела, аналогичные физические свойства двух кристаллов способствуют очень эффективной передаче фононов между двумя материалами.[7]
В самом верхнем конце спектра один из самых высоких значений теплопроводности. измеренный между алюминий и медь. При комнатной температуре интерфейс Al-Cu имеет проводимость 4 ГВт · м.−2 K−1. Высокая теплопроводность интерфейса не должна быть неожиданной, учитывая высокую электропроводность обоих материалов.[11]
Межфазное сопротивление в углеродных нанотрубках
Превосходная теплопроводность углеродных нанотрубок делает их отличным кандидатом для создания композитных материалов. Но межфазное сопротивление влияет на эффективную теплопроводность. Эта область недостаточно изучена, и было проведено всего несколько исследований, чтобы понять основной механизм этого сопротивления.[12][13]
Рекомендации
- ^ Ли, человек; Кан, Джун; Нгуен, Хуу; Ву, Хуан; Ху, Юнцзе (2019). «Сопротивление анизотропной тепловой границы через двумерный черный фосфор: эксперимент и атомистическое моделирование межфазного переноса энергии». Современные материалы. 31 (33): 1901021. Дои:10.1002 / adma.201901021.
- ^ Ху, Мин; Кеблински, Павел; Ван, Цзянь-Шэн; Раравикар, Начикет (2008). «Межфазная теплопроводность кремния и вертикальной углеродной нанотрубки». Журнал прикладной физики. 104 (8): 083503. Bibcode:2008JAP ... 104х3503Н. Дои:10.1063/1.3000441.
- ^ Ху, Хань; Солнце, Ин (2012). «Влияние наноструктур на сопротивление Капице на границе раздела вода-золото во время кипения: исследование молекулярной динамики». Журнал прикладной физики. Издательство AIP. 112 (5): 053508–053508–6. Bibcode:2012JAP ... 112e3508H. Дои:10.1063/1.4749393. ISSN 0021-8979.
- ^ Шварц, E.T. Граничное сопротивление твердого тела и твердого тела, докторская диссертация, Корнельский университет, 1987 г.
- ^ а б c Swartz, E.T .; Поль, Р. О. (1989-07-01). «Термическое граничное сопротивление». Обзоры современной физики. Американское физическое общество (APS). 61 (3): 605–668. Bibcode:1989РвМП ... 61..605С. Дои:10.1103 / revmodphys.61.605. ISSN 0034-6861.
- ^ Цзэн Т. и Чен Г., Транзакции ASME, 123, (2001).
- ^ а б Капица П.Л. // Журн. Физ. (СССР) 4 (1941).
- ^ Хатер, А .; Szeftel, J. (1987-05-01). «Теория сопротивления Капице». Физический обзор B. Американское физическое общество (APS). 35 (13): 6749–6755. Bibcode:1987PhRvB..35.6749K. Дои:10.1103 / Physrevb.35.6749. ISSN 0163-1829. PMID 9940924.
- ^ а б Лео, Хо-Ки; Кэхилл, Дэвид Г. (2006-04-03). «Теплопроводность границ раздела между сильно разнородными материалами». Физический обзор B. Американское физическое общество (APS). 73 (14): 144301. Bibcode:2006ПхРвБ..73н4301Л. Дои:10.1103 / Physrevb.73.144301. ISSN 1098-0121.
- ^ а б Costescu, Ruxandra M .; Wall, Marcel A .; Кэхилл, Дэвид Г. (27 февраля 2003 г.). «Теплопроводность эпитаксиальных интерфейсов». Физический обзор B. Американское физическое общество (APS). 67 (5): 054302. Bibcode:2003PhRvB..67e4302C. Дои:10.1103 / Physrevb.67.054302. ISSN 0163-1829.
- ^ а б Gundrum, Bryan C .; Кэхилл, Дэвид Дж .; Авербак, Роберт С. (30 декабря 2005 г.). «Теплопроводность границ раздела металл-металл». Физический обзор B. Американское физическое общество (APS). 72 (24): 245426. Bibcode:2005PhRvB..72x5426G. Дои:10.1103 / Physrevb.72.245426. ISSN 1098-0121.
- ^ Чжун, Хунлян; Льюкс, Дженнифер Р. (01.09.2006). «Межфазное термическое сопротивление между углеродными нанотрубками: моделирование молекулярной динамики и аналитическое тепловое моделирование». Физический обзор B. Американское физическое общество (APS). 74 (12): 125403. Bibcode:2006PhRvB..74l5403Z. Дои:10.1103 / Physrevb.74.125403. ISSN 1098-0121.
- ^ Эстрада, Дэвид; Поп, Эрик (14.02.2011). "Рассеяние изображений и горячие точки в транзисторах сети углеродных нанотрубок". Письма по прикладной физике. Издательство AIP. 98 (7): 073102. arXiv:1011.4551. Bibcode:2011АпФЛ..98г3102Э. Дои:10.1063/1.3549297. ISSN 0003-6951. S2CID 40975236.









