WikiDer > Линейная функция (исчисление)

Эта статья отсутствует информация о многомерных и векторнозначных функциях, которые необходимо учитывать, поскольку эта статья связана с Матрица якобиана. Разверните статью, чтобы включить эту информацию. Дополнительные сведения могут быть указаны на страница обсуждения. (Февраль 2020 г.)

График линейной функции: ${ Displaystyle у (х) = - х + 2}$

В исчисление и смежных областях математики, линейная функция от действительных чисел к действительным числам представляет собой функцию, график которой (в Декартовы координаты) это линия в плоскости.^[1] Характерным свойством линейных функций является то, что при изменении входной переменной изменение выходной пропорциональный к изменению входа.

Линейные функции связаны с линейные уравнения.

Характеристики

Линейная функция - это полиномиальная функция в которой Переменная Икс имеет степень не более одного:^[2]

${ displaystyle f (x) = ax + b}$.

Такая функция называется линейный потому что это график, множество всех точек ${ Displaystyle (х, е (х))}$ в Декартова плоскость, это линия. Коэффициент а называется склон функции и линии (см. ниже).

Если наклон ${ displaystyle a = 0}$, это постоянная функция ${ displaystyle f (x) = b}$ определяя горизонтальную линию, которую некоторые авторы исключают из класса линейных функций.^[3] С этим определением степень линейного многочлена будет ровно один, а его график будет линией, которая не является ни вертикальной, ни горизонтальной. Однако в этой статье ${ displaystyle a neq 0}$ требуется, поэтому постоянные функции будут считаться линейными.

Если ${ displaystyle b = 0}$ то линейная функция называется однородный. Такая функция определяет линию, проходящую через начало системы координат, то есть точку ${ Displaystyle (х, у) = (0,0)}$. В текстах по продвинутой математике термин линейная функция часто обозначает специфически однородные линейные функции, а термин аффинная функция используется для общего случая, который включает ${ displaystyle b neq 0}$.

Естественный домен линейной функции ${ displaystyle f (x)}$, набор разрешенных входных значений для Икс, это весь набор действительные числа, ${ Displaystyle х in mathbb {R}.}$ Такие функции также можно рассматривать с Икс в произвольном поле, принимая коэффициенты а, б в этой области.

График ${ displaystyle y = f (x) = ax + b}$ не вертикальная линия, имеющая ровно одно пересечение с уось, ее у-точка перехвата ${ displaystyle (x, y) = (0, b).}$ В у-перехват значения ${ displaystyle y = f (0) = b}$ также называется Первоначальный значение из ${ displaystyle f (x).}$ Если ${ displaystyle a neq 0,}$ график представляет собой негоризонтальную линию, имеющую ровно одно пересечение с Иксось, Икс-точка перехвата ${ displaystyle (x, y) = (- { tfrac {b} {a}}, 0).}$ В Икс-перехват значения ${ displaystyle x = - { tfrac {b} {a}},}$ решение уравнения ${ displaystyle f (x) = 0,}$ также называется корень или же нуль из ${ displaystyle f (x).}$

Склон

Наклон линии - это отношение ${ Displaystyle { tfrac { Delta y} { Delta x}}}$ между изменением Икс, обозначенный ${ displaystyle Delta x}$, и соответствующее изменение у, обозначенный ${ displaystyle Delta y}$

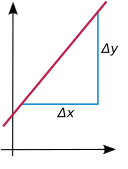
В склон длины невертикальной линии - это число, которое измеряет, насколько крутой наклон линия (подъем-выход). Если линия - это график линейной функции ${ displaystyle f (x) = ax + b}$, этот наклон задается постоянной а.

Наклон измеряет постоянную скорость изменения ${ displaystyle f (x)}$ на единицу изменения в Икс: всякий раз, когда ввод Икс увеличивается на единицу, выход изменяется на а единицы: ${ Displaystyle е (х {+} 1) = е (х) + а}$, и в более общем плане ${ displaystyle f (x {+} Delta x) = f (x) + a Delta x}$ на любой номер ${ displaystyle Delta x}$. Если наклон положительный, ${ displaystyle a> 0}$, то функция ${ displaystyle f (x)}$ растет; если ${ displaystyle a <0}$, тогда ${ displaystyle f (x)}$ уменьшается

В исчисление, производная общей функции измеряет скорость ее изменения. Линейная функция ${ displaystyle f (x) = ax + b}$ имеет постоянную скорость изменения, равную его крутизне а, поэтому его производная - постоянная функция ${ Displaystyle е , '(х) = а}$.

Основная идея дифференциального исчисления состоит в том, что любое гладкий функция ${ displaystyle f (x)}$ (не обязательно линейный) может быть близко приблизительный рядом с заданной точкой ${ displaystyle x = c}$ единственной линейной функцией. В производная ${ displaystyle f , '(c)}$ - наклон этой линейной функции, и приближение: ${ Displaystyle е (х) приблизительно е , '(с) (х {-} с) + е (с)}$ за ${ Displaystyle х приблизительно с}$. График линейной аппроксимации - это касательная линия графика ${ Displaystyle у = е (х)}$ в момент ${ Displaystyle (с, е (с))}$. Наклон производной ${ displaystyle f , '(c)}$ обычно меняется в зависимости от точки c. Линейные функции можно охарактеризовать как единственные действительные функции, производная которых постоянна: если ${ Displaystyle е , '(х) = а}$ для всех Икс, тогда ${ displaystyle f (x) = ax + b}$ за ${ displaystyle b = f (0)}$.

Уклон-пересечение, точечный уклон и двухточечные формы

Заданная линейная функция ${ displaystyle f (x)}$ можно записать в несколько стандартных формул, отображающих его различные свойства. Самый простой - это форма пересечения склонов:

${ displaystyle f (x) = ax + b}$,

откуда сразу виден откос а и начальное значение ${ displaystyle f (0) = b}$, какой у-перехват графика ${ Displaystyle у = е (х)}$.

Учитывая наклон а и одно известное значение ${ displaystyle f (x_ {0}) = y_ {0}}$, мы пишем точечно-наклонная форма:

${ displaystyle f (x) = a (x {-} x_ {0}) + y_ {0}}$.

Графически это дает линию ${ Displaystyle у = е (х)}$ с уклоном а проходя через точку ${ displaystyle (x_ {0}, y_ {0})}$.

В двухточечная форма начинается с двух известных значений ${ displaystyle f (x_ {0}) = y_ {0}}$ и ${ displaystyle f (x_ {1}) = y_ {1}}$. Один вычисляет наклон ${ displaystyle a = { tfrac {y_ {1} -y_ {0}} {x_ {1} -x_ {0}}}}$ и вставляет это в форму точки наклона:

${ displaystyle f (x) = { tfrac {y_ {1} -y_ {0}} {x_ {1} -x_ {0}}} (x {-} x_ {0} !) + y_ {0 }}$.

Его график ${ Displaystyle у = е (х)}$ единственная прямая, проходящая через точки ${ displaystyle (x_ {0}, y_ {0} !), (x_ {1}, y_ {1} !)}$. Уравнение ${ Displaystyle у = е (х)}$ также можно написать, чтобы подчеркнуть постоянный наклон:

${ displaystyle { frac {y-y_ {0}} {x-x_ {0}}} = { frac {y_ {1} -y_ {0}} {x_ {1} -x_ {0}}} }$.

Связь с линейными уравнениями

Линейные функции обычно возникают из практических задач, связанных с переменными. ${ displaystyle x, y}$ с линейной зависимостью, то есть подчиняясь линейное уравнение ${ displaystyle Ax + By = C}$. Если ${ displaystyle B neq 0}$, можно решить это уравнение относительно у, получение

${ displaystyle y = - { tfrac {A} {B}} x + { tfrac {C} {B}} = ax + b,}$

где мы обозначаем ${ displaystyle a = - { tfrac {A} {B}}}$ и ${ displaystyle b = { tfrac {C} {B}}}$. То есть можно считать у как зависимая переменная (выход), полученная из независимой переменной (вход) Икс через линейную функцию: ${ displaystyle y = f (x) = ax + b}$. в ху-координатная плоскость, возможные значения ${ Displaystyle (х, у)}$ образуют линию, график функции ${ displaystyle f (x)}$. Если ${ displaystyle B = 0}$ в исходном уравнении результирующая строка ${ Displaystyle х = { tfrac {C} {A}}}$ вертикально и не может быть записано как ${ Displaystyle у = е (х)}$.

Особенности графика ${ displaystyle y = f (x) = ax + b}$ можно интерпретировать в терминах переменных Икс и у. В у-intercept - начальное значение ${ displaystyle y = f (0) = b}$ в ${ displaystyle x = 0}$. Склон а измеряет скорость изменения выхода у на единицу изменения на входе Икс. На графике перемещение на одну единицу вправо (увеличение Икс на 1) перемещает у-ценность на а: то есть, ${ Displaystyle е (х {+} 1) = е (х) + а}$. Отрицательный наклон а указывает на уменьшение у за каждое увеличение Икс.

Например, линейная функция ${ displaystyle y = -2x + 4}$ имеет наклон ${ displaystyle a = -2}$, у-точка перехвата ${ displaystyle (0, b) = (0,4)}$, и Икс-точка перехвата ${ displaystyle (2,0)}$.

Пример

Предположим, салями и колбаса стоят 6 и 3 евро за килограмм, а мы хотим купить на сумму 12 евро. Сколько каждого из них мы можем купить? Если Икс килограммы салями и у килограмм колбасы стоит 12 евро, тогда 6 евро * x + 3 евро * y = 12 евро. Решение для у дает форму точечного уклона ${ displaystyle y = -2x + 4}$, как указано выше. То есть, если сначала выбрать количество салями Иксколичество колбасы можно вычислить как функцию ${ Displaystyle у = е (х) = - 2x + 4}$. Поскольку салями стоит вдвое дороже колбасы, добавление одного килограмма салями уменьшает колбасу на 2 килограмма: ${ displaystyle f (x {+} 1) = f (x) -2}$, а наклон равен −2. В у-точка перехвата ${ Displaystyle (х, у) = (0,4)}$ соответствует покупке всего 4 кг колбасы; в то время как Икс-точка перехвата ${ Displaystyle (х, у) = (2,0)}$ соответствует покупке всего 2 кг салями.

Обратите внимание, что на графике есть точки с отрицательными значениями Икс или же у, которые не имеют значения с точки зрения исходных переменных (если только мы не представляем себе продажу мяса мяснику). Таким образом, мы должны ограничить нашу функцию ${ displaystyle f (x)}$ в домен ${ Displaystyle 0 Leq х Leq 2}$.

Также мы могли выбрать у в качестве независимой переменной и вычислить Икс посредством обратный линейная функция: ${ Displaystyle х = г (у) = - { tfrac {1} {2}} у + 2}$ по домену ${ Displaystyle 0 Leq Y Leq 4}$.

Связь с другими классами функций

Если коэффициент переменной не равен нулю (а ≠ 0), то линейная функция представлена степень 1 многочлен (также называемый линейный полином), иначе это постоянная функция - тоже полиномиальная функция, но нулевой степени.

Прямая линия, нарисованная в другой системе координат, может представлять другие функции.

Например, он может представлять экспоненциальная функция когда это значения выражаются в логарифмическая шкала. Это означает, что когда бревно(грамм(Икс)) является линейной функцией Икс, функция грамм экспоненциально. В линейных функциях увеличение ввода на одну единицу приводит к увеличению вывода на фиксированную величину, которая представляет собой наклон графика функции. В случае экспоненциальных функций увеличение ввода на одну единицу приводит к увеличению вывода на фиксированное кратное число, которое известно как основание экспоненциальной функции.

Если обе аргументы а значения функции указаны в логарифмическом масштабе (т.е. когда бревно(у) является линейной функцией бревно(Икс)), то прямая линия представляет собой сила закона:

${ displaystyle log _ {r} y = a log _ {r} x + b quad Rightarrow quad y = r ^ {b} cdot x ^ {a}}$

Архимедова спираль, определяемая полярным уравнением r =¹⁄₂θ + 2

С другой стороны, график линейной функции через полярные координаты:

${ Displaystyle г = е ( тета) = а тета + Ь}$

является Архимедова спираль если ${ displaystyle a neq 0}$ и круг иначе.

Примечания

Смотрите также

• Аффинная карта, обобщение
• Арифметическая прогрессия, линейная функция целочисленного аргумента

Рекомендации

• Джеймс Стюарт (2012), Исчисление: ранние трансцендентальные теории, издание 7E, Brooks / Cole. ISBN 978-0-538-49790-9
• Своковски, Эрл В. (1983), Исчисление с аналитической геометрией (Альтернативный редактор), Бостон: Prindle, Weber & Schmidt, ISBN 0871503417

внешняя ссылка

• https://web.archive.org/web/20130524101825/http://www.math.okstate.edu/~noell/ebsm/linear.html
• http://www.corestandards.org/assets/CCSSI_Math%20Standards.pdf