WikiDer > Вычисление медицинских изображений
Вычисление медицинских изображений (MIC) является междисциплинарной областью на пересечении Информатика, информационная инженерия, электротехника, физика, математика и лекарство. В этой области разрабатываются вычислительные и математические методы для решения задач, относящихся к медицинским изображениям, и их использования для биомедицинских исследований и клинической помощи.
Основная цель MIC - извлечь клинически значимую информацию или знания из медицинских изображений. Хотя он тесно связан с областью медицинская визуализация, MIC фокусируется на вычислительном анализе изображений, а не на их получении. Методы можно сгруппировать в несколько больших категорий: сегментация изображения, регистрация изображения, физиологическое моделирование на основе изображений, и другие.
Формы данных
Вычисление медицинских изображений обычно работает с однородно дискретизированными данными с регулярным пространственным интервалом x-y-z (изображения в 2D и объемы в 3D, обычно называемые изображениями). В каждой точке выборки данные обычно представлены в интеграл форма, такая как знаковая и беззнаковая короткая (16-битная), хотя формы от беззнаковой char (8-битной) до 32-битной с плавающей запятой не редкость. Конкретное значение данных в точке выборки зависит от модальности: например, КТ получение собирает значения радиоплотности, а Получение МРТ может собрать Т1 или же Т2взвешенные изображения. Продольные, изменяющиеся во времени захваты могут получать или не получать изображения с регулярными временными шагами. Фанатичные изображения благодаря таким модальностям, как УЗИ с изогнутой решеткой также распространены и требуют для обработки различных репрезентативных и алгоритмических методов. Другие формы данных включают обрезанные изображения из-за наклон портала во время приобретения; и неструктурированные сетки, такие как гексаэдрические и тетраэдрические формы, которые используются в продвинутых биомеханический анализ (например, деформация тканей, перенос сосудов, костные имплантаты).
Сегментация
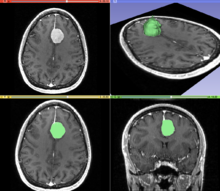
Сегментация - это процесс разделения изображения на разные значимые сегменты. В медицинской визуализации эти сегменты часто соответствуют различным классам тканей, органы, патологии или другие биологически значимые структуры.[1] Сегментация медицинских изображений затруднена из-за низкой контрастности, шума и других неоднозначностей изображения. Хотя есть много методы компьютерного зрения для сегментации изображенийнекоторые из них были адаптированы специально для обработки медицинских изображений. Ниже приведены примеры методов в этой области; реализация основана на опыте, который могут предоставить врачи.
- Сегментация на основе атласа: Для многих приложений клинический эксперт может вручную пометить несколько изображений; сегментирование невидимых изображений - это вопрос экстраполяции этих вручную помеченных обучающих изображений. Методы этого стиля обычно называют методами сегментации на основе атласа. Методы параметрического атласа обычно объединяют эти обучающие изображения в одно изображение атласа,[2] в то время как непараметрические методы атласа обычно используют все обучающие изображения по отдельности.[3] Методы на основе атласа обычно требуют использования регистрация изображения для выравнивания изображения или изображений атласа с новым, невидимым изображением.
- Сегментация на основе формы: Многие методы параметризуют форму шаблона для данной конструкции, часто полагаясь на контрольные точки вдоль границы. Затем вся форма деформируется, чтобы соответствовать новому изображению. Двумя наиболее распространенными техниками на основе форм являются модели активных форм. [4] и модели активного внешнего вида.[5] Эти методы оказали большое влияние и привели к созданию аналогичных моделей.[6]
- Сегментация на основе изображений: Некоторые методы инициируют шаблон и уточняют его форму в соответствии с данными изображения, сводя к минимуму меры интегральной ошибки, например Модель активного контура и его вариации.[7]
- Интерактивная сегментация: Интерактивные методы полезны, когда врачи могут предоставить некоторую информацию, такую как область семени или приблизительный контур области для сегментации. Затем алгоритм может многократно уточнять такую сегментацию под руководством врача или без него. Ручная сегментация с использованием таких инструментов, как кисть для явного определения класса ткани каждого пикселя, остается золотым стандартом для многих приложений для обработки изображений. Недавно принципы обратной связи теория управления были включены в сегментацию, что дает пользователю большую гибкость и позволяет автоматически исправлять ошибки.[8]
- Субъективная поверхностная сегментация: Этот метод основан на идее эволюции функции сегментации, которая регулируется моделью адвекции-диффузии.[9] Чтобы сегментировать объект, требуется начальное значение сегментации (это начальная точка, которая определяет приблизительное положение объекта на изображении). Следовательно, строится начальная функция сегментации. Идея метода субъективной поверхности [10][11][12] заключается в том, что положение начального числа является основным фактором, определяющим форму этой функции сегментации.
Однако существует и другая классификация методов сегментации изображений, аналогичная вышеперечисленным категориям. Более того, мы можем классифицировать другую группу как «Гибридную», основанную на сочетании методов.[13]
Постановка на учет
Регистрация изображения это процесс, который ищет правильное выравнивание изображений.[14][15][16][17] В простейшем случае выравниваются два изображения. Обычно одно изображение обрабатывается как целевое изображение, а другое - как исходное; исходное изображение преобразуется, чтобы соответствовать целевому изображению. В процедура оптимизации обновляет преобразование исходного изображения на основе значения подобия, которое оценивает текущее качество совмещения. Эта итерационная процедура повторяется до тех пор, пока не будет найден (локальный) оптимум. Примером может служить регистрация КТ и ДОМАШНИЙ ПИТОМЕЦ изображения для объединения структурной и метаболической информации (см. рисунок).
Регистрация изображений используется в различных медицинских приложениях:
- Изучение временных изменений. Продольные исследования получать изображения за несколько месяцев или лет для изучения долгосрочных процессов, таких как прогрессирование заболевания. Временные ряды соответствуют изображениям, полученным в течение одного сеанса (секунды или минуты). Их можно использовать для изучения когнитивных процессов, деформаций сердца и дыхания.
- Объединение дополнительной информации из разных методы визуализации. Примером может служить сочетание анатомической и функциональной информации. Поскольку размер и форма структур различаются в зависимости от модальности, оценить качество совмещения сложнее. Это привело к использованию меры сходства Такие как взаимная информация.[18]
- Характеристика совокупности субъектов. В отличие от внутрисубъектной регистрации, взаимно однозначное сопоставление между субъектами может не существовать, в зависимости от структурной изменчивости интересующего органа. Для построения атласа в г. вычислительная анатомия.[19] Здесь цель состоит в том, чтобы статистически смоделировать анатомию органов у разных субъектов.
- Компьютерная хирургия. В компьютерной хирургии предоперационные изображения, такие как компьютерная томография или магнитно-резонансная томография, регистрируются в интраоперационных изображениях или системах отслеживания для облегчения управления изображением или навигации.
При регистрации изображения следует учитывать несколько важных моментов:
- В модель трансформации. Обычный выбор жесткий, аффинный, и деформируемый модели трансформации. B-шлиц и шлиц тонкой пластины модели обычно используются для параметризованных полей преобразования. Непараметрические или плотные поля деформации несут вектор смещения в каждом месте сетки; это требует дополнительных регуляризация ограничения. Специфическим классом полей деформации являются диффеоморфизмы, являющиеся обратимыми преобразованиями с гладким обратным.
- Метрика подобия. Функция расстояния или сходства используется для количественной оценки качества регистрации. Это сходство можно вычислить либо по исходным изображениям, либо по признакам, извлеченным из изображений. Общие меры сходства - это сумма квадратов расстояний (SSD), коэффициент корреляции, и взаимная информация. Выбор меры сходства зависит от того, относятся ли изображения к одной модальности; шум захвата также может сыграть роль в этом решении. Например, SSD - оптимальная мера сходства для изображений одной модальности с Гауссов шум.[20] Однако статистика изображений в ультразвуке значительно отличается от гауссовского шума, что приводит к введению специфических для ультразвука критериев сходства.[21] Мультимодальная регистрация требует более сложной меры сходства; в качестве альтернативы может использоваться другое представление изображения, например структурное представление[22] или регистрация смежной анатомии.[23][24]
- В процедура оптимизации. Либо непрерывный или же дискретная оптимизация выполняется. Для непрерывной оптимизации оптимизация на основе градиента применяются методы для повышения скорости сходимости.
Визуализация
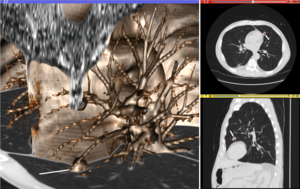
Визуализация играет несколько ключевых ролей в вычислении медицинских изображений. Методы из научная визуализация используются для понимания и передачи медицинских изображений, которые по своей сути пространственно-временны. Визуализация данных и анализ данных используются на неструктурированные данные формы, например, при оценке статистических показателей, полученных в ходе алгоритмической обработки. Прямое взаимодействие с данными, ключевой особенностью процесса визуализации, используется для выполнения визуальных запросов к данным, аннотирования изображений, управления процессами сегментации и регистрации и управления визуальным представлением данных (путем управления свойствами визуализации освещения и параметрами просмотра). Визуализация используется как для первоначального исследования, так и для передачи промежуточных и окончательных результатов анализа.
Рисунок «Визуализация медицинской визуализации» иллюстрирует несколько типов визуализации: 1. отображение поперечных сечений в виде изображений в градациях серого; 2. переформатированные виды изображений в градациях серого (сагиттальный вид в этом примере имеет другую ориентацию, чем исходное направление получения изображения; и 3. A 3D-рендеринг тех же данных. Узловое поражение четко видно на разных изображениях и отмечено белой линией.
Атласы
Медицинские изображения могут значительно различаться у разных людей из-за того, что у людей есть органы разных форм и размеров. Поэтому представление медицинских изображений для учета этой изменчивости имеет решающее значение. Популярный подход к представлению медицинских изображений - использование одного или нескольких атласов. Здесь атлас относится к конкретной модели для совокупности изображений с параметрами, полученными из набора обучающих данных.[25][26]
Самый простой пример атласа - изображение средней яркости, обычно называемое шаблоном. Однако атлас может также включать в себя более обширную информацию, такую как статистика локального изображения и вероятность того, что конкретное пространственное местоположение имеет определенную метку. Новые медицинские изображения, которые не используются во время обучения, можно сопоставить с атласом, который был адаптирован для конкретного приложения, например сегментация и групповой анализ. Сопоставление изображения с атласом обычно включает регистрация изображение и атлас. Эта деформация может использоваться для устранения вариабельности медицинских изображений.
Единый шаблон
Самый простой подход - смоделировать медицинские изображения как деформированные версии одного шаблона изображения. Например, анатомические МРТ-сканирование головного мозга часто сопоставляются с шаблоном MNI. [27] чтобы представить все снимки мозга в общих координатах. Главный недостаток подхода с одним шаблоном заключается в том, что при наличии значительных различий между шаблоном и данным тестовым изображением может не оказаться хорошего способа сопоставить одно изображение с другим. Например, анатомическое МРТ-сканирование мозга пациента с серьезными аномалиями головного мозга (то есть опухолью или хирургической процедурой) не может быть легко сопоставлено с шаблоном MNI.
Несколько шаблонов
Вместо того, чтобы полагаться на один шаблон, можно использовать несколько шаблонов. Идея состоит в том, чтобы представить изображение как деформированную версию одного из шаблонов. Например, может быть один шаблон для здорового населения и один шаблон для заболевшего. Однако во многих приложениях неясно, сколько шаблонов необходимо. Простой, хотя и дорогостоящий с точки зрения вычислений способ справиться с этим - сделать каждое изображение в наборе обучающих данных шаблоном, и, таким образом, каждое новое обнаруженное изображение сравнивается с каждым изображением в наборе обучающих данных. Более новый подход позволяет автоматически находить необходимое количество шаблонов.[28]
статистический анализ
Статистические методы объединяют область медицинской визуализации с современными Компьютерное зрение, Машинное обучение и Распознавание образов. За последнее десятилетие несколько больших наборов данных стали общедоступными (см., Например, ADNI, Проект «1000 функциональных коннектомов»), отчасти благодаря сотрудничеству между различными институтами и исследовательскими центрами. Это увеличение объема данных требует новых алгоритмов, которые могут анализировать и обнаруживать тонкие изменения в изображениях для решения клинических вопросов. Такие клинические вопросы очень разнообразны и включают групповой анализ, визуализацию биомаркеров, фенотипирование болезни и продольные исследования.
Групповой анализ
В групповом анализе цель состоит в том, чтобы обнаружить и количественно оценить отклонения, вызванные заболеванием, путем сравнения изображений двух или более когорт. Обычно одна из этих когорт состоит из нормальных (контрольных) субъектов, а другая - из пациентов с отклонениями от нормы. Вариация, вызванная заболеванием, может проявляться аномальной деформацией анатомии (см. Морфометрия на основе вокселей). Например, сокращение подкорковых тканей, таких как Гиппокамп в мозгу может быть связано с Болезнь Альцгеймера. Кроме того, изменения биохимической (функциональной) активности можно наблюдать с помощью таких методов визуализации, как Позитронно-эмиссионная томография.
Сравнение между группами обычно проводится по воксель уровень. Следовательно, самый популярный конвейер предварительной обработки, особенно в нейровизуализация, преобразует все изображения в наборе данных в общую систему координат с помощью (Регистрация медицинских изображений), чтобы поддерживать соответствие между вокселями. Учитывая это соответствие по вокселям, наиболее распространенным Частотник метод состоит в том, чтобы извлечь статистику для каждого воксела (например, среднюю интенсивность вокселов для каждой группы) и выполнить статистическая проверка гипотез чтобы оценить, поддерживается ли нулевая гипотеза. Нулевая гипотеза обычно предполагает, что две когорты взяты из одного и того же распределения и, следовательно, должны иметь одинаковые статистические свойства (например, средние значения двух групп равны для определенного воксела). Поскольку медицинские изображения содержат большое количество вокселей, проблема множественное сравнение необходимо решить.[29][30] Это также Байесовский подходы к решению проблемы группового анализа.[31]
Классификация
Хотя групповой анализ может количественно оценить общие эффекты патологии на анатомию и функцию, он не обеспечивает измерений на уровне субъектов и, следовательно, не может использоваться в качестве биомаркеров для диагностики (см. Биомаркеры визуализации). Клиницисты, с другой стороны, часто заинтересованы в ранней диагностике патологии (т. Е. Классификации,[32][33]) и в изучении прогрессирования заболевания (т.е. [34]). С методологической точки зрения современные методы варьируются от применения стандартных алгоритмов машинного обучения до наборов данных медицинской визуализации (например, Машина опорных векторов [35]), к разработке новых подходов, адаптированных к потребностям отрасли.[36] Основные трудности заключаются в следующем:
- Небольшой размер выборки (Проклятие размерности): большой набор данных медицинской визуализации содержит от сотен до тысяч изображений, тогда как количество вокселей в типичном объемном изображении может легко превысить миллионы. Решением этой проблемы является уменьшение количества функций в информативном смысле (см. уменьшение размерности). Несколько неконтролируемых и полу- / контролируемых,[36][37][38][39] были предложены подходы к решению этой проблемы.
- Интерпретируемость: хорошая точность обобщения не всегда является основной целью, поскольку врачи хотели бы понять, какие части анатомии затронуты заболеванием. Поэтому интерпретируемость результатов очень важна; методы, игнорирующие структуру изображения, не приветствуются. Альтернативные методы на основе выбор функции Были предложены,.[37][38][39][40]
Кластеризация
Методы классификации паттернов на основе изображений обычно предполагают, что неврологические эффекты заболевания отчетливы и четко определены. Это может быть не всегда. По ряду заболеваний популяции пациентов очень разнородны, и дальнейшая категоризация на подусловия не установлена. Кроме того, некоторые заболевания (например, расстройство аутистического спектра (ASD), шизофрения, легкие когнитивные нарушения (MCI)) может характеризоваться непрерывным или почти непрерывным спектром от легкого когнитивного нарушения до очень выраженных патологических изменений. Чтобы облегчить анализ гетерогенных расстройств на основе изображений, были разработаны методологические альтернативы классификации паттернов. Эти методы заимствуют идеи из многомерной кластеризации. [41] и многомерная регрессия паттернов для объединения данной популяции в однородные субпопуляции. Цель состоит в том, чтобы обеспечить лучшее количественное понимание болезни в каждой подгруппе населения.
Анализ формы
Анализ формы это область обработки медицинских изображений, изучающая геометрический свойства конструкций, полученных из различных методы визуализации. Анализ формы в последнее время вызывает все больший интерес у медицинского сообщества из-за его способности точно определять местоположение морфологический изменения между различными популяциями структур, то есть здоровыми и патологическими, женщинами и мужчинами, молодыми и пожилыми. Анализ формы включает два основных этапа: соответствие форм и статистический анализ.
- Соответствие форм - это методология, которая вычисляет соответствующие местоположения между геометрическими фигурами, представленными треугольными сетками, контурами, наборами точек или объемными изображениями. Очевидно, что определение соответствия напрямую повлияет на анализ. Среди различных вариантов структур соответствия мы можем найти: анатомическое соответствие, ручные ориентиры, функциональное соответствие (т.е. в локусе морфометрии мозга, отвечающем за одинаковые нейронные функции), геометрическое соответствие, (для объемов изображений) сходство интенсивности и т. Д. Некоторые подходы, например спектральный анализ формы, не требует соответствия, а сравнивает дескрипторы формы напрямую.
- Статистический анализ предоставит измерения структурных изменений в соответствующих местах.
Продольные исследования
В лонгитюдных исследованиях один и тот же человек отображается повторно. Эта информация может быть включена как в анализ изображений, а также в статистическое моделирование.
- При продольной обработке изображений методы сегментации и анализа отдельных моментов времени информируются и упорядочиваются с помощью общей информации, обычно из внутриобъектного шаблона. Эта регуляризация предназначена для уменьшения шума измерения и, таким образом, помогает повысить чувствительность и статистическую мощность. В то же время необходимо избегать чрезмерной регуляризации, чтобы размеры эффекта оставались стабильными. Например, интенсивная регуляризация может привести к превосходной надежности повторного тестирования, но ограничивает возможность обнаружения любых истинных изменений и различий между группами. Часто необходимо найти компромисс, который оптимизирует снижение шума за счет ограниченной потери размера эффекта. Другой распространенной проблемой при обработке продольных изображений является, часто непреднамеренное, смещение обработки. Когда, например, последующие изображения регистрируются и повторно дискретизируются в базовое изображение, артефакты интерполяции появляются только в последующих изображениях, а не в базовом. Эти артефакты могут вызывать ложные эффекты (обычно это склонность к переоценке продольных изменений и, таким образом, к недооценке требуемого размера выборки). Поэтому важно, чтобы все точки обрабатывались точно так же, чтобы избежать ошибок обработки.
- Постобработка и статистический анализ продольных данных обычно требует специальных статистических инструментов, таких как ANOVA с повторными измерениями или более мощные линейные модели смешанных эффектов. Кроме того, выгодно учитывать пространственное распределение сигнала. Например, измерения толщины кортикального слоя покажут корреляцию внутри субъекта во времени, а также в пределах области на корковой поверхности - факт, который можно использовать для увеличения статистической мощности. Кроме того, анализ времени до события (он же выживаемость) часто используется для анализа продольных данных и определения значимых предикторов.
Физиологическое моделирование на основе изображений
Традиционно обработка медицинских изображений направлена на количественную оценку и объединение структурной или функциональной информации, доступной в момент и время получения изображения. В этом отношении его можно рассматривать как количественное восприятие основных анатомических, физических или физиологических процессов. Однако в последние несколько лет растет интерес к прогностической оценке заболевания или курса терапии. Таким образом, моделирование на основе изображений, будь то биомеханическое или физиологическое моделирование, может расширить возможности вычисления изображений с описательной до прогнозной.
Согласно дорожной карте исследования STEP,[42][43] в Виртуальный физиологический человек (VPH) - это методологическая и технологическая основа, которая после создания позволит исследовать человеческое тело как единую сложную систему. Основываясь на концепции VPH, Международный союз физиологических наук (IUPS) спонсирует IUPS Physiome Project более десяти лет.[44][45] Это всемирно известная попытка предоставить вычислительную основу для понимания физиологии человека. Он направлен на разработку интегративных моделей на всех уровнях биологической организации, от генов до целых организмов через генные регуляторные сети, белковые пути, интегративные функции клеток и взаимосвязи между структурой и функцией тканей и всего органа. Такой подход направлен на преобразование современной медицинской практики и лежит в основе новой эры вычислительной медицины.[46]
В этом контексте медицинская визуализация и обработка изображений играют все более важную роль, поскольку они предоставляют системы и методы для визуализации, количественной оценки и объединения структурной и функциональной информации о человеке in vivo. Эти две обширные области исследований включают преобразование общих вычислительных моделей для представления конкретных предметов, тем самым открывая путь для персонализированных вычислительных моделей.[47] Индивидуализация общих вычислительных моделей посредством построения изображений может быть реализована в трех дополнительных направлениях:
- определение предметной вычислительной области (анатомии) и связанных субдоменов (типов тканей);
- определение граничных и начальных условий из (динамического и / или функционального) изображения; и
- характеристика структурных и функциональных свойств тканей.
Кроме того, визуализация также играет ключевую роль в оценке и валидации таких моделей как на людях, так и на животных моделях, а также в переводе моделей в клинические условия как для диагностических, так и для терапевтических целей. В этом конкретном контексте молекулярная, биологическая и доклиническая визуализация предоставляют дополнительные данные и понимание базовой структуры и функции в молекулах, клетках, тканях и моделях животных, которые могут быть перенесены в физиологию человека, где это необходимо.
Применение моделей VPH / Physiome на основе изображений в базовой и клинической областях обширно. Вообще говоря, они обещают стать новыми виртуальные методы визуализации. Фактически будет отображено больше, часто ненаблюдаемых, параметров. in silico основан на интеграции наблюдаемых, но иногда разреженных и противоречивых мультимодальных изображений и физиологических измерений. Вычислительные модели будут служить для интерпретации измерений в соответствии с основными биофизическими, биохимическими или биологическими законами исследуемых физиологических или патофизиологических процессов. В конечном итоге такие исследовательские инструменты и системы помогут нам понять процессы заболевания, естественную историю развития болезни и влияние фармакологических и / или интервенционных терапевтических процедур на течение болезни.
Взаимодействие между визуализацией и моделированием выходит за рамки интерпретации измерений в соответствии с физиологией. Моделирование на основе изображений, ориентированное на пациента, в сочетании с моделями медицинских устройств и фармакологической терапии, открывает путь к прогнозирующей визуализации, благодаря которой можно будет понять, спланировать и оптимизировать такие вмешательства. in silico.
Математические методы в медицинской визуализации
Ряд сложных математических методов вошел в медицинскую визуализацию и уже реализован в различных пакетах программного обеспечения. К ним относятся подходы, основанные на уравнения в частных производных (PDE) и управляемые кривизной потоки для улучшения, сегментации и регистрации. Поскольку они используют PDE, методы можно распараллелить и реализовать на GPGPU. Некоторые из этих методов были вдохновлены идеями оптимальный контроль. Соответственно, совсем недавно идеи из контроля недавно стали использоваться в интерактивных методах, особенно в сегментации. Более того, из-за шума и необходимости методов статистической оценки для более динамично изменяющихся изображений Фильтр Калмана [48] и фильтр твердых частиц вошли в обиход. Обзор этих методов с обширным списком ссылок можно найти в.[49]
Вычисления, специфичные для модальности
Некоторые методы визуализации предоставляют очень специализированную информацию. Полученные изображения нельзя рассматривать как обычные скалярные изображения, и они дают начало новым подобластям обработки медицинских изображений. Примеры включают диффузная МРТ,функциональная МРТ и другие.
Диффузная МРТ
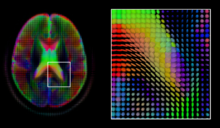
Диффузная МРТ структурный магнитно-резонансная томография модальность, позволяющая измерять процесс диффузии молекул. Диффузия измеряется путем приложения градиентного импульса к магнитному полю в определенном направлении. В типичном сборе данных набор равномерно распределенных направлений градиента используется для создания набора взвешенных по диффузии объемов. Кроме того, невзвешенный объем получается в том же магнитном поле без применения градиентного импульса. Поскольку каждое приобретение связано с несколькими томами, диффузная МРТ создал множество уникальных задач в области обработки медицинских изображений.
В медицине есть две основные вычислительные цели: диффузная МРТ:
- Оценка местных свойств ткани, таких как коэффициент диффузии;
- Оценка локальных направлений и глобальных путей распространения.
В тензор диффузии,[50] симметричный 3 × 3 положительно определенная матрица, предлагает простое решение для обеих этих целей.Он пропорционален ковариационной матрице нормально распределенного профиля локальной диффузии и, таким образом, доминирующий собственный вектор этой матрицы является главным направлением локальной диффузии. Из-за простоты этой модели оценка максимального правдоподобия тензора диффузии может быть получена простым решением системы линейных уравнений в каждом месте независимо. Однако, поскольку предполагается, что объем содержит смежные тканевые волокна, может быть предпочтительнее оценить объем тензоров диффузии в целом, наложив условия регулярности на лежащее в основе поле тензоров.[51] Скалярные значения могут быть извлечены из тензора диффузии, например фракционная анизотропия, средняя, осевая и радиальная коэффициенты диффузии, которые косвенно измерять свойства тканей, такие как дисмиелинизация аксональных волокон [52] или наличие отеков.[53] Стандартные методы вычисления скалярных изображений, такие как регистрация и сегментация, могут применяться непосредственно к объемам таких скалярных значений. Однако, чтобы полностью использовать информацию в тензоре диффузии, эти методы были адаптированы для учета тензорных объемов при выполнении регистрации. [54][55] и сегментация.[56][57]
Учитывая главное направление диффузии в каждом месте объема, можно оценить глобальные пути диффузии с помощью процесса, известного как трактография.[58] Однако из-за относительно низкого разрешения диффузная МРТмногие из этих путей могут пересекаться, целоваться или развеиваться в одном месте. В этой ситуации единственное главное направление тензор диффузии не является подходящей моделью для локального распределения диффузии. Наиболее распространенное решение этой проблемы - оценка нескольких направлений локальной диффузии с использованием более сложных моделей. К ним относятся смеси тензоров диффузии,[59] Визуализация Q-шара,[60] визуализация спектра диффузии [61] и функции распределения ориентации волокон,[62][63] которые обычно требуют ХАРДИ получение с большим количеством направлений градиента. Как и в случае с тензором диффузии, объемы, оцениваемые с помощью этих сложных моделей, требуют специальной обработки при применении методов вычисления изображений, таких как постановка на учет [64][65][66] и сегментация.[67]
Функциональная МРТ
Функциональная магнитно-резонансная томография (фМРТ) это метод медицинской визуализации, который косвенно измеряет нейронную активность, наблюдая за локальными гемодинамика, или сигнал зависимости уровня кислорода в крови (ЖИРНЫЙ). Данные фМРТ предлагают ряд инсайтов, и их можно условно разделить на две категории:
- ФМРТ, связанная с задачей приобретается, когда субъект выполняет последовательность временных экспериментальных условий. В экспериментах с блочным дизайном условия присутствуют в течение коротких периодов времени (например, 10 секунд) и чередуются с периодами отдыха. Эксперименты, связанные с событиями, основываются на случайной последовательности стимулов и используют одну временную точку для обозначения каждого условия. Стандартный подход к анализу фМРТ, относящегося к задаче - это общая линейная модель (GLM) [68]
- ФМРТ в состоянии покоя приобретается при отсутствии экспериментальной задачи. Обычно цель состоит в изучении внутренней сетевой структуры мозга. Наблюдения, сделанные во время отдыха, также были связаны с конкретными когнитивными процессами, такими как кодирование или отражение. Большинство исследований фМРТ в состоянии покоя сосредоточено на низкочастотных колебаниях сигнала фМРТ (LF-BOLD). Семенные открытия включают сеть по умолчанию,[69] комплексная кортикальная парцелляция,[70] и привязка сетевых характеристик к поведенческим параметрам.
Существует широкий набор методологий, используемых для анализа данных функциональной нейровизуализации, и часто нет единого мнения относительно Лучший метод. Вместо этого исследователи подходят к каждой проблеме независимо и выбирают подходящую модель / алгоритм. В этом контексте наблюдается относительно активный обмен между нейробиология, вычислительная биология, статистика, и машинное обучение сообщества. Известные подходы включают:
- Массивные одномерные подходы которые исследуют отдельные воксели в данных изображений на предмет их взаимосвязи с условиями эксперимента. Главный подход - это общая линейная модель (GLM) [68]
- Подходы на основе многомерных и классификаторов, часто называемый многовоксельным анализом паттернов или многовариантным анализом паттернов, исследует данные на предмет глобальных и потенциально распределенных реакций на экспериментальные условия. Используемые ранние подходы опорные векторные машины (SVM) для изучения реакции на визуальные раздражители.[71] Недавно были исследованы альтернативные алгоритмы распознавания образов, такие как случайный лес на основе контраста Джини [72] или редкая регрессия и изучение словаря [73]
- Функциональный анализ связности изучает внутреннюю сетевую структуру мозга, в том числе взаимодействия между регионами. Большинство таких исследований сосредоточено на данных о состоянии покоя, которые распространяются на мозг. [70] или найти корреляты поведенческих мер.[74] Данные по конкретной задаче можно использовать для изучения причинно-следственных связей между областями мозга (например, динамическое картирование причинно-следственных связей (DCM) [75]).
При работе с большими когортами субъектов очень важна нормализация (регистрация) отдельных субъектов в общей системе отсчета. Существует множество работ и инструментов для выполнения нормализации на основе анатомии (FSL, FreeSurfer, SPM). Согласование с учетом пространственной изменчивости по предметам - более новое направление работы. Примерами являются выравнивание коры на основе корреляции сигналов фМРТ,[76] выравнивание на основе глобальной функциональной структуры связности как в данных о задачах, так и в данных состояния покоя,[77] и выравнивание на основе профилей активации конкретных стимулов отдельных вокселей.[78]
Программного обеспечения
Программное обеспечение для обработки медицинских изображений представляет собой сложную комбинацию систем, обеспечивающих ввод-вывод, визуализацию и взаимодействие, пользовательский интерфейс, управление данными и вычисления. Обычно системные архитектуры имеют многоуровневую структуру для обслуживания разработчиков алгоритмов, разработчиков приложений и пользователей. Нижние уровни часто представляют собой библиотеки и / или наборы инструментов, которые обеспечивают базовые вычислительные возможности; в то время как верхние слои представляют собой специализированные приложения, которые решают конкретные медицинские проблемы, заболевания или системы организма.
Дополнительные примечания
Вычисление медицинских изображений также относится к области Компьютерное зрение. Международное общество, Общество MICCAI представляет поле и организует ежегодную конференцию и связанные с ней семинары. Материалы конференции публикуются Springer в серии Lecture Notes in Computer Science.[79] В 2000 г. Н. Аяче и Дж. Дункан проанализировали состояние отрасли.[80]
Смотрите также
Рекомендации
- ^ Forghani, M .; Forouzanfar, M .; Тешнехлаб, М. (2010). «Оптимизация параметров улучшенного алгоритма кластеризации нечетких c-средних для сегментации МРТ изображений мозга». Инженерные приложения искусственного интеллекта. 23 (2): 160–168. Дои:10.1016 / j.engappai.2009.10.002.
- ^ Джей Джи; M Reivich; Р. Байчи (1993). «Упругое деформирование трехмерного атласа для соответствия анатомическим изображениям мозга». Журнал компьютерной томографии. 17 (1): 225–236. Дои:10.1097/00004728-199303000-00011. PMID 8454749.
- ^ MR Sabuncu; BT Yeo; К. Ван Лемпут; B Fischl; П. Голланд (июнь 2010 г.). «Генеративная модель для сегментации изображений на основе слияния этикеток». IEEE Transactions по медицинской визуализации. 29 (10): 1714–1729. Дои:10.1109 / TMI.2010.2050897. ЧВК 3268159. PMID 20562040.
- ^ Кутс Т.Ф., Тейлор С.Дж., Купер Д.Х., Грэм Дж. (1995). «Активные фигурные модели - их обучение и применение». Компьютерное зрение и понимание изображений. 61 (1): 38–59. Дои:10.1006 / cviu.1995.1004.
- ^ Cootes, T.F .; Эдвардс, G.J .; Тейлор, Си-Джей (2001). «Модели активного внешнего вида». IEEE Transactions по анализу шаблонов и машинному анализу. 23 (6): 681–685. CiteSeerX 10.1.1.128.4967. Дои:10.1109/34.927467.
- ^ Г. Чжэн; С. Ли; Г. Секели (2017). Статистический анализ формы и деформации. Академическая пресса. ISBN 9780128104941.
- ^ Р. Гольденберг, Р. Киммель, Э. Ривлин и М. Рудский (2001). «Быстрые геодезические активные контуры» (PDF). IEEE Transactions по обработке изображений. 10 (10): 1467–1475. Bibcode:2001ITIP ... 10.1467G. CiteSeerX 10.1.1.35.1977. Дои:10.1109/83.951533. PMID 18255491.CS1 maint: несколько имен: список авторов (связь)
- ^ Карасев, П .; Колесов И .; Чуды, К .; Vela, P .; Танненбаум, А. (2011). Интерактивная сегментация МРТ с управляемым активным зрением. Материалы конференции по решению и контролю. С. 2293–2298. Дои:10.1109 / CDC.2011.6161453. ISBN 978-1-61284-801-3. ЧВК 3935399. PMID 24584213.
- ^ К. Микула, Н. Пейриерас, М. Ремешикова, А. Сарти: Сегментация трехмерного изображения эмбриогенеза методом обобщенной субъективной поверхности с использованием метода конечных объемов. Материалы 5-го Международного симпозиума FVCA5 по конечным объемам для сложных приложений, Hermes Publ., Париж, 2008.
- ^ А. Сарти, Дж. Читти: субъективные поверхности и потоковые графы римановой средней кривизны // Acta Math. Univ. Коменский. (Н.С.) 70 (2000), 85–103.
- ^ А. Сарти, Р. Маллади, Дж. А. Сетиан: Субъективные поверхности: метод завершения отсутствующих границ. Proc. Nat. Акад. Sci. mi 12, No. 97 (2000), 6258–6263.
- ^ А. Сарти, Р. Маллади, Дж. А. Сетиан: Субъективные поверхности: геометрическая модель для завершения границ, Международный журнал компьютерного зрения, mi 46, № 3 (2002), 201–221.
- ^ Эхсани Рад, Абдолвахаб; Мохд Рахим Мохд Шафри; Рехман Амджад; Альтамим Айман; Саба Танзила (май 2013 г.). «Оценка современных подходов к сегментации стоматологических рентгенограмм в компьютерных приложениях». Технический обзор IETE. 30 (3): 210. Дои:10.4103/0256-4602.113498.
- ^ Лиза Готтесфельд Браун (1992). «Обзор методов совмещения изображений». Опросы ACM Computing. 24 (4): 325–376. CiteSeerX 10.1.1.35.2732. Дои:10.1145/146370.146374.
- ^ Дж. Майнц; М. Виергевер (1998). «Обзор регистрации медицинских изображений». Анализ медицинских изображений. 2 (1): 1–36. CiteSeerX 10.1.1.46.4959. Дои:10.1016 / S1361-8415 (01) 80026-8. PMID 10638851.
- ^ Дж. Хайнал; Д. Хоукс; Д. Хилл (2001). Регистрация медицинских изображений. Батон-Руж, Флорида: CRC Press.
- ^ Барбара Зитова; Ян Флюссер (2003). «Методы регистрации изображений: опрос». Image Vision Comput. 21 (11): 977–1000. Дои:10.1016 / S0262-8856 (03) 00137-9. HDL:10338.dmlcz / 141595.
- ^ J. P. W. Pluim; Дж. Б. А. Майнц; М. А. Виергевер (2003). «Взаимная информационная регистрация медицинских изображений: Обследование». IEEE Trans. Med. Изображения. 22 (8): 986–1004. CiteSeerX 10.1.1.197.6513. Дои:10.1109 / TMI.2003.815867. PMID 12906253.
- ^ Гренандер, Ульф; Миллер, Майкл И. (1998). «Вычислительная анатомия: новая дисциплина». В. Прил. Математика. LVI (4): 617–694. Дои:10.1090 / qam / 1668732.
- ^ П. А. Виола (1995). Согласование путем максимизации взаимной информации (Тезис). Массачусетский Институт Технологий.
- ^ К. Вахингер; Т. Кляйн; Н. Наваб (2011). «Локально адаптивные меры ультразвукового сходства на основе Накагами». Ультразвук. 52 (4): 547–554. Дои:10.1016 / j.ultras.2011.11.009. PMID 22197152.
- ^ К. Вахингер; Н. Наваб (2012). «Энтропийные и лапласовские изображения: структурные представления для мультимодального совмещения». Анализ медицинских изображений. 16 (1): 1–17. Дои:10.1016 / j.media.2011.03.001. PMID 21632274.
- ^ Хилл, Дерек LG; Хоукс, Дэвид Дж (1994-04-01). «Регистрация медицинских изображений с использованием знания смежности анатомических структур». Вычисления изображений и зрения. 12 (3): 173–178. CiteSeerX 10.1.1.421.5162. Дои:10.1016/0262-8856(94)90069-8. ISSN 0262-8856.
- ^ Тот, Даниил; Панайоту, Мария; Брост, Александр; Бехар, Джонатан М .; Ринальди, Кристофер А .; Rhode, Kawal S .; Маунтни, Питер (2016-10-17). Регистрация с соседними анатомическими структурами для кардио-ресинхронизирующей терапии.. Статистические атласы и вычислительные модели сердца. Проблемы визуализации и моделирования (Представлена рукопись). Конспект лекций по информатике. С. 127–134. Дои:10.1007/978-3-319-52718-5_14. ISBN 9783319527178.
- ^ М. Де Крен; A. B. d Aische; Б. Макк; С. К. Варфилд (2004). «Многопрофильная регистрация для построения объективного статистического атласа» (PDF). Слушания по медицинской обработке изображений и компьютерному вмешательству 2004 г.. Конспект лекций по информатике. 3216: 655–662. Дои:10.1007/978-3-540-30135-6_80. ISBN 978-3-540-22976-6.
- ^ К. Дж. Твининг; Т. Кутс; С. Марсланд; В. Петрович; Р. Шестовиц; К. Тейлор (2005). «Единый теоретико-информационный подход к групповой нежесткой регистрации и построению моделей». Труды обработки информации в медицинской визуализации 2005 г.. Конспект лекций по информатике. 19: 1–14. Дои:10.1007/11505730_1. ISBN 978-3-540-26545-0. PMID 17354680.
- ^ «Мозг MNI и атлас Талаирах».
- ^ М. Сабунку; С. К. Бальчи; М. Э. Шентон; П. Голланд (2009). «Анализ населения на основе изображений посредством моделирования смеси». IEEE Transactions по медицинской визуализации. 28 (9): 1473–1487. CiteSeerX 10.1.1.158.3690. Дои:10.1109 / TMI.2009.2017942. ЧВК 2832589. PMID 19336293.
- ^ Дж. Эшбернер; К.Дж. Фристон (2000). "Морфометрия на основе вокселей - методы". NeuroImage. 11 (6): 805–821. CiteSeerX 10.1.1.114.9512. Дои:10.1006 / nimg.2000.0582. PMID 10860804.
- ^ К. Давацикос (2004). «Почему морфометрический анализ на основе вокселей следует использовать с большой осторожностью при характеристике групповых различий». NeuroImage. 23 (1): 17–20. Дои:10.1016 / j.neuroimage.2004.05.010. PMID 15325347.
- ^ К.Дж. Фристон; W.D. Пенни; К. Филлипс; С.Дж. Кибель; Г. Хинтон; Дж. Эшбёрнер (2002). «Классический и байесовский вывод в нейровизуализации: теория». NeuroImage. 16 (2): 465–483. CiteSeerX 10.1.1.128.8333. Дои:10.1006 / nimg.2002.1090. PMID 12030832.
- ^ Юн Фань; Нематолла Батмангхелич; Крис М. Кларк; Христос Давацикос (2008). «Пространственные паттерны атрофии головного мозга у пациентов с MCI, идентифицированные с помощью классификации паттернов большого размера, предсказывают последующее снижение когнитивных функций». NeuroImage. 39 (4): 1731–1743. Дои:10.1016 / j.neuroimage.2007.10.031. ЧВК 2861339. PMID 18053747.
- ^ Реми Куэнгне; Эмили Жерардин; Жером Тессиерас; Гийом Аузиас; Стефан Лехериси; Мари-Одиль Абер; Мари Чупен; Хабиб Бенали; Оливье Коллио (2011). «Инициатива по нейровизуализации болезни Альцгеймера, Автоматическая классификация пациентов с болезнью Альцгеймера на основе структурной МРТ: сравнение десяти методов с использованием базы данных ADNI» (PDF). NeuroImage. 56 (2): 766–781. Дои:10.1016 / j.neuroimage.2010.06.013. PMID 20542124.
- ^ Ю. Ван; Ю. Фан; P. Bhatt P; К. Давацикос (2010). «Регрессия многомерных паттернов с использованием машинного обучения: от медицинских изображений до непрерывных клинических переменных». NeuroImage. 50 (4): 1519–35. Дои:10.1016 / j.neuroimage.2009.12.092. ЧВК 2839056. PMID 20056158.
- ^ Бенуа Маньен; Лилия Месроб; Серж Кинкингнехун; Мелани Пелегрини-Иссак; Оливье Коллио; Мари Саразин; Бруно Дюбуа; Стефан Лехериси; Хабиб Бенали (2009). «Поддержка машинной классификации болезни Альцгеймера на основе анатомической МРТ всего мозга». Нейрорадиология. 51 (2): 73–83. Дои:10.1007 / s00234-008-0463-x. PMID 18846369.
- ^ а б Н.К. Батмангхелич; Б. Таскар; К. Давацикос (2012). «Генеративно-дискриминантное базовое обучение для медицинской визуализации». IEEE Trans Med Imaging. 31 (1): 51–69. Дои:10.1109 / TMI.2011.2162961. ЧВК 3402718. PMID 21791408.
- ^ а б Гленн Фанг; Джонатан Стоукель (2007). «Выбор характеристик SVM для классификации изображений SPECT болезни Альцгеймера с использованием пространственной информации». Знания и информационные системы. 11 (2): 243–258. CiteSeerX 10.1.1.62.6245. Дои:10.1007 / s10115-006-0043-5.
- ^ а б Р. Чавес; Х. Рамирес; J.M. Górriz; М. Лопес; Д. Салас-Гонсалес; И. Альварес; Ф. Сеговия (2009). «Компьютерная диагностика болезни Альцгеймера на основе SVM с использованием t-критерия выбора признаков NMSE с корреляционным взвешиванием признаков». Письма о неврологии. 461 (3): 293–297. Дои:10.1016 / j.neulet.2009.06.052. PMID 19549559.
- ^ а б Яньси Лю; Леонид Теверовский; Оуэн Кармайкл; Рон Кикинис; Марта Шентон; Кэмерон С. Картер; В. Эндрю Стенджер; Саймон Дэвис; Говард Айзенштейн; Джеймс Т. Беккер (2004). «Дискриминационный анализ МР-изображений для автоматической классификации шизофрении и болезни Альцгеймера» (PDF). Компьютерная обработка изображений и компьютерное вмешательство - Миччай. Конспект лекций по информатике. 3216: 393–401. Дои:10.1007/978-3-540-30135-6_48. ISBN 978-3-540-22976-6.
- ^ Savio A .; Гранья М. (2013). «Выбор функции на основе деформации для компьютерной диагностики болезни Альцгеймера». Экспертные системы с приложениями. 40 (5): 1619–1628. Дои:10.1016 / j.eswa.2012.09.009. ISSN 0957-4174.
- ^ Р. Филипович; С. М. Резник; К. Давацикос (2011). «Полу-контролируемый кластерный анализ данных изображений». NeuroImage. 54 (3): 2185–2197. Дои:10.1016 / j.neuroimage.2010.09.074. ЧВК 3008313. PMID 20933091.
- ^ Дорожная карта исследования STEP В архиве 2008-08-28 на Wayback Machine. europhysiome.org
- ^ Дж. У. Феннер; Б. Брук; Г. Клэпворси; П. В. Ковени; В. Фейпель; Х. Грегерсен; Д. Р. Хосе; П. Коль; П. Лоуфорд; К. М. Маккормак; Д. Пинни; С. Р. Томас; С. Ван Синт Ян; С. Уотерс; М. Висконти (2008). «EuroPhysiome, STEP и дорожная карта для виртуального физиологического человека» (PDF). Философские труды Королевского общества A. 366 (1878): 2979–2999. Bibcode:2008RSPTA.366.2979F. Дои:10.1098 / рста.2008.0089. PMID 18559316.
- ^ Дж. Б. Бассингтуэйт (2000). «Стратегии проекта Physiome». Анна. Биомед. Англ.. 28 (8): 1043–1058. Дои:10.1114/1.1313771. ЧВК 3425440. PMID 11144666.
- ^ П. Дж. Хантер; Т. К. Борг (2003). «Интеграция белков в органы: проект Physiome». Nat. Преподобный Мол. Cell Biol. 4 (3): 237–243. Дои:10.1038 / nrm1054. PMID 12612642.
- ^ Р. Л. Уинслоу; Н. Траянова; Д. Геман; М. И. Миллер (2012). «Компьютерная медицина: перевод моделей в клиническую практику». Sci. Пер. Med. 4 (158): 158rv11. Дои:10.1126 / scitranslmed.3003528. ЧВК 3618897. PMID 23115356.
- ^ Н. Аяче, Ж.-П. Boissel, S. Brunak, G. Clapworthy, G. Lonsdale, J. Fingberg, AF Frangi, G.Deco, PJ Hunter, P.Nielsen, M.Halstead, DR Hose, I. Magnin, F. Martin-Sanchez, P . Sloot, J. Kaandorp, A. Hoekstra, S. Van Sint Jan и M. Viceconti (2005) «К виртуальному физиологическому человеку: многоуровневое моделирование и симуляция анатомии и физиологии человека». Генеральный директорат INFSO и Генеральный директорат JRC, Белая книга
- ^ Boulfelfel D .; Рангаян Р.М .; Hahn L.J .; Kloiber R .; Кудувалли Г.Р. (1994). «Восстановление изображений однофотонной эмиссионной компьютерной томографии фильтром Калмана». IEEE Transactions по медицинской визуализации. 13 (1): 102–109. Дои:10.1109/42.276148. PMID 18218487.
- ^ Ангенент, С.; Pichon, E .; Танненбаум, А. (2006). «Математические методы обработки медицинских изображений». Бюллетень АПП. 43 (3): 365–396. Дои:10.1090 / S0273-0979-06-01104-9. ЧВК 3640423. PMID 23645963.
- ^ П. Бассер; Дж. Маттиелло; Д. ЛеБихан (январь 1994 г.). «МРТ диффузионная тензорная спектроскопия, визуализация». Биофизический журнал. 66 (1): 259–267. Bibcode:1994BpJ .... 66..259B. Дои:10.1016 / S0006-3495 (94) 80775-1. ЧВК 1275686. PMID 8130344.
- ^ П. Филлард; X Pennec; V Arsigny; Н Аяче (2007). «Клиническая оценка DT-MRI, сглаживание, отслеживание волокон с логарифмическими евклидовыми метриками». IEEE Transactions по медицинской визуализации. 26 (11): 1472–1482. CiteSeerX 10.1.1.218.6380. Дои:10.1109 / TMI.2007.899173. PMID 18041263.
- ^ S-K Song; Ю-З, вс; М. Рэмсботтом; C Cheng; Дж. Рассел; Крест (ноябрь 2002 г.). «Дисмиелинизация, выявленная с помощью МРТ, как увеличенная радиальная (но без изменений осевая) диффузия воды». NeuroImage. 13 (3): 1429–1436. Дои:10.1006 / nimg.2002.1267. PMID 12414282.
- ^ П. Барзо; Мармару; P Fatouros; К. Хаясаки; Ф Корвин (декабрь 1997 г.). «Вклад вазогенных и клеточных отеков в травматический отек мозга, измеренный с помощью диффузионно-взвешенной визуализации». Журнал нейрохирургии. 87 (6): 900–907. Дои:10.3171 / jns.1997.87.6.0900. PMID 9384402.
- ^ D Александр; C Pierpaoli; П. Бассер (январь 2001 г.). «Пространственная трансформация диффузно-тензорных магнитно-резонансных изображений» (PDF). IEEE Transactions по медицинской визуализации. 20 (11): 1131–1139. Дои:10.1109/42.963816. PMID 11700739.
- ^ Y Cao; М. Миллер; S Mori; Р. Уинслоу; Л. Юнес (июнь 2006 г.). «Диффеоморфное сопоставление диффузных тензорных изображений». Труды конференции IEEE Computer Society по компьютерному зрению, распознаванию образов (CVPR), семинару по математическим методам в биомедицинском анализе изображений (MMBIA 2006). Нью-Йорк. п. 67. Дои:10.1109 / CVPRW.2006.65. ЧВК 2920614.
- ^ Z Wang; Б. Вемури (октябрь 2005 г.). «Сегментация DTI с использованием теоретико-информационной меры различия тензорного тензора». IEEE Transactions по медицинской визуализации. 24 (10): 1267–1277. CiteSeerX 10.1.1.464.9059. Дои:10.1109 / TMI.2005.854516. PMID 16229414.
- ^ Melonakos, J .; Pichon, E .; Ангенент, С.; Танненбаум, А. (2008). «Активные контуры Финслера». IEEE Trans. ПАМИ. 30 (3): 412–423. Дои:10.1109 / TPAMI.2007.70713. ЧВК 2796633. PMID 18195436.
- ^ S Mori; B Crain; V Chacko; П. ван Зейл (февраль 1999 г.). «Трехмерное отслеживание проекций аксонов в головном мозге с помощью магнитно-резонансной томографии». Анналы неврологии. 45 (2): 265–269. Дои:10.1002 / 1531-8249 (199902) 45: 2 <265 :: AID-ANA21> 3.0.CO; 2-3. PMID 9989633.
- ^ D Tuch; Т. Риз; M Wiegell; Н. Макрис; J Belliveau; V Wedeen (октябрь 2002 г.). «Диффузионная визуализация с высоким угловым разрешением выявляет интравоксельную неоднородность волокон белого вещества». Магнитный резонанс в медицине. 48 (4): 577–582. Дои:10.1002 / mrm.10268. PMID 12353272.
- ^ Д. Туч (декабрь 2004 г.). «Визуализация Q-шара». Магнитный резонанс в медицине. 52 (6): 1358–1372. Дои:10.1002 / mrm.20279. PMID 15562495.
- ^ V Wedeen; П. Хагманн; W-Y Tseng; Т. Риз (декабрь 2005 г.). «Картирование сложной структуры ткани с помощью магнитно-резонансной томографии диффузного спектра». Магнитный резонанс в медицине. 54 (6): 1377–1386. Дои:10.1002 / mrm.20642. PMID 16247738.
- ^ К. Янсонс; D Александр (июль 2003 г.). «Стойкая угловая структура: новые выводы из данных диффузной магнитно-резонансной томографии». Труды обработки информации в медицинской визуализации (IPMI) 2003, LNCS 2732. С. 672–683. Дои:10.1007/978-3-540-45087-0_56.
- ^ J-D Tournier; Ф Каламанте; D Gadian; Коннелли (2007). «Прямая оценка функции плотности ориентации волокон по диффузионно-взвешенным данным МРТ с использованием сферической деконволюции». NeuroImage. 23 (3): 1176–1185. Дои:10.1016 / j.neuroimage.2004.07.037. PMID 15528117.
- ^ X Geng; Т. Росс; W Zhan; H Gu; Y-P Chao; C-P Lin; G Christensen; N Schuff; Ян Ян (июль 2009 г.). «Регистрация диффузионной МРТ с использованием функций распределения ориентации». Труды обработки информации в медицинской визуализации (IPMI) 2009, LNCS 5636. 21. С. 626–637. Дои:10.1007/978-3-642-02498-6_52. ЧВК 3860746.
- ^ П-Т Яп; Y Chen; H An; Ян Ян; Дж. Гилмор; W Lin; Д Шен (2011). «СФЕРА: Сферическая гармоническая упругая регистрация данных HARDI». NeuroImage. 55 (2): 545–556. Дои:10.1016 / j.neuroimage.2010.12.015. ЧВК 3035740. PMID 21147231.
- ^ П Чжан; М. Нитхаммер; Д Шен; Пи-Т Яп (2012). «Диффеоморфная регистрация диффузно-взвешенных изображений при больших деформациях» (PDF). Труды по обработке медицинских изображений и компьютерному вмешательству (MICCAI). Дои:10.1007/978-3-642-33418-4_22.
- ^ M Descoteaux; Р. Дериче (сентябрь 2007 г.). «Сегментация изображений Q-Ball с использованием статистической эволюции поверхности». Труды по обработке медицинских изображений и компьютерному вмешательству (MICCAI) 2007, LNCS 4792. С. 769–776. Дои:10.1007/978-3-540-75759-7_93.
- ^ а б Friston, K .; Холмс, А .; Worsley, K .; Poline, J .; Frith, C .; Frackowiak, R .; и другие. (1995). «Статистические параметрические карты в функциональной визуализации: общий линейный подход». Hum Brain Mapp. 2 (4): 189–210. Дои:10.1002 / hbm.460020402.
- ^ Buckner, R.L .; Andrews-Hanna, J. R .; Шактер, Д. Л. (2008). «Сеть мозга по умолчанию: анатомия, функции и отношение к болезни». Летопись Нью-Йоркской академии наук. 1124 (1): 1–38. Bibcode:2008НЯСА1124 .... 1Б. CiteSeerX 10.1.1.689.6903. Дои:10.1196 / летопись.1440.011. PMID 18400922.
- ^ а б Йео, Б. Т. Т .; Krienen, F.M .; Sepulcre, J .; Sabuncu, M. R .; Лашкари, Д .; Hollinshead, M .; Roffman, J. L .; Smoller, J. W .; Zöllei, L .; Polimeni, J. R .; Fischl, B .; Liu, H .; Бакнер, Р. Л. (2011). «Организация коры головного мозга человека оценивается по внутренним функциональным связям». J Нейрофизиол. 106 (3): 1125–65. Дои:10.1152 / ян.00338.2011. ЧВК 3174820. PMID 21653723.
- ^ Дж. В. Хэксби; М. И. Гоббини; М. Л. Фьюри; А. Ишай; Дж. Л. Схоутен; П. Пьетрини (2001). «Распределенные и перекрывающиеся изображения лиц и предметов в вентральной височной коре». Наука. 293 (5539): 2425–30. Bibcode:2001Sci ... 293.2425H. CiteSeerX 10.1.1.381.2660. Дои:10.1126 / science.1063736. PMID 11577229.
- ^ Langs, G .; Menze, B.H .; Лашкари, Д .; Голланд, П. (2011). «Обнаружение стабильных распределенных паттернов активации мозга с помощью контраста Джини». NeuroImage. 56 (2): 497–507. Дои:10.1016 / j.neuroimage.2010.07.074. ЧВК 3960973. PMID 20709176.
- ^ Varoquaux, G .; Грамфорт, А .; Pedregosa, F .; Michel, V .; Тирион, Б. (2011). «Обучение многопредметному словарю для сегментирования атласа спонтанной активности мозга». Inf Process Med Imaging. 22. С. 562–73.
- ^ van den Heuvel, M. P .; Stam, C.J .; Kahn, R. S .; Хулсхоф Пол, Х. Э. (2009). «Эффективность функциональных сетей мозга и интеллектуальная производительность». J Neurosci. 29 (23): 7619–24. Дои:10.1523 / JNEUROSCI.1443-09.2009. ЧВК 6665421. PMID 19515930.
- ^ Фристон, К. (2003). «Динамическое причинно-следственное моделирование». NeuroImage. 19 (4): 1273–1302. Дои:10.1016 / S1053-8119 (03) 00202-7. PMID 12948688.
- ^ Sabuncu, M. R .; Зингер Б.Д .; Conroy, B .; Bryan, R.E .; Ramadge, P.J .; Хэксби, Дж. В. (2010). «Функциональное межпредметное выравнивание кортикальной анатомии человека». Кора головного мозга. 20 (1): 130–140. Дои:10.1093 / cercor / bhp085. ЧВК 2792192. PMID 19420007.
- ^ Langs, G .; Лашкари, Д .; Sweet, A .; Галстук, Y .; Риголо, Л .; Golby, A.J .; Голланд, П. (2011). «Изучение атласа познавательного процесса в его функциональной геометрии». Inf Process Med Imaging. 22. С. 135–46.
- ^ Haxby, J. V .; Guntupalli, J. S .; Connolly, A.C .; Гальченко Ю.О .; Conroy, B.R .; Gobbini, M. I .; Hanke, M .; Рамадж, П. Дж. (2011). «Общая многомерная модель репрезентативного пространства вентральной височной коры человека». Нейрон. 72 (2): 404–416. Дои:10.1016 / j.neuron.2011.08.026. ЧВК 3201764. PMID 22017997.
- ^ Уэллс, Уильям М; Колчестер, Алан; Делп, Скотт (1998). Конспект лекций по информатике (Представлена рукопись). Конспект лекций по информатике. 1496. Дои:10.1007 / BFb0056181. ISBN 978-3-540-65136-9.
- ^ Дж. С. Дункан; Н Аяче (2000). «Медицинский анализ изображений: прогресс за два десятилетия и предстоящие задачи». IEEE Transactions по анализу шаблонов и машинному анализу. 22: 85–106. CiteSeerX 10.1.1.410.8744. Дои:10.1109/34.824822.
Журналы по медицинской обработке изображений
- Анализ медицинских изображений (MedIA) ; также официальный журнал Общество MICCAI, который организует Ежегодная конференция MICCAI ведущая конференция по медицинской обработке изображений
- IEEE Transactions on Medical Imaging (IEEE TMI)
- Медицинская физика
- Журнал цифровой обработки изображений (JDI) ; официальный журнал Общество информатики изображений
- Компьютеризированная медицинская визуализация и графика
- Журнал компьютерной радиологии и хирургии
- BMC Medical Imaging
Кроме того, следующие журналы иногда публикуют статьи, описывающие методы и конкретные клинические применения вычислений медицинских изображений или обработки медицинских изображений, специфичных для конкретных методов.