WikiDer > Микроканонический ансамбль

Статистическая механика
Термодинамика Кинетическая теория
Статистика частиц Теорема спин-статистики Идентичные частицы Максвелл – Больцманн Бозе-Эйнштейн Ферми – Дирак Парастатистика Статистика Anyonic Статистика плетения
Термодинамические ансамбли NVE Микроканонический NVT Канонический мкВт Большой канонический НПХ Изоэнтальпийно-изобарический ДНЯО Изотермически-изобарический
Модели Дебай Эйнштейн Я пою Potts
Потенциал Внутренняя энергия Энтальпия Свободная энергия Гельмгольца Свободная энергия Гиббса Большой потенциал / свободная энергия Ландау
Ученые Максвелл Больцман Гиббс Эйнштейн Эренфест фон Нейман Толман Дебай Ферми Bose
v т е

В статистическая механика, а микроканонический ансамбль это статистический ансамбль который используется для представления возможных состояний механической системы, которая имеет точно заданную полную энергию.^[1] Предполагается, что система изолирована в том смысле, что система не может обмениваться энергией или частицами с окружающей средой, так что (по сохранение энергии) энергия системы остается неизменной с течением времени. Энергия, состав, объем и форма системы остаются неизменными во всех возможных состояниях системы.

Макроскопические переменные микроканонического ансамбля - это величины, которые влияют на природу микросостояний системы, такие как общее количество частиц в системе (символ: N), объем системы (символ: V), а также полную энергию в системе (символ: E). Поэтому этот ансамбль иногда называют NVE ансамбль, поскольку каждая из этих трех величин является константой ансамбля.

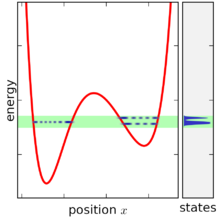
Проще говоря, микроканонический ансамбль определяется путем присвоения равной вероятности каждому микрогосударство чья энергия попадает в диапазон с центром в E. Всем остальным микросостояниям присваивается нулевая вероятность. Так как вероятности должны составлять в сумме 1, вероятность п является обратной величиной числа микросостояний W в диапазоне энергий,

${ displaystyle P = 1 / W,}$

Затем диапазон энергии уменьшается по ширине, пока не станет равным. бесконечно мало узкий, все еще в центре E. в предел В результате этого процесса получается микроканонический ансамбль.^[1]

Применимость

Микроканонический ансамбль иногда считают фундаментальное распределение статистической термодинамики, поскольку ее форма может быть обоснована элементарными основаниями, такими как принцип безразличия: микроканонический ансамбль описывает возможные состояния изолированной механической системы, когда энергия известна точно, но без дополнительной информации о внутреннем состоянии. Кроме того, в некоторых специальных системах эволюция эргодический в этом случае микроканонический ансамбль равен ансамблю времени, когда начинается с одного состояния энергии. E (временной ансамбль - это ансамбль, состоящий из всех будущих состояний, возникших из одного начального состояния).

На практике микроканонический ансамбль не соответствует экспериментально реалистичной ситуации. В реальной физической системе есть, по крайней мере, некоторая неопределенность в отношении энергии из-за неконтролируемых факторов при подготовке системы. Помимо трудности поиска экспериментального аналога, трудно проводить расчеты, которые точно удовлетворяют требованию фиксированной энергии, поскольку это препятствует отдельному анализу логически независимых частей системы. Более того, существуют неясности в отношении подходящих определений таких величин, как энтропия и температура, в микроканоническом ансамбле.^[1]

Системы, находящиеся в тепловом равновесии с окружающей средой, имеют неопределенность по энергии и вместо этого описываются канонический ансамбль или большой канонический ансамбль, последнее, если система также находится в равновесии со своим окружением в отношении обмена частицами.

Характеристики

Термодинамические аналогии

Ранние работы в статистической механике Людвиг Больцманн привел к его одноименное уравнение энтропии для системы с заданной полной энергией, S = k бревно W, куда W - это количество различных состояний, доступных для системы при этой энергии. Больцман не стал вдаваться в подробности о том, что именно составляет набор различных состояний системы, помимо частного случая идеального газа. Эта тема была исследована до конца Джозайя Уиллард Гиббс который разработал обобщенную статистическую механику для произвольных механических систем и определил микроканонический ансамбль, описанный в этой статье.^[1] Гиббс тщательно исследовал аналогии между микроканоническим ансамблем и термодинамикой, особенно то, как они разрушаются в случае систем с несколькими степенями свободы. Он ввел еще два определения микроканонической энтропии, которые не зависят от ω - описанные выше объемная и поверхностная энтропия. (Отметим, что поверхностная энтропия отличается от энтропии Больцмана только на величину ω-зависимое смещение.)

Объемная энтропия S_v и связанные Т_v образуют близкую аналогию с термодинамической энтропией и температурой. Можно точно показать, что

${ displaystyle dE = T _ { rm {v}} dS _ { rm {v}} - langle P rangle dV,}$

(⟨п⟩ - среднее давление по ансамблю), как и ожидалось для первый закон термодинамики. Аналогичное уравнение можно найти для поверхностной (больцмановской) энтропии и связанной с ней Т_sоднако «давление» в этом уравнении - сложная величина, не связанная со средним давлением.^[1]

Микроканонический Т_v и Т_s не вполне удовлетворительны по аналогии с температурой. Вне термодинамический предел, возникает ряд артефактов.

• Нетривиальный результат объединения двух систем: Две системы, каждая из которых описывается независимым микроканоническим ансамблем, могут быть приведены в тепловой контакт и уравновешены в комбинированную систему, также описываемую микроканоническим ансамблем. К сожалению, поток энергии между двумя системами невозможно предсказать на основе начального Тс. Даже когда первоначальный Травны, может передаваться энергия. Более того, Т комбинации отличается от начальных значений. Это противоречит интуиции, что температура должна быть большой величиной и что две системы с одинаковой температурой не должны подвергаться воздействию теплового контакта.^[1]
• Странное поведение для систем с несколькими частицами: Многие результаты, например микроканонические Теорема о равнораспределении получить смещение с одной или двумя степенями свободы при записи в терминах Т_s. Для небольших систем это смещение является значительным, поэтому, если мы сделаем S_s Аналог энтропии, необходимо сделать несколько исключений для систем только с одной или двумя степенями свободы.^[1]
• Ложные отрицательные температуры: Отрицательный Т_s возникает всякий раз, когда плотность состояний убывает с энергией. В некоторых системах плотность состояний не монотонный в энергии, и так Т_s может менять знак несколько раз при увеличении энергии.^[4][5]

Предпочтительное решение этих проблем - избегать использования микроканонического ансамбля. Во многих реальных случаях система термостатируется термостатом, так что энергия точно не известна. Тогда более точное описание - это канонический ансамбль или же большой канонический ансамбль, оба из которых полностью соответствуют термодинамике.^[6]

Точные выражения для ансамбля

Точное математическое выражение для статистического ансамбля зависит от типа рассматриваемой механики - квантовой или классической, - поскольку понятие «микросостояние» в этих двух случаях существенно различается. В квантовой механике диагонализация предоставляет дискретный набор микрогосударства с определенными энергиями. В классическом механическом случае вместо этого используется интеграл по каноническому фазовое пространство, а размер микросостояний в фазовом пространстве может быть выбран несколько произвольно.

Чтобы построить микроканонический ансамбль, в обоих типах механики необходимо сначала указать диапазон энергии. В выражениях ниже функция ${ displaystyle f ({ tfrac {H-E} { omega}})}$ (функция ЧАС, достигая максимума E с шириной ω) будет использоваться для представления диапазона энергий, в который включаются состояния. Примером этой функции может быть^[1]

${ displaystyle f (x) = { begin {cases} 1, & mathrm {if} ~ | x | <{ tfrac {1} {2}}, 0, & mathrm {в противном случае.} конец {case}}}$

или, более плавно,

${ Displaystyle f (x) = e ^ {- pi x ^ {2}}.}$

Квантовая механика

Пример микроканонического ансамбля для квантовой системы, состоящей из одной частицы в потенциальной яме.

График всех возможных состояний этой системы. Доступные стационарные состояния отображаются в виде горизонтальных полос различной темноты в зависимости от |ψ_я(х) |².

Ансамбль, содержащий только те состояния в узком интервале энергий. Когда энергетическая ширина равна нулю, получается микроканонический ансамбль (при условии, что интервал содержит хотя бы одно состояние).

Гамильтониан частицы равен Шредингер-тип, ЧАС = U(Икс) + п²/2м (потенциал U(Икс) изображена красной кривой). На каждой панели показан график энергетического положения с различными стационарными состояниями, а также боковой график, показывающий распределение состояний по энергии.

Статистический ансамбль в квантовой механике представлен матрица плотности, обозначаемый ${ displaystyle { hat { rho}}}$. Микроканонический ансамбль можно записать с помощью обозначение бюстгальтера, с точки зрения системы собственные состояния энергии и собственные значения энергии. Учитывая полный базис собственных состояний энергии |ψ_я⟩, проиндексировано я, микроканонический ансамбль^{[нужна цитата]}

${ displaystyle { hat { rho}} = { frac {1} {W}} sum _ {i} f left ({ tfrac {H_ {i} -E} { omega}} right ) | psi _ {i} rangle langle psi _ {i} |,}$

где ЧАС_я - собственные значения энергии, определяемые ${ displaystyle { hat {H}} | psi _ {i} rangle = H_ {i} | psi _ {i} rangle}$ (здесь ЧАС - оператор полной энергии системы, т.е. е., Гамильтонов оператор). Значение W определяется требованием, чтобы ${ displaystyle { hat { rho}}}$ является нормализованной матрицей плотности, поэтому

${ displaystyle W = sum _ {i} f left ({ tfrac {H_ {i} -E} { omega}} right).}$

Функция государственного объема (используемая для вычисления энтропии) определяется выражением

${ displaystyle v (E) = sum _ {H_ {i}$

Микроканонический ансамбль определяется путем принятия предела матрицы плотности, когда ширина энергии стремится к нулю, однако проблемная ситуация возникает, когда ширина энергии становится меньше, чем расстояние между уровнями энергии. При очень малой энергетической ширине ансамбль вообще не существует для большинства значений E, так как никакие состояния не попадают в диапазон. Когда ансамбль действительно существует, он обычно содержит только один (или два) состояний, так как в сложной системе уровни энергии всегда равны только случайно (см. теория случайных матриц для более подробного обсуждения этого вопроса). Более того, функция объема состояний также увеличивается только дискретными приращениями, и поэтому ее производная всегда бесконечна или равна нулю, что затрудняет определение плотности состояний. Эта проблема может быть решена путем отказа от полного доведения диапазона энергий до нуля и сглаживания функции состояния-объема, однако это усложняет определение ансамбля, так как в этом случае становится необходимым указать диапазон энергий в дополнение к другим переменным (вместе , NVEω ансамбль).

Классическая механика

Пример микроканонического ансамбля для классической системы, состоящей из одной частицы в потенциальной яме.

График всех возможных состояний этой системы. Доступные физические состояния равномерно распределены в фазовом пространстве, но с неравномерным распределением энергии; боковой график отображает dv/dE.

Ансамбль, ограниченный только этими состояниями в узком интервале энергий. Этот ансамбль выглядит как тонкая оболочка в фазовом пространстве. Когда энергетическая ширина равна нулю, получается микроканонический ансамбль.

Каждая панель показывает фазовое пространство (верхний график) и пространство энергетических позиций (нижний график). Гамильтониан частицы равен ЧАС = U(Икс) + п²/2м, с потенциалом U(Икс) показан красной кривой. На боковом графике показано распределение состояний по энергии.

В классической механике ансамбль представлен совместная функция плотности вероятности ρ(п₁, … п_п, q₁, … q_п) определяется над системой фазовое пространство.^[1] Фазовое пространство имеет п обобщенные координаты называется q₁, … q_п, и п связанный канонические импульсы называется п₁, … п_п.

Функция плотности вероятности для микроканонического ансамбля:

${ displaystyle rho = { frac {1} {h ^ {n} C}} { frac {1} {W}} f ({ tfrac {H-E} { omega}}),}$

куда

• ЧАС полная энергия (Гамильтониан) системы, функция фазы (п₁, … q_п),
• час - произвольная, но заранее определенная константа с единицами измерения энергия × время, устанавливая размер одного микрогосударства и обеспечивая правильные размеры для ρ.^{[заметка 2]}
• C - это поправочный коэффициент для пересчета, часто используемый для систем частиц, в которых идентичные частицы могут меняться местами друг с другом.^{[заметка 3]}

Опять же, значение W определяется требованием, чтобы ρ - нормированная функция плотности вероятности:

${ displaystyle W = int ldots int { frac {1} {h ^ {n} C}} f ({ tfrac {HE} { omega}}) , dp_ {1} ldots dq_ { n}}$

Этот интеграл берется по всей фазовое пространство. Функция государственного объема (используемая для вычисления энтропии) определяется как

${ displaystyle v (E) = int ldots int _ {H$

Поскольку ширина энергии ω принимается равным нулю, значение W уменьшается пропорционально ω в качестве W = ω (dv/dE).

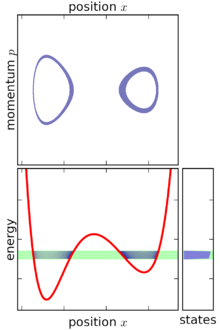
Основываясь на приведенном выше определении, микроканонический ансамбль можно представить как бесконечно тонкую оболочку в фазовом пространстве с центром на поверхности с постоянной энергией. Хотя микроканонический ансамбль ограничен этой поверхностью, он не обязательно равномерно распределен по этой поверхности: если градиент энергии в фазовом пространстве меняется, то микроканонический ансамбль «толще» (более концентрирован) в некоторых частях поверхность, чем другие. Эта особенность является неизбежным следствием требования, чтобы микроканонический ансамбль был стационарным.

Совершенная энтропия газа и термодинамический предел

Воспользуемся микроканоническим описанием для характеристики идеального газа, состоящего из N точечных частиц в объеме V, массы m и пустотного спина. Изолированный газ имеет полную энергию ${ displaystyle E pm dE}$. Напоминаем, что энергия частицы определяется количественно: ${ displaystyle E = { frac { hbar ^ {2} k ^ {2}} {2m}}, k_ {i} = n_ {i} { frac {2 pi} {L_ {i}}} ~ n_ {i} in mathbb {Z}}$. Прежде всего, мы должны определить номер вектора, имеющего норму типа ${ displaystyle { frac { hbar ^ {2} k ^ {2}} {2m}} leq E iff k ^ {2} leq { frac {2mE} { hbar ^ {2}}} }$ при соблюдении дискретности ${ displaystyle k}$.

Таким образом, функция фазового объема v(E) можно рассматривать как количество элементарных сеток, которые мы можем поместить в сферу радиуса ${ displaystyle { sqrt { frac {2mE} { hbar}}}}$. Для газа N частиц размер k равен 3N, тогда элементарная сетка представляет собой гиперкуб объема ${ displaystyle (k_ {x} k_ {y} k_ {z}) ^ {N} = { frac {V ^ {N}} {(2 pi) ^ {3N}}}}$ и (3N-гипер) сфера радиуса ${ displaystyle { sqrt { frac {2mE} { hbar}}}}$ имеет объем ${ displaystyle { frac { pi ^ { frac {3N} {2}}} { Gamma ({ frac {3N} {2}} + 1)}} left ({ sqrt { frac { 2mE} { hbar}}} right) ^ {3N}}$, куда ${ Displaystyle Gamma (х)}$ это гамма-функция.

Следовательно, ${ displaystyle v (E) = { frac {{ mbox {Объем гиперсферы радиуса}} { sqrt { frac {2mE} { hbar}}}} { mbox {Объем элементарной сетки} }}}$

Для определения энтропии мы должны выразить ${ displaystyle { frac {dv} {dE}} = { frac {V ^ {N}} {(2 pi) ^ {3N}}} ({ frac {2m} { hbar ^ {2} }}) ^ { frac {3N} {2}} { frac { pi ^ { frac {3N} {2}}} { Gamma ({ frac {3N} {2}} + 1)} } { frac {3N} {2}} E ^ {{ frac {3N} {2}} - 1}}$

Поскольку частицы неразличимы, мы делим количество возможных состояний на N! в рамках приближения Максвелла-Больцмана.

Тогда энтропия равна: ${ Displaystyle S = к ~ журнал left ({ frac {dv} {dE}} right) = kN left (журнал left ({ frac {V} {N}} right) + { frac {3} {2}} журнал left ({ frac {mE} {3 pi hbar ^ {2} N}} right) + { frac {5} {2}} right)}$, где мы использовали приближение Стирлинга с ${ displaystyle N gg 1}$, наконец, мы находим Уравнение Сакура – ​​Тетрода.

Мы легко находим микроканонические температуры ${ displaystyle { frac {1} {T}} = { frac { partial S} { partial E}} = { frac {3} {2}} { frac {N} {E}} к iff E = { frac {3} {2}} кНТ}$, находим хорошо известный результат Кинетическая теория газов.

Кроме того, мы находим знаменитые закон идеального газадействительно у нас есть ${ displaystyle { frac {p} {T}} = { frac { partial S} { partial V}} = { frac {kN} {V}} iff pV = NkT}$

Примечания

Рекомендации