WikiDer > Пятиугольный двустворчатый
| Пятиугольный двустворчатый | |
|---|---|
 | |
| Тип | Bifrustum |
| Лица | 10 трапеции, 2 пятиугольники |
| Края | 20 |
| Вершины | 15 |
| Группа симметрии | D5ч |
| Двойной многогранник | удлиненная пятиугольная дипирамида |
| Характеристики | выпуклый |
Сеть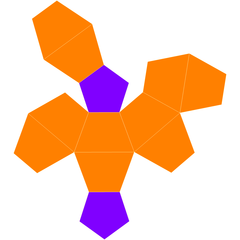 | |
В пятиугольный двустворчатый или же усеченный пятиугольник бипирамида является третьим в бесконечной серии двустворчатый многогранники. Имеет 10 трапеция и 2 пятиугольник лица.
Конструкции
Пятиугольное двустворчатое дерево - это двойственный многогранник из Джонсон солид, то удлиненная пятиугольная бипирамида. А Джонсон солид один из 92 строго выпуклый многогранники который состоит из правильный многоугольник лица, но не униформа многогранники (т. е. не Платоновы тела, Архимедовы тела, призмы, или же антипризмы). Их назвали Норман Джонсон, которые впервые перечислили эти многогранники в 1966 году.[1]
Этот многогранник можно построить, взяв пятиугольная бипирамида и усечение вершин полярной оси. В Конвейв обозначении многогранников, он может быть представлен как многогранник "t5dP5", что означает усечение вершин пятой степени двойственного к пятиугольная призма.[2]
Как вариант, его можно построить, склеив два встык пятиугольных усикиили (если допускаются компланарные грани) склейкой двух пятиугольных призм на их пятиугольных гранях.
Заявление
В формировании квазикристаллы, структура усеченной пентагональной бипирамиды с 15 сайтами может образовывать ядро более крупных структур с пятикратной или икосаэдрической симметрией.[3]
Рекомендации
- ^ Джонсон, Норман В. (1966), «Выпуклые многогранники с правильными гранями», Канадский математический журнал, 18: 169–200, Дои:10.4153 / cjm-1966-021-8, МИСТЕР 0185507, Zbl 0132.14603.
- ^ Обозначение Конвея для многогранников, Джордж У. Харт, дата обращения 20 декабря 2014.
- ^ Хофмайстер, Герберт (1999), «Пятикратное двойникование в наноразмерных частицах и нанокристаллических тонких пленках - повсеместные метастабильные структуры» (PDF), Форум материаловедения, 312–314: 325–332, Дои:10.4028 / www.scientific.net / MSF.312-314.325, S2CID 136620837.