WikiDer > Пентакис икосододекаэдр
| Пентакис икосододекаэдр | |
|---|---|
 | |
| Геодезический многогранник | (2,0) |
| Обозначение Конвея | k5aD = dcD = uI |
| Лица | 80 треугольники (20 равносторонний; 60 равнобедренных) |
| Края | 120 (2 типа) |
| Вершины | 42 (2 типа) |
| Конфигурации вершин | (12) 35 (30) 36 |
| Группа симметрии | Икосаэдр (ячас) |
| Двойной многогранник | Додекаэдр с фаской |
| Характеристики | выпуклый |
 Сеть | |
В пентакис икосододекаэдр или разделенный икосаэдр это выпуклый многогранник с 80 треугольными лица, 120 края, и 42 вершины. Это двойник усеченный ромбический триаконтаэдр (додекаэдр с фаской).
строительство
Его название происходит от топологической конструкции из икосододекаэдр с kis оператор применяется к пятиугольным граням. В этой конструкции предполагается, что все вершины находятся на одинаковом расстоянии от центра, в то время как в целом симметрия икосаэдра может поддерживаться даже с вершинами 12 порядка 5 на другом расстоянии от центра, чем остальные 30.
Его также можно топологически построить из икосаэдр, разделив каждую треугольную грань на 4 треугольника, добавив вершины среднего ребра. В этой конструкции все 80 треугольников будут равносторонними, а грани - равносторонними. копланарный.
| Конвей | (ты2)Я | (k5) aI |
|---|---|---|
| Изображение |  | 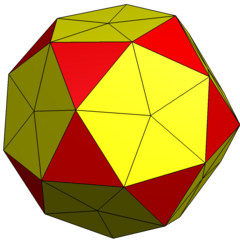 |
| Форма | 2-частотные разделенные икосаэдр | Пентакис икосододекаэдр |
Связанные многогранники
Додекаэдр пентакиса немного меньше Каталонский твердый который имеет 60 граней равнобедренного треугольника, 90 ребер (2 типа) и 32 вершины (2 типа).
Трипентакис икосододекаэдр, Kleetope икосододекаэдра, можно получить, подняв низкие пирамиды на каждой равносторонней треугольной грани пентакисикосододекаэдра. Он имеет 120 граней равнобедренного треугольника (2 типа), 180 ребер (3 типа) и 62 вершины (3 типа).
Невыпуклый малый икосигемидодекаэдр выглядит как пентакис икосододекаэдр с перевернутым пятиугольные пирамиды встреча в центре многогранника.
Связанные фрукты
Он представляет собой внешнюю оболочку вершинно-центрированного ортогональная проекция из 600 ячеек, один из шести выпуклые правильные 4-многогранники, в 3 измерениях.
Смотрите также
Рекомендации
- Джордж У. Харт, Скульптура на основе пропеллоризированных многогранников, Proceedings of MOSAIC 2000, Сиэтл, Вашингтон, август 2000 г., стр. 61–70. [1]
- Джон Х. Конвей, Хайди Берджель, Хаим Гудман-Штрасс, Симметрии вещей 2008, ISBN 978-1-56881-220-5
- Глава 21.Название архимедовых и каталонских многогранников и плиток (стр.284)
- Веннингер, Магнус (1979), Сферические модели, Издательство Кембриджского университета, ISBN 978-0-521-29432-4, Г-Н 0552023 Дувр 1999 ISBN 978-0-486-40921-4
внешняя ссылка
- Многогранный генератор VTML Попробуйте "k5aD" (Обозначения многогранника Конвея)



