WikiDer > Радиус схождения
В математика, то радиус схождения из степенной ряд это радиус наибольшего диск в которой серии сходится. Это либо неотрицательное действительное число, либо . Когда он положительный, степенной ряд сходится абсолютно и равномерно на компактах внутри открытого диска радиуса, равного радиусу схождения, и это Серия Тейлор из аналитическая функция к которому он сходится.
Определение
Для степенного ряда ƒ определяется как:
куда,
- а это сложный константа, центр диск конвергенции,
- cп это пth комплексный коэффициент, и
- z - комплексная переменная.
Радиус схождения р неотрицательное действительное число или такой, что ряд сходится, если
и расходится, если
Некоторые могут предпочесть альтернативное определение, поскольку существование очевидно:
На границе, то есть где |z − а| = р, поведение степенного ряда может быть сложным, и ряд может сходиться для некоторых значений z и расходятся для других. Радиус сходимости бесконечен, если ряд сходится при всех сложные числа z.[1]
Нахождение радиуса сходимости
Возникают два случая. Первый случай теоретический: когда известны все коэффициенты затем вы берете определенные пределы и находите точный радиус конвергенции. Второй случай является практическим: когда вы строите решение сложной задачи в виде степенного ряда, вы обычно будете знать только конечное число членов в степенном ряду, от пары до ста членов. Во втором случае экстраполяция графика позволяет оценить радиус сходимости.
Теоретический радиус
Радиус сходимости можно найти, применив корневой тест к условиям сериала. Корневой тест использует число
"lim sup" означает предел высшего. Корневой тест утверждает, что ряд сходится, если C <1 и расходится, еслиC > 1. Отсюда следует, что степенной ряд сходится, если расстояние от z в центр а меньше чем
и расходится, если расстояние превышает это число; это заявление является Теорема Коши – Адамара. Обратите внимание, что р = 1/0 интерпретируется как бесконечный радиус, что означает, что ƒ является вся функция.
Предел, связанный с тест соотношения обычно легче вычислить, и когда этот предел существует, он показывает, что радиус сходимости конечен.
Это показано следующим образом. Тест отношения говорит, что ряд сходится, если
Это эквивалентно
Практическая оценка радиуса в случае реальных коэффициентов
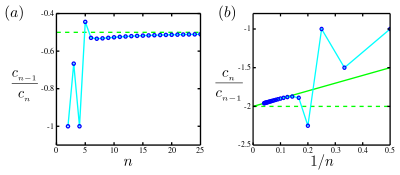
Обычно в научных приложениях только конечное число коэффициентов известны. Обычно[нечеткий] в качестве возрастает, эти коэффициенты принимают регулярное поведение, определяемое ближайшей сингулярностью, ограничивающей радиус. В этом случае были разработаны два основных метода, основанных на том факте, что коэффициенты ряда Тейлора примерно экспоненциальны с отношением где r - радиус сходимости.
- Основной случай - это когда коэффициенты в конечном итоге имеют общий знак или чередуются по знаку. Как указывалось ранее в статье, во многих случаях предел существует, и в этом случае Отрицательный означает, что сингулярность, ограничивающая сходимость, находится на отрицательной оси. Оцените этот предел, построив график против , и графически экстраполировать на (эффективно ) посредством линейной подгонки. Перехват с оценивает обратную величину радиуса сходимости, . Этот сюжет называется Заговор Домба – Сайкса.
- Более сложный случай, когда знаки коэффициентов имеют более сложный узор. Мерсер и Робертс предложили следующую процедуру.[3] Определите связанную последовательность
- Постройте конечное число известных против , и графически экстраполировать на через линейную посадку. Перехват с оценивает обратную величину радиуса сходимости, .
- Эта процедура также оценивает две другие характеристики особенности, предельной сходимости. Предположим, что ближайшая особенность имеет степень и имеет угол к реальной оси. Тогда наклон приведенной выше линейной аппроксимации равен . Далее сюжет против , то линейная аппроксимация экстраполирована на перехватил .
Радиус сходимости в комплексном анализе
Степенный ряд с положительным радиусом сходимости может быть преобразован в голоморфная функция приняв его аргумент как сложную переменную. Радиус сходимости можно охарактеризовать следующей теоремой:
- Радиус сходимости степенного ряда ƒ сосредоточен на точке а равно расстоянию от а до ближайшей точки где ƒ не может быть определен таким образом, чтобы сделать его голоморфным.
Множество всех точек, расстояние до которых а строго меньше радиуса сходимости называется диск схождения.
Ближайшая точка означает ближайшую точку в комплексная плоскость, не обязательно на реальной линии, даже если центр и все коэффициенты действительны. Например, функция
не имеет особенностей на прямой, так как не имеет настоящих корней. Его ряд Тейлора около 0 определяется выражением
Корневой тест показывает, что его радиус сходимости равен 1. В соответствии с этим функция ƒ(z) имеет особенности в ±я, которые находятся на расстоянии 1 от 0.
Для доказательства этой теоремы см. аналитичность голоморфных функций.
Простой пример
Функция арктангенса тригонометрия может быть расширен в степенной ряд:
В этом случае легко применить корневой тест, чтобы найти, что радиус сходимости равен 1.
Более сложный пример
Рассмотрим этот степенной ряд:
где рациональные числа Bп являются Числа Бернулли. Может оказаться обременительным попытаться применить тест отношения, чтобы найти радиус сходимости этого ряда. Но сформулированная выше теорема комплексного анализа быстро решает проблему. В z = 0, особенность фактически отсутствует, поскольку особенность устранима. Таким образом, единственные неизвлекаемые особенности расположены на Другой точки, где знаменатель равен нулю. Мы решаем
напоминая, что если z = Икс + иу и е иу = cos (у) + я грех (у) тогда
а затем взять Икс и у быть реальным. С у действительно, абсолютное значение cos (у) + я грех (у) обязательно равно 1. Следовательно, абсолютное значение е z может быть 1, только если е Икс равно 1; поскольку Икс реально, это происходит, только если Икс = 0. Следовательно z чисто мнимое и cos (у) + я грех (у) = 1. Поскольку у реально, это происходит, только если cos (у) = 1 и sin (у) = 0, так что у целое число, кратное 2π. Следовательно, особые точки этой функции находятся в точках
- z = ненулевое целое число, кратное 2πя.
Ближайшие к 0 особенности, являющиеся центром разложения в степенной ряд, находятся на уровне ± 2πя. Расстояние от центра до любой из этих точек равно 2π, поэтому радиус сходимости равен 2π.
Сходимость на границе
Если степенной ряд расширен вокруг точки а а радиус сходимости равен р, то множество всех точек z такой, что |z − а| = р это круг называется граница диска схождения. Степенный ряд может расходиться в каждой точке границы или расходиться в одних точках и сходиться в других точках или сходиться во всех точках границы. Более того, даже если ряд сходится всюду на границе (даже равномерно), он не обязательно сходится абсолютно.
Пример 1: степенной ряд для функции ƒ(z) = 1/(1 − z), расширился вокруг z = 0, что просто
имеет радиус сходимости 1 и расходится в каждой точке границы.
Пример 2: степенной ряд для грамм(z) = −ln (1 - z), расширился вокруг z = 0, который
имеет радиус сходимости 1 и расходится при z = 1 но сходится для всех остальных точек на границе. Функция ƒ(z) примера 1 - это производная из грамм(z).
Пример 3: степенной ряд
имеет радиус сходимости 1 и абсолютно сходится всюду на границе. Если час - функция, представленная этим рядом на единичном круге, то производная от час(z) равно грамм(z)/z с грамм примера 2. Оказывается, что час(z) это дилогарифм функция.
Пример 4: степенной ряд
имеет радиус сходимости 1 и сходится равномерно на всей границе |z| = 1, но не сходятся абсолютно на границе.[4]
Скорость сходимости
Если мы расширим функцию
вокруг точки Икс = 0, получаем, что радиус сходимости этого ряда равен означает, что этот ряд сходится для всех комплексных чисел. Однако в приложениях часто интересует точность числовой ответ. И количество членов, и значение, по которому должна оцениваться серия, влияют на точность ответа. Например, если мы хотим вычислить ж(0,1) = грех (0,1) с точностью до пяти десятичных знаков, нам нужны только первые два члена ряда. Однако, если нам нужна такая же точность для Икс = 1 мы должны оценить и суммировать первые пять членов ряда. За ж(10), требуются первые 18 членов ряда, а для ж(100) нам нужно оценить первые 141 член.
Таким образом, для этих конкретных значений самая быстрая сходимость разложения степенного ряда находится в центре, а по мере удаления от центра сходимости скорость сходимости замедляется, пока вы не достигнете границы (если она существует) и не пересечете ее, и в этом случае серии будут расходиться.
Абсцисса сходимости ряда Дирихле.
Аналогичным понятием является абсцисса схождения Серия Дирихле
Такой ряд сходится, если действительная часть s больше определенного числа в зависимости от коэффициентов ап: the абсцисса конвергенции.
Примечания
- ^ Математический анализ-II. Кришна Пракашан СМИ. 16 ноября 2010 г.
- ^ См. Рисунок 8.1 в: Хинч, Э.Дж. (1991), Методы возмущений, Кембриджские тексты по прикладной математике, 6, Cambridge University Press, стр. 146, ISBN 0-521-37897-4
- ^ Mercer, G.N .; Робертс, А.Дж. (1990), "Описание центрального многообразия рассеивания загрязняющих веществ в каналах с различными свойствами потока", SIAM J. Appl. Математика., 50 (6): 1547–1565, Дои:10.1137/0150091
- ^ Серпинский, Вацлав (1918), "O szeregu potęgowym który jest zbieżny na całem swem kole zbieżności jednostajnie ale nie bezwzględnie", Праче Математика-физика, 29, стр. 263–266
Рекомендации
- Браун, Джеймс; Черчилль, Руэль (1989), Сложные переменные и приложения, Нью-Йорк: Макгроу-Хилл, ISBN 978-0-07-010905-6
- Штейн, Элиас; Шакарчи, Рами (2003), Комплексный анализ, Принстон, Нью-Джерси: Princeton University Press, ISBN 0-691-11385-8






![C = limsup_ {n rightarrow infty} sqrt [n] {| c_n (z-a) ^ n |} = limsup_ {n rightarrow infty} sqrt [n] {| c_n |} | z-a |](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b92c9c072ef7f2924a69f25573e57ae83bb9e54)
![r = frac {1} { limsup_ {n rightarrow infty} sqrt [n] {| c_n |}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b933707a8cf4a53585803d7236babf35708a83a)







































