В математика, а серии это сумма условий бесконечная последовательность номеров. Точнее, бесконечная последовательность  определяет серии S что обозначено
определяет серии S что обозначено

В пth частичная сумма Sп это сумма первых п условия последовательности; то есть,

Серия сходящийся (или же сходится) если последовательность  его частичных сумм стремится к предел; это означает, что при добавлении одного
его частичных сумм стремится к предел; это означает, что при добавлении одного  после другого в порядке, указанном индексами, получаются частичные суммы, которые становятся все ближе и ближе к заданному числу. Точнее, ряд сходится, если существует число
после другого в порядке, указанном индексами, получаются частичные суммы, которые становятся все ближе и ближе к заданному числу. Точнее, ряд сходится, если существует число  такое, что для любого сколь угодно малого положительного числа
такое, что для любого сколь угодно малого положительного числа  , существует (достаточно большой) целое число
, существует (достаточно большой) целое число  такой, что для всех
такой, что для всех  ,
,

Если ряд сходится, то (обязательно уникальное) число  называется сумма ряда.
называется сумма ряда.
То же обозначение

используется для ряда и, если он сходится, для его суммы. Это соглашение аналогично тому, которое используется для добавления: а + б обозначает операция добавления а и б а также результат этого добавление, который называется сумма из а и б.
Любой несходящийся ряд называется расходящийся или расходиться.
Примеры сходящихся и расходящихся рядов
- Обратные положительные целые числа произвести расходящийся ряд (гармонический ряд):

- Изменение знаков обратных положительных целых чисел дает сходящийся ряд (переменный гармонический ряд):

- Взаимные простые числа произвести расходящийся ряд (так что набор простых чисел "большой"; видеть расхождение суммы обратных простых чисел):

- Взаимные треугольные числа произвести сходящийся ряд:

- Взаимные факториалы производят сходящийся ряд (см. е):

- Взаимные квадратные числа производят сходящийся ряд ( Базельская проблема):

- Взаимные степени 2 производят сходящийся ряд (так что набор степеней двойки равен "маленький"):

- Взаимные степени любого n> 1 произвести сходящийся ряд:

- Чередование знаков взаимности степени 2 также производит сходящийся ряд:

- Меняя знаки обратных степеней любого n> 1, получаем сходящийся ряд:

- Взаимные Числа Фибоначчи производят сходящийся ряд (см. ψ):

Тесты сходимости
Существует несколько способов определить, сходится ли ряд или расходится.

Если синяя серия,

, можно доказать, что они сходятся, то меньший ряд

должны сходиться. Напротив, если красная серия

доказано, что расходится, то

тоже должны расходиться.
Сравнительный тест. Условия последовательности  сравниваются с таковыми из другой последовательности
сравниваются с таковыми из другой последовательности  . Если,
. Если,
для всех п,  , и
, и  сходится, то так же
сходится, то так же 
Однако если
для всех п,  , и
, и  расходится, значит, тоже
расходится, значит, тоже 
Соотношение тест. Предположим, что для всех п,  не равно нулю. Предположим, что существует
не равно нулю. Предположим, что существует  такой, что
такой, что

Если р <1, то ряд абсолютно сходится. Если р > 1, затем ряд расходится. Если р = 1, тест отношения не дает результатов, и ряды могут сходиться или расходиться.
Корневой тест или же пкорень th. Предположим, что члены рассматриваемой последовательности равны неотрицательный. Определять р следующее:
![r = limsup _ {n rightarrow infty} { sqrt [{n}] {| a_ {n} |}},](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd5eebb0f17b1155c0bea36edfdd50d6b9aa0f01)
- где "lim sup" обозначает предел высшего (возможно ∞; если предел существует, это то же значение).
Если р <1, то ряд сходится. Если р > 1, затем ряд расходится. Если р = 1, проверка корня неубедительна, и ряды могут сходиться или расходиться.
И тест соотношения, и тест корня основаны на сравнении с геометрическим рядом, и поэтому они работают в аналогичных ситуациях. Фактически, если тест соотношения работает (это означает, что предел существует и не равен 1), то также и корневой тест; обратное, однако, неверно. Таким образом, корневой тест применим более широко, но на практике предел часто бывает трудно вычислить для часто встречающихся типов рядов.
Интегральный тест. Ряд можно сравнить с интегралом, чтобы установить сходимость или расхождение. Позволять  быть позитивным и монотонно убывающая функция. Если
быть позитивным и монотонно убывающая функция. Если

тогда ряд сходится. Но если интеграл расходится, то расходится и ряд.
Предел сравнительного теста. Если  , а предел
, а предел  существует и не равно нулю, то
существует и не равно нулю, то  сходится если и только если
сходится если и только если  сходится.
сходится.
Испытание чередующейся серии. Также известен как Критерий Лейбница, то испытание с переменной последовательностью заявляет, что для чередующийся ряд формы  , если
, если  монотонно уменьшение, и имеет предел 0 на бесконечности, то ряд сходится.
монотонно уменьшение, и имеет предел 0 на бесконечности, то ряд сходится.
Тест конденсации Коши. Если  - положительная монотонно убывающая последовательность, то
- положительная монотонно убывающая последовательность, то сходится тогда и только тогда, когда
сходится тогда и только тогда, когда  сходится.
сходится.
Тест Дирихле
Тест Авеля
Условная и абсолютная сходимость

Иллюстрация абсолютной сходимости степенного ряда Exp [
z] около 0 оценивается в
z = Exp [я⁄3]. Длина линии конечна.
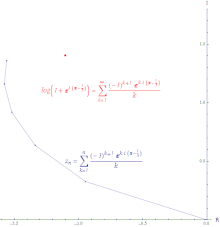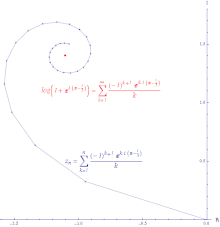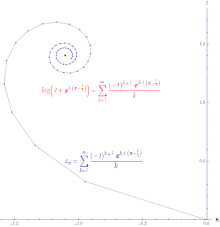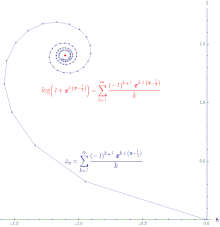
Иллюстрация условной сходимости степенного ряда log (
z+1) около 0 оценивается в
z = exp ((π−1⁄3)я). Длина линии бесконечна.
Для любой последовательности  ,
,  для всех п. Следовательно,
для всех п. Следовательно,

Это означает, что если  сходится, то
сходится, то  тоже сходится (но не наоборот).
тоже сходится (но не наоборот).
Если сериал  сходится, то ряд
сходится, то ряд  является абсолютно сходящийся. Абсолютно сходящаяся последовательность - это линия, в которой длина линии, созданной путем объединения всех приращений в частичную сумму, конечна. Силовой ряд экспоненциальная функция абсолютно везде сходится.
является абсолютно сходящийся. Абсолютно сходящаяся последовательность - это линия, в которой длина линии, созданной путем объединения всех приращений в частичную сумму, конечна. Силовой ряд экспоненциальная функция абсолютно везде сходится.
Если сериал  сходится, но ряд
сходится, но ряд  расходится, то серия
расходится, то серия  является условно сходящийся. Путь, образованный соединением частичных сумм условно сходящегося ряда, бесконечно велик. Силовой ряд логарифм условно сходится.
является условно сходящийся. Путь, образованный соединением частичных сумм условно сходящегося ряда, бесконечно велик. Силовой ряд логарифм условно сходится.
В Теорема рядов Римана утверждает, что если ряд сходится условно, можно переставить члены ряда таким образом, чтобы ряд сходился к любому значению или даже расходился.
Равномерная сходимость
Позволять  - последовательность функций. Сериал
- последовательность функций. Сериал  называется равномерно сходящейся к жесли последовательность
называется равномерно сходящейся к жесли последовательность  частичных сумм, определяемых
частичных сумм, определяемых

равномерно сходится к ж.
Существует аналог теста сравнения для бесконечного ряда функций, называемый М-тест Вейерштрасса.
Критерий сходимости Коши
В Критерий сходимости Коши заявляет, что серия

сходится если и только если последовательность частичные суммы это Последовательность КошиЭто означает, что для каждого  есть положительное целое число
есть положительное целое число  такой, что для всех
такой, что для всех  у нас есть
у нас есть

что эквивалентно

Смотрите также
внешняя ссылка


































![r = limsup _ {n rightarrow infty} { sqrt [{n}] {| a_ {n} |}},](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd5eebb0f17b1155c0bea36edfdd50d6b9aa0f01)





















