WikiDer > Основное дерево
В Информатика, а радиксное дерево (также радикс-три или же компактное префиксное дерево) это структура данных который представляет собой оптимизированный по пространству три (префиксное дерево), в котором каждый узел, являющийся единственным потомком, объединяется со своим родителем. В результате количество дочерних элементов каждого внутреннего узла не превышает основание р коренного дерева, где р положительное целое число и степень Икс из 2, имея Икс ≥ 1. В отличие от обычных деревьев, ребра можно помечать как последовательностями элементов, так и отдельными элементами. Это делает дерево системы счисления более эффективным для небольших наборов (особенно, если строки длинные) и для наборов строк, которые имеют общие длинные префиксы.
В отличие от обычных деревьев (где сравниваются целые ключи в массовом порядке от их начала до точки неравенства), ключ в каждом узле сравнивается по частям битов по частям, где количество битов в этом фрагменте в этом узле является основанием р корня три. Когда р равно 2, основание системы счисления является двоичным (т. е. сравнивает 1-битную часть ключа этого узла), что минимизирует разреженность за счет максимизации глубины дерева, то есть максимизирует до объединения нерасходящихся битовых строк в ключе. Когда р представляет собой целую степень двойки, имеющую р ≥ 4, то основание системы счисления является р-ary trie, который уменьшает глубину корневого дерева за счет потенциальной разреженности.
В качестве оптимизации краевые метки могут быть сохранены с постоянным размером, используя два указателя на строку (для первого и последнего элементов).[1]
Обратите внимание, что хотя примеры в этой статье показывают строки как последовательности символов, тип строковых элементов можно выбрать произвольно; например, как бит или байт строкового представления при использовании многобайтовый символ кодировки или Unicode.
Приложения
Радикс-деревья полезны для построения ассоциативные массивы с ключами, которые могут быть выражены как строки. Они находят особое применение в области IP маршрутизация,[2][3][4] где способность содержать большие диапазоны значений за некоторыми исключениями особенно подходит для иерархической организации IP-адреса.[5] Они также используются для инвертированные индексы текстовых документов в поиск информации.
Операции
Радикс-деревья поддерживают операции вставки, удаления и поиска. Вставка добавляет новую строку в дерево, пытаясь минимизировать объем хранимых данных. Удаление удаляет строку из дерева. Операции поиска включают (но не обязательно ограничиваются) точный поиск, поиск предшественника, поиск преемника и поиск всех строк с префиксом. Все эти операции за O (k) где k - максимальная длина всех строк в наборе, где длина измеряется количеством битов, равным основанию системы счисления системы счисления.
Искать
Операция поиска определяет, существует ли строка в дереве. Большинство операций каким-либо образом изменяют этот подход для решения своих конкретных задач. Например, может иметь значение узел, на котором заканчивается строка. Эта операция аналогична попыткам, за исключением того, что некоторые ребра потребляют несколько элементов.
Следующий псевдокод предполагает, что эти классы существуют.
Край
- Узел targetNode
- нить метка
Узел
- Массив ребер края
- функция isLeaf ()
функция искать(нить Икс){ // Начинаем с корня без найденных элементов Узел traverseNode: = корень; int elementsFound: = 0; // Двигаться до тех пор, пока не будет найден лист, или пока не удастся продолжить пока (traverseNode! = ноль &&! traverseNode.isLeaf () && elementsFound // Получение следующего края для исследования на основе элементов, еще не найденных в x Край nextEdge: = Выбрать край из traverseNode.edges куда край. ярлык является префиксом x.suffix (elementsFound) // x.suffix (elementsFound) возвращает последние (x.length - elementsFound) элементы x // Было найдено ребро? если (nextEdge! = ноль) { // Устанавливаем следующий узел для исследования traverseNode: = nextEdge.targetNode; // Приращение найденных элементов на основе метки, хранящейся на краю elementsFound + = nextEdge.label.length; } еще { // Завершаем цикл traverseNode: = ноль; } } // Соответствие найдено, если мы достигли конечного узла и израсходовали ровно x.length элементов возвращаться (traverseNode! = ноль && traverseNode.isLeaf () && elementsFound == x.length);} Вставка
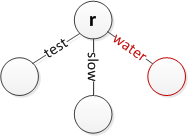
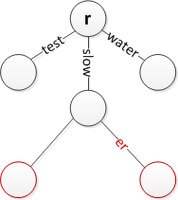
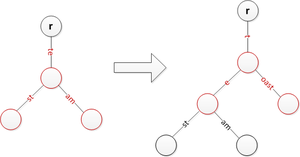
Чтобы вставить строку, мы ищем в дереве, пока не сможем продвинуться дальше. На этом этапе мы либо добавляем новое исходящее ребро, помеченное всеми оставшимися элементами во входной строке, либо, если уже есть исходящее ребро, разделяющее префикс с оставшейся входной строкой, мы разбиваем его на два ребра (первое помечено общим префикс) и продолжайте. Этот шаг разделения гарантирует, что ни один узел не имеет больше дочерних элементов, чем возможных строковых элементов.
Ниже показано несколько случаев вставки, но их может быть и больше. Обратите внимание, что r просто представляет корень. Предполагается, что ребра могут быть помечены пустыми строками для завершения строк там, где это необходимо, и что корень не имеет входящего ребра. (Описанный выше алгоритм поиска не будет работать при использовании ребер пустой строки.)
Удаление
Чтобы удалить строку x из дерева, мы сначала находим лист, представляющий x. Затем, предполагая, что x существует, мы удаляем соответствующий листовой узел. Если родительский элемент нашего листового узла имеет только один другой дочерний элемент, то входящая метка этого дочернего элемента добавляется к входящей метке родительского узла, а дочерний элемент удаляется.
Дополнительные операции
- Найти все строки с общим префиксом: возвращает массив строк, начинающихся с одного префикса.
- Найти предшественника: находит самую большую строку меньше заданной в лексикографическом порядке.
- Найти преемника: находит наименьшую строку больше заданной в лексикографическом порядке.
История
Дональд Р. Моррисон первым описал, что Дональд Кнут, страницы 498-500 в томе III Искусство программирования, называет «деревьями Патрисии» в 1968 году.[6] Гернот Гвехенбергер независимо изобрел и описал структуру данных примерно в то же время.[7] Деревья PATRICIA - это деревья с основанием системы счисления с основанием, равным 2, что означает, что каждый бит ключа сравнивается индивидуально, и каждый узел является двусторонней ветвью (то есть левой и правой).
Сравнение с другими структурами данных
(В следующих сравнениях предполагается, что ключи имеют длину k и структура данных содержит п члены.)
В отличие от сбалансированные деревья, основание системы счисления разрешает поиск, вставку и удаление в O (k) времени, а не O (журнал п). Это не кажется преимуществом, поскольку обычно k ≥ журнал п, но в сбалансированном дереве каждое сравнение представляет собой сравнение строк, требующее O (k) время наихудшего случая, многие из которых на практике медленны из-за длинных общих префиксов (в случае, когда сравнения начинаются с начала строки). В общем, все сравнения требуют постоянного времени, но для этого требуется м сравнения, чтобы найти строку длины м. Radix-деревья могут выполнять эти операции с меньшим количеством сравнений и требовать гораздо меньше узлов.
Однако у корневых деревьев также есть недостатки: поскольку они могут применяться только к строкам элементов или элементам с эффективно обратимым отображением на строки, им не хватает всей универсальности сбалансированных деревьев поиска, которые применяются к любому типу данных с общий заказ. Обратимое отображение на строки можно использовать для создания необходимого полного упорядочения для сбалансированных деревьев поиска, но не наоборот. Это также может быть проблематичным, если тип данных только обеспечивает операция сравнения, но не (де)сериализация операция.
Хеш-таблицы обычно говорят, что ожидаемое время вставки и удаления составляет O (1), но это верно только при рассмотрении вычисления хэша ключа как операции с постоянным временем. При учете хеширования ключа хеш-таблицы ожидали O (k) время вставки и удаления, но в худшем случае может занять больше времени в зависимости от того, как обрабатываются конфликты. Деревья счисления имеют наихудший случай O (k) вставка и удаление. Операции преемника / предшественника основанных на системе счисления деревьев также не реализуются хэш-таблицами.
Варианты
Обычное расширение оснований системы счисления использует два цвета узлов: «черный» и «белый». Чтобы проверить, сохранена ли данная строка в дереве, поиск начинается сверху и следует по краям входной строки до тех пор, пока дальнейший прогресс не будет невозможен. Если строка поиска используется и последний узел является черным узлом, поиск не удался; если он белый, поиск успешен. Это позволяет нам добавлять к дереву большой диапазон строк с общим префиксом, используя белые узлы, а затем удалять небольшой набор «исключений» экономным способом, используя вставка их используют черные узлы.
В HAT-trie - это структура данных с учетом кеширования, основанная на деревьях счисления, которая предлагает эффективное хранение и поиск строк, а также упорядоченные итерации. Производительность, как по времени, так и по пространству, сопоставима с потреблением кеш-памяти. хеш-таблица.[8][9] См. Примечания по реализации HAT trie на [1]
А ПАТРИЦИЯ trie - это особый вариант дерева с основанием 2 (двоичного), в котором вместо того, чтобы явно хранить каждый бит каждого ключа, узлы сохраняют только позицию первого бита, который различает два поддерева. Во время обхода алгоритм проверяет индексированный бит ключа поиска и выбирает левое или правое поддерево по мере необходимости. Известные особенности дерева PATRICIA включают в себя то, что для каждого сохраненного уникального ключа требуется только один узел, что делает PATRICIA намного более компактным, чем стандартное двоичное дерево. Кроме того, поскольку фактические ключи больше не хранятся явным образом, необходимо выполнить одно полное сравнение ключей для индексированной записи, чтобы подтвердить совпадение. В этом отношении PATRICIA имеет определенное сходство с индексированием с использованием хеш-таблицы. [10].
В адаптивное основание системы счисления представляет собой вариант дерева счисления, который объединяет адаптивные размеры узлов в дерево счисления. Одним из основных недостатков обычных оснований системы счисления является использование пространства, поскольку он использует постоянный размер узла на каждом уровне. Основное различие между основанием системы счисления и адаптивным деревом системы счисления состоит в том, что размер каждого узла зависит от количества дочерних элементов, которое увеличивается при добавлении новых записей. Следовательно, адаптивное основание системы счисления позволяет лучше использовать пространство без снижения его скорости.[11][12][13]
Распространенной практикой является смягчение критериев, запрещающих родителям только с одним дочерним элементом в ситуациях, когда родитель представляет действительный ключ в наборе данных. Этот вариант основополагающего дерева обеспечивает более высокую эффективность использования пространства, чем тот, который допускает только внутренние узлы с как минимум двумя дочерними элементами.[14]
Смотрите также
- Префиксное дерево (также известный как Trie)
- Детерминированный ациклический конечный автомат (DAFSA)
- Тернарный поиск пытается
- Хэш-три
- Детерминированные конечные автоматы
- Джуди Массив
- Алгоритм поиска
- Расширяемое хеширование
- Отображенное дерево хеш-массива
- Префиксное хеш-дерево
- Burstsort
- Алгоритм Лулео
- Кодирование Хаффмана
Рекомендации
- ^ Морен, Патрик. «Структуры данных для строк» (PDF). Получено 15 апреля 2012.
- ^ "rtfree (9)". www.freebsd.org. Получено 2016-10-23.
- ^ Регенты Калифорнийского университета (1993). "/sys/net/radix.c". Перекрестная ссылка BSD. NetBSD. Получено 2019-07-25.
Подпрограммы для построения и обслуживания оснований системы счисления для поиска маршрутизации.
- ^ "Бесконтактные, атомарные и общие деревья Radix / Patricia". NetBSD. 2011.
- ^ Книжник, Константин. «Патриция пытается: лучший индекс для префиксного поиска», Журнал доктора Добба, Июнь 2008 г.
- ^ Моррисон, Дональд Р. PATRICIA - Практический алгоритм получения информации, закодированной в буквенно-цифровом формате
- ^ Г. Гвехенбергер, Anwendung einer binären Verweiskettenmethode beim Aufbau von Listen. Elektronische Rechenanlagen 10 (1968), стр. 223–226.
- ^ Аскитис, Николай; Синха, Ранджан (2007). HAT-trie: структура данных для строк на основе Trie с учетом кеширования. Труды 30-й Австралазийской конференции по информатике. 62. С. 97–105. ISBN 1-920682-43-0.
- ^ Аскитис, Николай; Синха, Ранджан (октябрь 2010 г.). «Проектирование масштабируемых, эффективных кеш-памяти и попыток для строк». Журнал VLDB. 19 (5): 633–660. Дои:10.1007 / s00778-010-0183-9.
- ^ Моррисон, Дональд Р. Практический алгоритм получения информации, закодированной в буквенно-цифровом формате
- ^ Кемпер, Альфонс; Эйклер, Андре (2013). Datenbanksysteme, Eine Einführung. 9. С. 604–605. ISBN 978-3-486-72139-3.
- ^ "armon / libart: Адаптивные корневые деревья, реализованные на C". GitHub. Получено 17 сентября 2014.
- ^ http://www-db.in.tum.de/~leis/papers/ART.pdf
- ^ Может ли узел Radix-дерева, представляющий действительный ключ, иметь одного ребенка?
внешняя ссылка
| Викискладе есть медиафайлы по теме Основное дерево. |
- Исследования и справочные материалы по алгоритмам и структурам данных: PATRICIAЛлойд Эллисон, Университет Монаша
- Патрисия Три, Словарь алгоритмов и структур данных NIST
- Критические деревья, к Дэниел Дж. Бернштейн
- Radix Tree API в ядре Linux, Джонатан Корбет
- Карт (основополагающее дерево изменения ключа), автор Пол Жарк
- Адаптивное радикальное дерево: индексирование ARTful для баз данных в основной памятиВиктор Лейс, Альфонс Кемпер, Томас Нойман, Технический университет Мюнхена
Реализации
- Реализация FreeBSD, используется для пейджинга, пересылки и прочего.
- Реализация ядра Linux, используется, среди прочего, для кеширования страниц.
- Стандартная библиотека GNU C ++ имеет trie-реализацию
- Реализация параллельного Radix Tree в Java, автор: Найл Галлахер
- C # реализация Radix Tree
- Библиотека шаблонов практических алгоритмов, библиотека C ++ на PATRICIA пытается (VC ++> = 2003, GCC G ++ 3.x), Роман С. Клюйков
- Патрисия Трие реализация класса шаблона C ++, Раду Грюян
- Реализация стандартной библиотеки Haskell "на основе деревьев патриции с прямым порядком байтов". Доступен для просмотра в Интернете исходный код.
- Реализация Патрисии Три на Java, Роджер Капси и Сэм Берлин
- Критические деревья разветвлен из кода C Дэниэлом Дж. Бернштейном
- Реализация Patricia Trie на C, в libcprops
- Patricia Trees: эффективные множества и отображения целых чисел в OCaml, Жан-Кристоф Филлиатр
- Реализация Radix DB (Patricia trie) на C, Г. Б. Версиани
- Libart - Адаптивные коренные деревья, реализованные на C, Армон Дадгар с другими участниками (открытый исходный код, лицензия BSD с тремя пунктами)
- Реализация в NIM дерева критических битов