WikiDer > Дерево слияния

Fusion tree

В Информатика, а дерево слияния это тип древовидная структура данных который реализует ассоциативный массив на ш-битовые целые числа. При работе с коллекцией п пары "ключ-значение", оно использует О(п) пространство и выполняет поиск в О(бревнош п) время, которое асимптотически быстрее, чем традиционный самобалансирующееся двоичное дерево поиска, а также лучше, чем дерево ван Эмде Боас для больших значенийш. Эта скорость достигается за счет использования определенных операций с постоянным временем, которые могут выполняться на машинное слово. Деревья фьюжн были изобретены в 1990 году Майкл Фредман и Дэн Уиллард.[1]

Со времени выхода оригинальной статьи Фредмана и Уилларда 1990 года было сделано несколько успехов. В 1999 году[2] было показано, как реализовать деревья слияния в рамках модели вычислений, в которой все базовые операции алгоритма принадлежат AC0, модель сложность схемы который разрешает сложение и побитовые логические операции, но запрещает операции умножения, используемые в исходном алгоритме слияния. Динамическая версия деревьев слияния с использованием хеш-таблицы был предложен в 1996 г.[3] что соответствовало исходной структуре О(бревнош п) время выполнения в ожидании. Другая динамическая версия с использованием экспоненциальное дерево был предложен в 2007 г.[4] что дает время выполнения в худшем случае О(бревнош п + журнал журнал п) за операцию. Остается открытым, могут ли деревья динамического слияния достичь О(бревнош п) за операцию с большой вероятностью.

Как это устроено

Дерево слияния - это, по сути, B-дерево с фактором ветвления ш1/5 (возможен также любой малый показатель степени), что дает ему высоту О(бревнош п). Чтобы достичь желаемого времени выполнения обновлений и запросов, дерево слияния должно иметь возможность искать узел, содержащий до ш1/5 ключи в постоянное время. Это делается путем сжатия («зарисовки») ключей так, чтобы все они могли уместиться в одно машинное слово, что, в свою очередь, позволяет проводить сравнения параллельно.

Эскиз

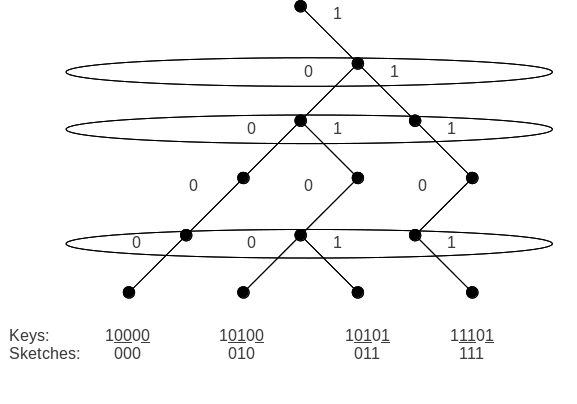
Эскиз - это метод, с помощью которого каждый ш-битовый ключ на узле, содержащем k ключи сжаты только в k − 1 биты. Каждый ключ Икс можно рассматривать как путь в полном двоичном дереве высоты ш начиная с корня и заканчивая листом, соответствующим Икс. Чтобы различить два пути, достаточно посмотреть на их точку ветвления (первый бит, в котором два ключа различаются). Все k пути вместе имеют k − 1 точки ветвления, поэтому не более k − 1 биты необходимы, чтобы различать любые два из k ключи.

Визуализация функции эскиза.

Важным свойством функции эскиза является то, что она сохраняет порядок клавиш. Это, эскиз (Икс) <эскиз (у) для любых двух ключей Икс < у.

Аппроксимация эскиза

Если расположение битов эскиза б1 < б2 < ··· < бр, затем эскиз ключа Иксш-1···Икс1Икс0 это р-битовое целое число .

С помощью только стандартных операций со словами, таких как Язык программирования C, трудно напрямую вычислить эскиз ключа за постоянное время. Вместо этого биты эскиза могут быть упакованы в диапазоне размеров не более р4, с помощью побитовое И и умножение. Побитовая операция И служит для очистки ключа от всех битов, не относящихся к скетчу, в то время как умножение сдвигает биты скетча в небольшой диапазон. Как и в «идеальном» эскизе, в приблизительном эскизе сохраняется порядок клавиш.

Для определения правильной константы умножения требуется некоторая предварительная обработка. Каждый эскиз на месте бя будет перенесено на бя + мя умножением на м = 2мя. Чтобы приблизительный эскиз работал, должны выполняться следующие три свойства:

  1. бя + мj различны для всех пар (я, j). Это гарантирует, что биты эскиза не будут повреждены умножением.
  2. бя + мя является строго возрастающей функцией я. То есть порядок битов эскиза сохраняется.
  3. (бр + мр) - (б1 + м1) ≤ р4. То есть биты эскиза упакованы в диапазоне размеров не более р4.

Индуктивный аргумент показывает, как мя могут быть построены. Позволять м1 = ш − б1. Предположим, что 1 < т ≤ р и это м1, м2... мт-1 уже выбраны. Затем выберите наименьшее целое число мт такая, что выполняются оба свойства (1) и (2). Свойство (1) требует, чтобы мт ≠ бя − бj + мл для всех 1 ≤ я, j ≤ р и 1 ≤ л ≤ т-1. Таким образом, меньше чем tr2 ≤ р3 ценности, которые мт следует избегать. С мт выбирается минимальным, (бт + мт) ≤ (бт-1 + мт-1) + р3. Отсюда следует свойство (3).

Таким образом, приблизительный эскиз рассчитывается следующим образом:

  1. Замаскируйте все, кроме фрагментов эскиза, с помощью побитового AND.
  2. Умножьте ключ на заданную константу м. На самом деле для этой операции требуются два машинных слова, но все же это можно сделать за постоянное время.
  3. Замаскируйте все, кроме смещенных фрагментов эскиза. Теперь они содержатся в непрерывном блоке не более р4 < ш4/5 биты.

Параллельное сравнение

Цель сжатия, достигаемого с помощью эскиза, - позволить хранить все ключи в одном ш-битное слово. Пусть эскиз узла узла быть битовой строкой

1эскиз(Икс1)1эскиз(Икс2)...1эскиз(Иксk)

Можно предположить, что функция скетча использует ровно б ≤ р4 биты. Тогда каждый блок использует 1 + б ≤ ш4/5 биты, и поскольку k ≤ ш1/5, общее количество бит в эскизе узла не превышает ш.

Небольшие обозначения в сторону: для битовой строки s и неотрицательное целое число м, позволять sм обозначают конкатенацию s себе м раз. Если т также битовая строка ул обозначает конкатенацию т к s.

Скетч узла позволяет искать ключи для любых б-битовое целое число у. Позволять z = (0у)k, который можно вычислить за постоянное время (умножить у на константу (0б1)k). Обратите внимание, что 1эскиз(Икся) - 0у всегда положительно, но сохраняет свою ведущую единицу тогда и только тогда, когда эскиз(Икся) ≥ у. Таким образом, мы можем вычислить наименьший индекс я такой, что эскиз(Икся) ≥ у следующим образом:

  1. Вычесть z из эскиза узла.
  2. Возьмите побитовое И разности и константы (10б)k. Это очищает все, кроме ведущего бита каждого блока.
  3. Найти старший бит результата.
  4. Вычислить я, используя тот факт, что ведущий бит я-й блок имеет индекс я(б+1).

Рисование

По произвольному запросу q, параллельное сравнение вычисляет индекс я такой, что

эскиз(Икся-1) ≤ эскиз(q) ≤ эскиз(Икся)

К сожалению, функция эскиза, как правило, не сохраняет порядок вне набора клавиш, поэтому это не обязательно так, что Икся-1 ≤ q ≤ Икся. Верно то, что среди всех ключей либо Икся-1 или Икся имеет самый длинный общий префикс с q. Это потому, что любой ключ у с более длинным общим префиксом с q также будет иметь больше скетчей, общих с q, и поэтому эскиз(у) будет ближе к эскиз(q) чем любой эскиз(Иксj).

Самый длинный общий префикс между двумя ш-битовые целые числа а и б можно вычислить за постоянное время, найдя самый старший бит побитовое XOR между а и б. Затем это можно использовать, чтобы замаскировать все, кроме самого длинного общего префикса.

Обратите внимание, что п точно определяет, где q ответвляется от набора ключей. Если следующий бит q равно 0, то наследник q содержится в п1 поддерево, и если следующий бит q равно 1, то предшественник q содержится в п0 поддерево. Это предполагает следующий алгоритм:

  1. Используйте параллельное сравнение, чтобы найти индекс я такой, что эскиз(Икся-1) ≤ эскиз(q) ≤ эскиз(Икся).
  2. Вычислить самый длинный общий префикс п из q и либо Икся-1 или Икся (принимая более длительный из двух).
  3. Позволять л-1 - длина самого длинного общего префикса п.
    1. Если л-й бит q равно 0, пусть е = п10ш-л. Используйте параллельное сравнение для поиска преемника эскиз(е). Это фактический предшественник q.
    2. Если л-й бит q равно 1, пусть е = п01ш-л. Используйте параллельное сравнение для поиска предшественника эскиз(е). Это фактический преемник q.
  4. Когда-то либо предшественник, либо преемник q найдено точное положение q среди набора ключей определяется.

Фьюжн хеширование

Применение деревьев слияния для хеш-таблицы был дан Уиллардом, который описывает структуру данных для хеширования, в которой хеш-таблица внешнего уровня с хеш-цепочкой объединена с деревом слияния, представляющим каждую хеш-цепочку. В хеш-цепочке в хеш-таблице с постоянным коэффициентом загрузки среднее размер цепочки постоянен, но при этом с большой вероятностью все цепочки имеют размер О(бревно п / журнал журнал п), где п - количество хешированных элементов. Этот размер цепочки достаточно мал, чтобы дерево слияния могло обрабатывать поиск и обновления в нем за постоянное время для каждой операции. Следовательно, время для всех операций в структуре данных с большой вероятностью постоянно. Точнее, с этой структурой данных для каждого обратногоквазиполином вероятность п(п) = exp ((журнал п)О(1)), есть постоянная C такая, что вероятность того, что существует операция, превышающая время C самое большее п(п).[5]

Рекомендации

  1. ^ Фредман, М.Л.; Уиллард, Д. Э. (1990), "Взрыв через теоретический информационный барьер с помощью FUSION TREES", Материалы двадцать второго ежегодного ACM Симпозиум по теории вычислений (STOC '90), Нью-Йорк, Нью-Йорк, США: ACM, стр. 1–7, Дои:10.1145/100216.100217, ISBN 0-89791-361-2.
  2. ^ Андерссон, Арне; Милтерсен, Питер Бро; Торуп, Миккель (1999), «Деревья слияния могут быть реализованы с AC0 только инструкции ", Теоретическая информатика, 215 (1–2): 337–344, Дои:10.1016 / S0304-3975 (98) 00172-8, Г-Н 1678804.
  3. ^ Раман, Раджив (1996), "Приоритетные очереди: маленькие, монотонные и трансдихотомические", Четвертый ежегодный европейский симпозиум по алгоритмам (ESA '96), Барселона, Испания, 25–27 сентября 1996 г., Конспект лекций по информатике, 1136, Берлин: Springer-Verlag, стр. 121–137, Дои:10.1007/3-540-61680-2_51, Г-Н 1469229.
  4. ^ Андерссон, Арне; Торуп, Миккель (2007), «Динамические упорядоченные множества с экспоненциальными деревьями поиска», Журнал ACM, 54 (3): A13, arXiv:cs / 0210006, Дои:10.1145/1236457.1236460, Г-Н 2314255.
  5. ^ Уиллард, Дэн Э. (2000), «Исследование вычислительной геометрии, деревьев Ван Эмде Боаса и хеширования с точки зрения дерева слияния», SIAM Журнал по вычислениям, 29 (3): 1030–1049, Дои:10.1137 / S0097539797322425, Г-Н 1740562.

внешняя ссылка