WikiDer > Дерево интервалов

В Информатика, дерево интервалов это древовидная структура данных держать интервалы. В частности, он позволяет эффективно находить все интервалы, которые перекрываются с любым заданным интервалом или точкой. Это часто^{[нужна цитата]} используется для оконных запросов, например, чтобы найти все дороги на компьютерной карте внутри прямоугольного окна просмотра или найти все видимые элементы внутри трехмерной сцены. Похожая структура данных - это дерево сегментов.

Тривиальное решение - посетить каждый интервал и проверить, пересекает ли он заданную точку или интервал, что требует ${ Displaystyle О (п)}$ время, где ${ displaystyle n}$ - количество интервалов в коллекции. Поскольку запрос может возвращать все интервалы, например, если запрос представляет собой большой интервал, пересекающий все интервалы в коллекции, это асимптотически оптимальный; однако мы можем добиться большего, если рассмотрим алгоритмы, чувствительные к выходу, где время выполнения выражается через ${ displaystyle m}$, количество интервалов, созданных запросом. Деревья интервалов имеют время запроса ${ Displaystyle О ( журнал п + м)}$ и начальное время создания ${ Displaystyle О (п журнал п)}$, ограничивая потребление памяти до ${ Displaystyle О (п)}$. После создания деревья интервалов могут быть динамическими, что позволяет эффективно вставлять и удалять интервалы в ${ Displaystyle О ( журнал п)}$ время. Если конечные точки интервалов находятся в небольшом целочисленном диапазоне (например, В диапазоне ${ Displaystyle [1, ldots, О (п)]}$), существуют более быстрые и фактически оптимальные структуры данных^[1][2] со временем предварительной обработки ${ Displaystyle О (п)}$ и время запроса ${ Displaystyle О (1 + м)}$ для отчетности ${ displaystyle m}$ интервалы, содержащие данную точку запроса (см.^[1] для очень простого).

Наивный подход

В простом случае интервалы не перекрываются и их можно вставить в простой двоичное дерево поиска и запрошено в ${ Displaystyle О ( журнал п)}$ время. Однако с произвольно перекрывающимися интервалами невозможно сравнить два интервала для вставки в дерево, поскольку порядок сортировки по начальным или конечным точкам может быть различным. Наивный подход может заключаться в построении двух параллельных деревьев, одно из которых упорядочено по начальной точке, а второе - по конечной точке каждого интервала. Это позволяет отбрасывать половину каждого дерева в ${ Displaystyle О ( журнал п)}$ время, но результаты должны быть объединены, что требует ${ Displaystyle О (п)}$ время. Это дает нам вопросы в ${ Displaystyle О (п + журнал п) = О (п)}$, что не лучше брутфорса.

Деревья интервалов решают эту проблему. В этой статье описаны два альтернативных варианта построения интервального дерева, получившего название центрированное дерево интервалов и дополненное дерево.

Центрированное дерево интервалов

Запросы требуют ${ Displaystyle О ( журнал п + м)}$ время, с ${ displaystyle n}$ общее количество интервалов и ${ displaystyle m}$ количество полученных результатов. Строительство требует ${ Displaystyle О (п журнал п)}$ время и хранение требует ${ Displaystyle О (п)}$ Космос.

Строительство

Учитывая набор ${ displaystyle n}$ интервалы на числовой прямой, мы хотим построить структуру данных, чтобы мы могли эффективно извлекать все интервалы, перекрывающие другой интервал или точку.

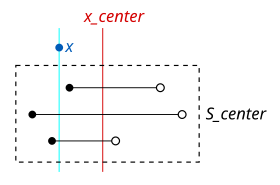
Мы начинаем с того, что берем весь диапазон всех интервалов и делим его пополам на ${ displaystyle x _ { textrm {center}}}$ (на практике, ${ displaystyle x _ { textrm {center}}}$ следует собирать, чтобы дерево оставалось относительно сбалансированным). Это дает три набора интервалов, которые полностью слева от ${ displaystyle x _ { textrm {center}}}$ который мы назовем ${ displaystyle S _ { textrm {left}}}$, полностью справа от ${ displaystyle x _ { textrm {center}}}$ который мы назовем ${ displaystyle S _ { textrm {right}}}$, и перекрывающиеся ${ displaystyle x _ { textrm {center}}}$ который мы назовем ${ displaystyle S _ { textrm {center}}}$.

Интервалы в ${ displaystyle S _ { textrm {left}}}$ и ${ displaystyle S _ { textrm {right}}}$ рекурсивно делятся таким же образом, пока не кончатся интервалы.

Интервалы в ${ displaystyle S _ { textrm {center}}}$ которые перекрывают центральную точку, хранятся в отдельной структуре данных, связанной с узлом в дереве интервалов. Эта структура данных состоит из двух списков, один из которых содержит все интервалы, отсортированные по их начальным точкам, а другой - все интервалы, отсортированные по их конечным точкам.

В результате двоичное дерево с каждым узлом, хранящим:

• Центральная точка
• Указатель на другой узел, содержащий все интервалы полностью слева от центральной точки
• Указатель на другой узел, содержащий все интервалы полностью справа от центральной точки
• Все интервалы, перекрывающие центральную точку, отсортированы по их начальной точке
• Все интервалы, перекрывающие центральную точку, отсортированы по конечной точке

Пересекающиеся

Учитывая структуру данных, построенную выше, мы получаем запросы, состоящие из диапазонов или точек, и возвращаем все диапазоны в исходном наборе, перекрывающие этот ввод.

С точкой

Задача - найти в дереве все интервалы, которые перекрывают заданную точку. ${ displaystyle x}$. Обход дерева выполняется с помощью аналогичного рекурсивного алгоритма, который использовался бы для обхода традиционного двоичного дерева, но с дополнительной логикой для поддержки поиска интервалов, перекрывающих «центральную» точку в каждом узле.

Для каждого узла дерева ${ displaystyle x}$ сравнивается с ${ displaystyle x _ { textrm {center}}}$, средняя точка, используемая при построении узла выше. Если ${ displaystyle x}$ меньше чем ${ displaystyle x _ { textrm {center}}}$, крайний левый набор интервалов, ${ displaystyle S _ { textrm {left}}}$, Считается. Если ${ displaystyle x}$ больше, чем ${ displaystyle x _ { textrm {center}}}$, крайний правый набор интервалов, ${ displaystyle S _ { textrm {right}}}$, Считается.

Все интервалы в ${ displaystyle S _ { textrm {center}}}$ что начинается раньше ${ displaystyle x}$ должен перекрываться ${ displaystyle x}$ если ${ displaystyle x}$ меньше чем ${ displaystyle x _ { textrm {center}}}$.
Точно так же тот же метод применяется при проверке заданного интервала. Если данный интервал заканчивается на у и у меньше чем ${ displaystyle x _ { textrm {center}}}$, все интервалы в ${ displaystyle S _ { textrm {center}}}$ что начинается раньше у также должен перекрывать заданный интервал.

Поскольку каждый узел обрабатывается при прохождении дерева от корня до листа, диапазоны в его ${ displaystyle S _ { textrm {center}}}$ обрабатываются. Если ${ displaystyle x}$ меньше чем ${ displaystyle x _ { textrm {center}}}$, мы знаем, что все интервалы в ${ displaystyle S _ { textrm {center}}}$ конец после ${ displaystyle x}$, иначе они не могли перекрываться ${ displaystyle x}$. Следовательно, нам нужно только найти эти интервалы в ${ displaystyle S _ { textrm {center}}}$ что начинается раньше ${ displaystyle x}$. Мы можем ознакомиться со списками ${ displaystyle S _ { textrm {center}}}$ которые уже построены. Поскольку в этом сценарии нас интересуют только начала интервала, мы можем просмотреть список, отсортированный по началу. Предположим, мы находим ближайшее число не больше, чем ${ displaystyle x}$ в этом списке. Все диапазоны от начала списка до найденной точки перекрываются ${ displaystyle x}$ потому что они начинаются раньше ${ displaystyle x}$ и закончить после ${ displaystyle x}$ (как мы знаем, потому что они перекрываются ${ displaystyle x _ { textrm {center}}}$ что больше чем ${ displaystyle x}$). Таким образом, мы можем просто начать перечисление интервалов в списке, пока значение начальной точки не превысит ${ displaystyle x}$.

Аналогично, если ${ displaystyle x}$ больше, чем ${ displaystyle x _ { textrm {center}}}$, мы знаем, что все интервалы в ${ displaystyle S _ { textrm {center}}}$ должен начаться раньше ${ displaystyle x}$, поэтому мы находим те интервалы, которые заканчиваются после ${ displaystyle x}$ используя список, отсортированный по окончанию интервалов.

Если ${ displaystyle x}$ точно соответствует ${ displaystyle x _ { textrm {center}}}$, все интервалы в ${ displaystyle S _ { textrm {center}}}$ могут быть добавлены к результатам без дальнейшей обработки, а обход дерева может быть остановлен.

С интервалом

За интервал результата ${ displaystyle r}$ чтобы пересечь наш интервал запроса ${ displaystyle q}$ должно выполняться одно из следующих условий:

• начальная и / или конечная точка ${ displaystyle r}$ в ${ displaystyle q}$; или же
• ${ displaystyle r}$ полностью закрывает ${ displaystyle q}$.

Эта статья может быть сбивает с толку или неясно читателям. Пожалуйста, помоги нам прояснить статью. Возможно обсуждение этого вопроса на страница обсуждения. (Февраль 2020 г.) (Узнайте, как и когда удалить этот шаблон сообщения)

Сначала мы находим все интервалы с начальной и / или конечной точками внутри ${ displaystyle q}$ с помощью отдельно построенного дерева. В одномерном случае мы можем использовать дерево поиска, содержащее все начальные и конечные точки в наборе интервалов, каждая из которых имеет указатель на соответствующий интервал. Бинарный поиск в ${ Displaystyle О ( журнал п)}$ время для начала и конца ${ displaystyle q}$ показывает минимальные и максимальные точки для рассмотрения. Каждая точка в этом диапазоне ссылается на интервал, который перекрывает ${ displaystyle q}$ и добавляется в список результатов. Следует проявлять осторожность, чтобы избежать дублирования, поскольку интервал может начинаться и заканчиваться в пределах ${ displaystyle q}$. Это можно сделать с помощью двоичного флага на каждом интервале, чтобы отметить, был ли он добавлен в набор результатов.

Наконец, мы должны найти интервалы, которые заключают ${ displaystyle q}$. Чтобы найти их, мы выбираем любую точку внутри ${ displaystyle q}$ и используйте описанный выше алгоритм, чтобы найти все интервалы, пересекающие эту точку (опять же, стараясь удалить дубликаты).

Высшие измерения

Структуру данных дерева интервалов можно обобщить до более высокого измерения. ${ displaystyle N}$ с одинаковым временем запроса и построения и ${ Displaystyle О (п журнал п)}$ Космос.

Первый дерево диапазона в ${ displaystyle N}$ размеры построены, что позволяет эффективно извлекать все интервалы с начальной и конечной точками внутри области запроса ${ displaystyle R}$. После того, как соответствующие диапазоны найдены, остается только те диапазоны, которые охватывают область в некотором измерении. Чтобы найти эти совпадения, ${ displaystyle N}$ создаются деревья интервалов, и одна ось пересекает ${ displaystyle R}$ запрашивается для каждого. Например, в двух измерениях нижняя часть квадрата ${ displaystyle R}$ (или любая другая горизонтальная линия, пересекающая ${ displaystyle R}$) будет запрашиваться в дереве интервалов, построенном для горизонтальной оси. Аналогично, левая (или любая другая вертикальная линия, пересекающая ${ displaystyle R}$) будет запрашиваться в дереве интервалов, построенном на вертикальной оси.

Каждое дерево интервалов также нуждается в добавлении для более высоких измерений. В каждом узле мы проходим по дереву, ${ displaystyle x}$ сравнивается с ${ displaystyle S _ { textrm {center}}}$ найти совпадения. Вместо двух отсортированных списков точек, которые использовались в одномерном случае, строится дерево диапазонов. Это позволяет эффективно извлекать все точки в ${ displaystyle S _ { textrm {center}}}$ эта область перекрытия ${ displaystyle R}$.

Удаление

Если после удаления интервала из дерева узел, содержащий этот интервал, больше не содержит интервалов, этот узел может быть удален из дерева. Это сложнее, чем обычная операция удаления двоичного дерева.

Интервал может перекрывать центральную точку нескольких узлов в дереве. Поскольку каждый узел хранит интервалы, которые перекрывают его, причем все интервалы полностью находятся слева от его центральной точки в левом поддереве, аналогично для правого поддерева, из этого следует, что каждый интервал хранится в узле, ближайшем к корню из набора узлы, центральная точка которых перекрывается.

Обычные операции удаления в двоичном дереве (для случая, когда удаляемый узел имеет двух дочерних элементов) включают продвижение узла дальше от листа до положения удаляемого узла (обычно крайний левый дочерний элемент правого поддерева или крайний правый дочерний элемент. левого поддерева).

Удаление узла с двумя дочерними элементами из двоичного дерева поиска с помощью упорядоченного предшественника (крайний правый узел в левом поддереве, помеченный 6).

В результате этого продвижения некоторые узлы, которые находились выше продвинутого узла, станут его потомками; необходимо найти в этих узлах интервалы, которые также перекрывают продвинутый узел, и переместить эти интервалы в продвинутый узел. Как следствие, это может привести к появлению новых пустых узлов, которые необходимо удалить, снова следуя тому же алгоритму.

Балансировка

Те же проблемы, которые влияют на удаление, также влияют на операции вращения; вращение должно сохранять неизменным тот факт, что узлы хранятся как можно ближе к корню.

Дополненное дерево

Расширенное дерево с низким значением в качестве ключа и максимальным значением в качестве дополнительной аннотации.

Например, при проверке заданного интервала [40 ,60) перекрывает интервалы в дереве, показанном выше, мы видим, что он не перекрывает интервал [20, 36) в корне, но поскольку низкое значение корня (20) меньше искомого высокого значения (60), мы должны искать правое поддерево. Максимальный максимум левого поддерева, равный 41, превышает искомое меньшее значение (40), поэтому мы также должны искать левое поддерево. Однако оба потомка [3, 41) Максимальные значения узла меньше 40, поэтому поиск левого поддерева на этом заканчивается, и нет необходимости искать их.

Другой способ представления интервалов описан в Cormen et al. (2009 г., Раздел 14.3: Деревья интервалов, стр. 348–354).

И для вставки, и для удаления требуется ${ Displaystyle О ( журнал п)}$ время, с ${ displaystyle n}$ это общее количество интервалов в дереве до операции вставки или удаления.

Расширенное дерево может быть построено из простого упорядоченного дерева, например двоичное дерево поиска или же самобалансирующееся двоичное дерево поиска, упорядоченные по «низким» значениям интервалов. Затем к каждому узлу добавляется дополнительная аннотация, в которой записывается максимальное верхнее значение среди всех интервалов, начиная с этого узла. Поддержание этого атрибута включает обновление всех предков узла снизу вверх при каждом добавлении или удалении узла. Это займет всего O (час) шагов на добавление или удаление узла, где час высота узла, добавляемого или удаляемого в дереве. Если есть вращения деревьев во время вставки и удаления затронутые узлы также могут нуждаться в обновлении.

Теперь известно, что два интервала ${ displaystyle A}$ и ${ displaystyle B}$ перекрываются только тогда, когда оба ${ displaystyle A _ { textrm {low}} leq B _ { textrm {high}}}$ и ${ displaystyle A _ { textrm {high}} geq B _ { textrm {low}}}$. При поиске в деревьях узлов, перекрывающихся с заданным интервалом, вы можете сразу пропустить:

• все узлы справа от узлов, нижнее значение которых превышает конец данного интервала.
• все узлы, которые имеют максимальное максимальное значение ниже начала данного интервала.

Запросы о членстве

Некоторая производительность может быть достигнута, если дерево избегает ненужных обходов. Это может происходить при добавлении уже существующих интервалов или удалении несуществующих интервалов.

Общий порядок интервалов можно определить, упорядочив их сначала по нижним границам, а затем по верхним границам. Затем проверка членства может быть выполнена в ${ Displaystyle О ( журнал п)}$ время, по сравнению с ${ Displaystyle О (к + журнал п)}$ время, необходимое для поиска дубликатов, если ${ displaystyle k}$ интервалы перекрывают интервал, который нужно вставить или удалить. Это решение имеет то преимущество, что не требует дополнительных конструкций. Изменение строго алгоритмическое. Недостатком является то, что запросы о членстве принимают ${ Displaystyle О ( журнал п)}$ время.

Поочередно, из расчета ${ Displaystyle О (п)}$ памяти, запросы членства в ожидаемое постоянное время могут быть реализованы с помощью хэш-таблицы, обновляемой синхронно с деревом интервалов. Это не обязательно может удвоить общую потребность в памяти, если интервалы хранятся по ссылке, а не по значению.

Пример Java: добавление нового интервала в дерево

Ключом каждого узла является сам интервал, поэтому узлы упорядочиваются сначала по низкому значению и, наконец, по высокому значению, а значение каждого узла является конечной точкой интервала:

 общественный пустота Добавить(Интервал я) {     положить(я, я.getEnd()); }

Пример Java: поиск точки или интервала в дереве

Чтобы найти интервал, нужно пройти по дереву, используя ключ (n.getKey ()) и высокое значение (n.getValue ()), чтобы исключить ветки, которые не могут перекрывать запрос. Самый простой случай - это точечный запрос:

 // Ищем все интервалы, содержащие "p", начиная с // узел "n" и добавление подходящих интервалов в список "result" общественный пустота поиск(IntervalNode п, Точка п, Список<Интервал> результат) {     // Не ищите узлы, которые не существуют     если (п == ноль)         возвращаться;     // Если p находится справа от крайней правой точки любого интервала     // в этом узле и во всех дочерних элементах совпадений не будет.     если (п.сравнить с(п.getValue()) > 0)         возвращаться;     // Поиск левых потомков     поиск(п.getLeft(), п, результат);     // Проверяем этот узел     если (п.getKey().содержит(п))         результат.Добавить(п.getKey());     // Если p находится слева от начала этого интервала,     // тогда он не может быть ни в одном дочернем элементе справа.     если (п.сравнить с(п.getKey().начать()) < 0)         возвращаться;     // В противном случае ищем правильных потомков     поиск(п.быть правым(), п, результат); }

куда

а.сравнить с(б) возвращает отрицательное значение, если a

а.сравнить с(б) возвращает ноль, если a = b

а.сравнить с(б) возвращает положительное значение, если a> b

Код для поиска интервала аналогичен, за исключением галочки посередине:

 // Проверяем этот узел если (п.getKey().пересекается с(я))     результат.Добавить (п.getKey());

пересекается с() определяется как:

 общественный логический пересекается с(Интервал Другой) {     возвращаться Начните.сравнить с(Другой.getEnd()) <= 0 &&            конец.сравнить с(Другой.начать()) >= 0; }

Высшие измерения

Расширенные деревья можно расширить до более высоких измерений, циклически перебирая измерения на каждом уровне дерева. Например, для двух измерений нечетные уровни дерева могут содержать диапазоны для Икс-координат, а четные уровни содержат диапазоны для у-координат. Этот подход эффективно преобразует структуру данных из расширенного двоичного дерева в расширенное kd-дерево, что значительно усложняет алгоритмы балансировки вставок и удалений.

Более простое решение - использовать вложенные деревья интервалов. Сначала создайте дерево, используя диапазоны для у-координат. Теперь для каждого узла в дереве добавьте еще одно дерево интервалов на Икс-диапазоны для всех элементов, у-range такой же, как у этого узла у-классифицировать.

Преимущество этого решения заключается в том, что его можно расширить до произвольного количества измерений с использованием той же кодовой базы.

Поначалу дополнительные затраты на вложенные деревья могут показаться непомерно высокими, но обычно это не так. Как и в случае с не вложенным ранее решением, на каждый Икс-координата, давая одинаковое количество узлов для обоих решений. Единственные дополнительные накладные расходы - это вложенные древовидные структуры, по одной на вертикальный интервал. Эта структура обычно незначительного размера, состоящая только из указателя на корневой узел и, возможно, количества узлов и глубины дерева.

Дерево, ориентированное по медиальной плоскости или длине

Эта секция не цитировать любой источники. Пожалуйста помоги улучшить этот раздел к добавление цитат в надежные источники. Материал, не полученный от источника, может быть оспорен и удаленный. (Октябрь 2016) (Узнайте, как и когда удалить этот шаблон сообщения)

Дерево с медиальной ориентацией или длиной похоже на расширенное дерево, но симметрично, с двоичным деревом поиска, упорядоченным по средним точкам интервалов. Максимально ориентированный двоичная куча в каждом узле, отсортированном по длине интервала (или половине длины). Также мы храним минимальное и максимальное возможное значение поддерева в каждом узле (таким образом, симметрия).

Тест на перекрытие

Использование только начального и конечного значений двух интервалов ${ displaystyle left (a_ {i}, b_ {i} right)}$, за ${ Displaystyle я = 0,1}$, тест на перекрытие можно выполнить следующим образом:

${ displaystyle a_ {0}$ и ${ displaystyle a_ {1}> b_ {0}}$

Это можно упростить, используя сумму и разницу:

${ displaystyle s_ {i} = a_ {i} + b_ {i}}$

${ displaystyle d_ {i} = b_ {i} -a_ {i}}$

Это сокращает тест на перекрытие до:

${ displaystyle left | s_ {1} -s_ {0} right |$

Добавление интервала

Добавление новых интервалов в дерево такое же, как для двоичного дерева поиска с использованием среднего значения в качестве ключа. Мы толкаем ${ displaystyle d_ {i}}$ в двоичную кучу, связанную с узлом, и обновить минимальные и максимальные возможные значения, связанные со всеми вышестоящими узлами.

Поиск всех перекрывающихся интервалов

Давайте использовать ${ displaystyle a_ {q}, b_ {q}, m_ {q}, d_ {q}}$ для интервала запроса и ${ displaystyle M_ {n}}$ для ключа узла (по сравнению с ${ displaystyle m_ {i}}$ интервалов)

Начиная с корневого узла, в каждом узле сначала мы проверяем, возможно ли, что наш интервал запроса перекрывается с поддеревом узла, используя минимальные и максимальные значения узла (если это не так, мы не продолжаем для этого узла).

Затем мы вычисляем ${ Displaystyle мин влево {d_ {я} вправо }}$ для интервалов внутри этого узла (не его дочерних), чтобы перекрыть интервал запроса (зная ${ displaystyle m_ {i} = M_ {n}}$):

${ displaystyle min left {d_ {i} right } = left | m_ {q} -M_ {n} right | -d_ {q}}$

и выполнить запрос к его двоичной куче для ${ displaystyle d_ {i}}$больше чем ${ Displaystyle мин влево {d_ {я} вправо }}$

Затем мы проходим через правого и левого потомков узла, делая то же самое.

В худшем случае мы должны сканировать все узлы двоичного дерева поиска, но, поскольку запрос двоичной кучи является оптимальным, это приемлемо (двумерная задача не может быть оптимальной в обоих измерениях)

Ожидается, что этот алгоритм будет быстрее, чем традиционное дерево интервалов (расширенное дерево) для операций поиска. На практике добавление элементов происходит немного медленнее, хотя порядок увеличения такой же.

Рекомендации

• Марк де Берг, Марк ван Кревельд, Марк Овермарс, и Отфрид Шварцкопф. Вычислительная геометрия, Второе исправленное издание. Springer-Verlag 2000. Раздел 10.1: Интервальные деревья, стр. 212–217.
• Кормен, Томас Х.; Лейзерсон, Чарльз Э.; Ривест, Рональд Л.; Штейн, Клиффорд (2009), Введение в алгоритмы (3-е изд.), MIT Press и McGraw-Hill, ISBN 978-0-262-03384-8
• Франко П. Препарата и Майкл Ян Шамос. Вычислительная геометрия: введение. Springer-Verlag, 1985 г.

внешняя ссылка

• CGAL: библиотека алгоритмов вычислительной геометрии на C ++ содержит надежную реализацию Range Trees
• Boost.Icl предлагает C ++ реализации наборов интервалов и карт.
• IntervalTree (Python) - центрированное дерево интервалов с балансировкой AVL, совместимое с тегированными интервалами
• Дерево интервалов (C #) - расширенное дерево интервалов с балансировкой AVL
• Дерево интервалов (Рубин) - центрированное дерево интервалов, неизменяемое, совместимое с помеченными интервалами
• IntervalTree (Java) - расширенное дерево интервалов с балансировкой AVL, поддержкой перекрытия, поиска, интерфейса сбора, интервалов, связанных с идентификатором