WikiDer > Равнодействующая сила

Эта статья нужны дополнительные цитаты для проверка. Пожалуйста помоги улучшить эту статью к добавление цитат в надежные источники. Материал, не полученный от источника, может быть оспорен и удален. Найдите источники: "Равнодействующая сила" – Новости · газеты · книги · ученый · JSTOR (Июнь 2020 г.) (Узнайте, как и когда удалить этот шаблон сообщения)

Графическое представление результирующей силы

В физика и инженерное дело, а Равнодействующая сила единственный сила и связанные крутящий момент получается путем сочетания системы сил и моментов, действующих на жесткое тело. Определяющая черта результирующей силы или результирующей силы-момента заключается в том, что она оказывает такое же влияние на твердое тело, как исходная система сил.^[1] Расчет и визуализация результирующей силы, действующей на тело, выполняется с помощью вычислительного анализа или (в случае достаточно простых систем) диаграмма свободного тела.

Точка приложения результирующей силы определяет связанный с ней крутящий момент. Период, термин Равнодействующая сила следует понимать как относящиеся как к силам, так и к моментам, действующим на твердое тело, поэтому некоторые используют термин результирующая сила-момент.

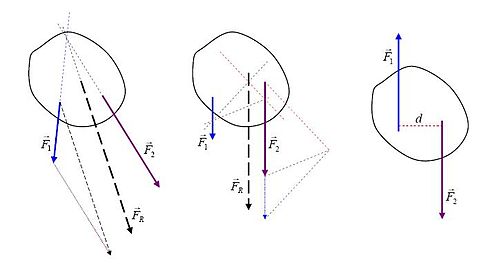
Иллюстрация

Схема иллюстрирует простые графические методы поиска линии приложения равнодействующей силы простых плоских систем.

1. Линии приложения реальных сил ${ displaystyle { scriptstyle { vec {F}} _ {1}}}$ и ${ displaystyle scriptstyle { vec {F}} _ {2}}$ на крайнем левом рисунке пересекаются. После векторное сложение выполняется "по месту нахождения ${ displaystyle scriptstyle { vec {F}} _ {1}}$", равнодействующая сила полученное транслируется так, что его линия приложения проходит через общую точку пересечения. Относительно этой точки все крутящие моменты равны нулю, поэтому крутящий момент равнодействующей силы ${ displaystyle scriptstyle { vec {F}} _ {R}}$ равна сумме моментов действительных сил.
2. На рисунке в середине диаграммы показаны две параллельные действительные силы. После сложения вектора »в месте расположения ${ displaystyle scriptstyle { vec {F}} _ {2}}$", результирующая сила переводится в соответствующую линию приложения, где она становится равнодействующей. ${ displaystyle scriptstyle { vec {F}} _ {R}}$. Процедура основана на разложении всех сил на составляющие, для которых линии приложения (бледные пунктирные линии) пересекаются в одной точке (так называемый полюс, произвольно установленный в правой части иллюстрации). Затем аргументы из предыдущего случая применяются к силам и их компонентам, чтобы продемонстрировать отношения крутящего момента.
3. На крайнем правом рисунке показан пара, две равные, но противоположные силы, для которых сумма результирующей силы равна нулю, но они создают чистый крутящий момент ${ Displaystyle scriptstyle tau = Fd}$ куда ${ displaystyle scriptstyle d}$ расстояние между линиями их применения. Это «чистый» крутящий момент, поскольку равнодействующей силы нет.

Связанный вектор

Сила, приложенная к телу, имеет точку приложения. Влияние силы разное для разных точек приложения. По этой причине сила называется связанный вектор, что означает, что он привязан к своей точке приложения.

Силы, приложенные к одной и той же точке, можно сложить, чтобы получить такое же воздействие на тело. Однако силы с разными точками приложения нельзя складывать вместе и поддерживать одинаковое воздействие на тело.

Изменить точку приложения силы просто, введя равные и противоположные силы в двух разных точках приложения, которые создают чистый крутящий момент на теле. Таким образом, все силы, действующие на тело, могут быть перемещены в одну точку приложения с соответствующими крутящими моментами.

Система сил на твердом теле объединяется путем перемещения сил в одну и ту же точку приложения и вычисления соответствующих крутящих моментов. Сумма этих сил и моментов дает результирующую силу-вращающий момент.

Связанный крутящий момент

Если точка р выбирается как точка приложения равнодействующей силы F системы п силы F_я тогда соответствующий крутящий момент Т определяется по формулам

${ displaystyle mathbf {F} = sum _ {i = 1} ^ {n} mathbf {F} _ {i},}$

и

${ displaystyle mathbf {T} = sum _ {i = 1} ^ {n} ( mathbf {R} _ {i} - mathbf {R}) times mathbf {F} _ {i}. }$

Полезно отметить, что точка приложения р результирующей силы может быть где угодно на линии действия F без изменения значения соответствующего крутящего момента. Чтобы увидеть это, добавьте вектор kF к моменту применения р при расчете соответствующего крутящего момента,

${ displaystyle mathbf {T} = sum _ {i = 1} ^ {n} ( mathbf {R} _ {i} - ( mathbf {R} + k mathbf {F})) раз mathbf {F} _ {i}.}$

Правую часть этого уравнения можно разделить на исходную; формула для Т плюс дополнительный член, включающий kF,

${ displaystyle mathbf {T} = sum _ {i = 1} ^ {n} ( mathbf {R} _ {i} - mathbf {R}) times mathbf {F} _ {i} - sum _ {i = 1} ^ {n} k mathbf {F} times mathbf {F} _ {i} = sum _ {i = 1} ^ {n} ( mathbf {R} _ { i} - mathbf {R}) times mathbf {F} _ {i},}$

потому что второй член равен нулю. Чтобы увидеть это уведомление, F это сумма векторов F_я что дает

${ displaystyle sum _ {i = 1} ^ {n} k mathbf {F} times mathbf {F} _ {i} = k mathbf {F} times ( sum _ {i = 1} ^ {п} mathbf {F} _ {i}) = 0,}$

таким образом, значение соответствующего крутящего момента остается неизменным.

Результат без крутящего момента

Полезно подумать, есть ли точка приложения р так что связанный крутящий момент равен нулю. Эта точка определяется свойством

${ displaystyle mathbf {R} times mathbf {F} = sum _ {i = 1} ^ {n} mathbf {R} _ {i} times mathbf {F} _ {i},}$

куда F равнодействующая сила и F_я образуют систему сил.

Обратите внимание, что это уравнение для р имеет решение, только если сумма отдельных крутящих моментов в правой части дает вектор, перпендикулярный F. Таким образом, условие, что система сил имеет равнодействующую без крутящего момента, может быть записано как

${ displaystyle mathbf {F} cdot ( sum _ {i = 1} ^ {n} mathbf {R} _ {i} times mathbf {F} _ {i}) = 0.}$

Если это условие выполнено, то есть точка приложения для результирующей, которая приводит к чистой силе. Если это условие не выполняется, то система сил включает чистый крутящий момент для каждой точки приложения.

Гаечный ключ

Силы и моменты, действующие на твердое тело, можно собрать в пару векторов, называемых гаечный ключ.^[2]Если система сил и моментов имеет результирующую силу F и чистый результирующий крутящий момент Т, то всю систему можно заменить силой F и произвольно расположенная пара, которая дает крутящий момент Т. В общем, если F и Т ортогональны, можно получить радиальный вектор р такой, что ${ Displaystyle mathbf {R} times mathbf {F} = mathbf {T}}$, что означает, что единственная сила F, действующий при вытеснении р, можно заменить систему. Если система работает с нулевым усилием (только крутящий момент), она называется винт и математически формулируется как теория винта.^[3][4]

Результирующая сила и крутящий момент на твердом теле, полученные от системы сил F_я i = 1, ..., n, просто сумма отдельных гаечных ключей W_я, то есть

${ displaystyle { mathsf {W}} = sum _ {i = 1} ^ {n} { mathsf {W}} _ {i} = sum _ {i = 1} ^ {n} ( mathbf {F} _ {i}, mathbf {R} _ {i} times mathbf {F} _ {i}).}$

Обратите внимание, что в случае двух равных, но противоположных сил F и -F действуя в точках А и B соответственно, дает W = (F-F, А×F - B× F) = (0, (А-B)×F). Это показывает, что ключи вида W = (0, Т) можно интерпретировать как чистый крутящий момент.

Рекомендации