WikiDer > Ромбический икосаэдр
| Ромбический икосаэдр | |
|---|---|
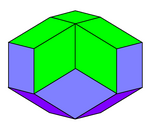 | |
| Тип | зоноэдр |
| Лица | 20 золотые ромбики |
| Края | 40 |
| Вершины | 22 |
| Граней на вершину | 3, 4 и 5 |
| Двойной многогранник | неправильное лицо пятиугольная гиробикупола |
| Симметрия | D5d, [2+,10], (2*5) |
| Характеристики | выпуклый, зоноэдр |
В ромбический икосаэдр это многогранник в форме сплюснутый сфера. Его 20 лиц конгруэнтный золотые ромбики,[1] из которых три, четыре или пять пересекаются в каждой вершине. Он имеет 5 граней (зеленые на первом рисунке), пересекающиеся на каждом из двух полюсов (эти 2 вершины лежат на его оси (5-кратной) симметрии), и 10 граней, следующих за его экватором (2 из их 4 ребер (каждая). лежат на полилинии экватора). Она имеет D5d, [2+, 10], (2 * 5) симметрия, порядок 20.
Несмотря на то, что все его грани совпадают, ромбический икосаэдр не лицо переходный, так как можно различить, находится ли конкретная грань около экватора или полюса, исследуя типы вершин, окружающих эту грань.
Зоноэдр
Ромбический икосаэдр - это зоноэдр, который двойственен к неправильному лицу пятиугольная гиробикупола. Он имеет 5 наборов по 8 параллельных кромок, описываемых как 85 ремни.
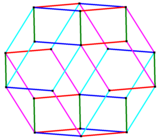 | Ребра ромбического икосаэдра существуют в 5 параллельных наборах, как видно на этой ортогональной проекции каркаса. |
Ромбический икосаэдр образует выпуклую оболочку проекции первой вершины 5-куб до 3-х измерений. 32 вершины 5-куба преобразуются в 22 внешние вершины ромбического икосаэдра, а оставшиеся 10 внутренних вершин образуют пятиугольная антипризма. Таким же образом можно получить Додекаэдр Билинского из 4-куб и ромбический триаконтаэдр из 6-куб.
Связанные многогранники
Ромбический икосаэдр может быть получен из ромбический триаконтаэдр удалив 10 средних граней.
 А ромбический триаконтаэдр как удлиненный ромбический икосаэдр | 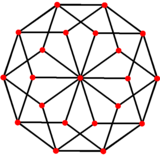 Ромбический икосаэдр разделяет ортогональную проекцию 5-кратной симметрии с ромбический триаконтаэдр |
Рекомендации
- ^ Вайсштейн, Эрик В. «Ромбический Икосаэдр». mathworld.wolfram.com. Получено 2019-12-20.
внешняя ссылка
- Вайсштейн, Эрик В. «Ромбический икосаэдр». MathWorld.
- http://www.georgehart.com/virtual-polyhedra/zonohedra-info.html
| Этот многогранник-связанная статья является заглушка. Вы можете помочь Википедии расширяя это. |