WikiDer > ТАК (10)

Эта статья поднимает множество проблем. Пожалуйста помоги Улучши это или обсудите эти вопросы на страница обсуждения. (Узнайте, как и когда удалить эти сообщения-шаблоны) Эта статья требует внимания специалиста по физике. Пожалуйста, добавьте причина или разговаривать в этот шаблон, чтобы объяснить проблему со статьей. ВикиПроект Физика может помочь нанять эксперта. (Июль 2009 г.) Эта статья нужны дополнительные цитаты для проверка. Пожалуйста помоги улучшить эту статью к добавление цитат в надежные источники. Материал, не полученный от источника, может быть оспорен и удален Найдите источники: «СО (10)» – Новости · газеты · книги · ученый · JSTOR (Январь 2008 г.) (Узнайте, как и когда удалить этот шаблон сообщения) Эта статья может быть слишком техническим для большинства читателей, чтобы понять. Пожалуйста помогите улучшить это к сделать понятным для неспециалистов, не снимая технических деталей. (Сентябрь 2010 г.) (Узнайте, как и когда удалить этот шаблон сообщения) (Узнайте, как и когда удалить этот шаблон сообщения)

Образец слабый изоспин, W, более слабый изоспин, W ', сильные g3 и g8, и барион минус лептон, B, заряды для частиц в модели SO (10), повернутые, чтобы показать вложение Георги – Глэшоу модель и Стандартная модель, с электрическим зарядом примерно по вертикали. Помимо частиц Стандартной модели, теория включает 30 цветных X-бозонов, отвечающих за распад протона, и два W 'бозона.

Схема зарядов для частиц в модели SO (10), повернутая, чтобы показать встраивание в E6.

В физика элементарных частиц, ТАК (10) относится к теория великого единства (GUT) на основе вращательная группа Вращение (10). Сокращенное название SO (10) условно^[1] среди физиков, и происходит от Группа Ли SO (10), который является специальная ортогональная группа то есть двойное покрытие по Спину (10).

История

Перед SU (5) теория позади Георги – Глэшоу модель^[2], Харальд Фрич и Питер Минковски, и независимо Говард Джорджи, обнаружил, что все содержимое материала объединено в единое представление, спинориальный 16 SO (10). Однако стоит отметить, что Георги нашел теорию SO (10) всего за несколько часов до того, как нашел SU (5) в конце 1973 года.^[3]

Важные подгруппы

Он имеет правила ветвления в [SU (5) × U (1)_χ]/Z₅.

${ displaystyle 45 rightarrow 24_ {0} oplus 10 _ {- 4} oplus { overline {10}} _ {4} oplus 1_ {0}}$

${ displaystyle 16 rightarrow 10_ {1} oplus { bar {5}} _ {- 3} oplus 1_ {5}}$

${ displaystyle 10 rightarrow 5 _ {- 2} oplus { bar {5}} _ {2}.}$

Если сверхзаряд содержится в SU (5), это обычная Георги – Глэшоу модель, с 16 как полями материи, 10 как электрослабое поле Хиггса и 24 внутри 45 как поле Хиггса GUT. В сверхпотенциал затем может включать перенормируемый условия формы Тр(45 ⋅ 45); Тр(45 ⋅ 45 ⋅ 45); 10 ⋅ 45 ⋅ 10, 10 ⋅ 16 * ⋅ 16 и 16 * ⋅ 16. Первые три несут ответственность перед калибровочная симметрия ломаются при низких энергиях и дают Хиггс массы, а последние два дают массы частиц материи и их Муфты Юкава к Хиггсу.

Существует еще одно возможное ветвление, при котором гиперзаряд представляет собой линейную комбинацию генератора SU (5) и χ. Это известно как перевернутый SU (5).

Другой важной подгруппой является либо [SU (4) × SU (2)_L × СУ (2)_р]/Z₂ или же Z₂ ⋊ [СУ (4) × СУ (2)_L × СУ (2)_р]/Z₂ в зависимости от того, лево-правая симметрия сломан, давая Модель Пати – Салам, чье правило ветвления

${ Displaystyle 45 rightarrow (15,1,1) oplus (6,2,2) oplus (1,3,1) oplus (1,1,3)}$

${ displaystyle 16 rightarrow (4,2,1) oplus ({ bar {4}}, 1,2).}$

Спонтанное нарушение симметрии

Нарушение симметрии SO (10) обычно выполняется комбинацией ((a 45_ЧАС ИЛИ 54_ЧАС) И ((a 16_ЧАС И ${ displaystyle { overline {16}} _ {H}}$) ИЛИ (a 126_ЧАС И ${ displaystyle { overline {126}} _ {H}}$)) ).

Допустим, мы выбираем 54_ЧАС. Когда это поле Хиггса приобретает шкалу GUT VEV, имеем нарушение симметрии на Z₂ ⋊ [СУ (4) × СУ (2)_L × СУ (2)_р]/Z₂, т.е. Модель Пати – Салам с Z₂ лево-правая симметрия.

Если у нас есть 45_ЧАС вместо этого это поле Хиггса может получить любую VEV в двумерном подпространстве, не нарушая стандартную модель. В зависимости от направления этой линейной комбинации мы можем нарушить симметрию до SU (5) × U (1), Георги – Глэшоу модель с U (1) (diag (1,1,1,1,1, -1, -1, -1, -1, -1)), перевернутый SU (5) (diag (1,1,1, -1, -1, -1, -1, -1,1,1)), SU (4) × SU (2) × U (1) (diag (0,0 , 0,1,1,0,0,0, -1, -1)) минимальная лево-правая модель (diag (1,1,1,0,0, -1, -1, -1,0,0)) или SU (3) × SU (2) × U (1) × U (1) для любого другого ненулевой ВЭВ.

Выбор diag (1,1,1,0,0, -1, -1, -1,0,0) называется Механизм Димопулоса-Вильчека он же «отсутствующий механизм VEV», и он пропорционален B − L.

Выбор из 16_ЧАС и ${ displaystyle { overline {16}} _ {H}}$ разбивает калибровочную группу на SU Джорджи – Глэшоу (5). То же самое относится и к выбору 126_ЧАС и ${ displaystyle { overline {126}} _ {H}}$.

Это комбинация ОБЕИ 45/54 и 16 /${ displaystyle { overline {16}}}$ или 126 /${ displaystyle { overline {126}}}$ что разбивает SO (10) на Стандартная модель.

Электрослабый Хиггс и проблема дублет-триплетного расщепления

Электрослабые дублеты Хиггса происходят от SO (10) 10_ЧАС. К сожалению, в этой же 10 тройке тоже есть. Массы дублетов должны быть стабилизированы в электрослабом масштабе, который на много порядков меньше, чем масштаб GUT, тогда как триплеты должны быть действительно тяжелыми, чтобы предотвратить опосредованное триплетом протон распадается. Видеть задача дублет-триплетного расщепления.

Среди решений для этого - механизм Димопулоса-Вильчека или выбор diag (0,0,0,1,1,0,0,0, -1, -1) из <45>. К сожалению, это нестабильно, если 16 /${ displaystyle { overline {16}}}$ или 126 /${ displaystyle { overline {126}}}$ сектор взаимодействует с сектором 45.^[4]

Содержание

Иметь значение

Представления материи бывают в трех копиях (поколениях) из 16 представлений. В Юкава муфта 10 лет_ЧАС 16_ж 16_ж. Сюда входит правое нейтрино. Можно включить три копии синглет представления φ и соединение Юкавы ${ displaystyle <{ overline {16}} _ {H}> 16_ {f} phi}$ («механизм двойных качелей»); или же добавьте взаимодействие Юкавы ${ displaystyle <{ overline {126}} _ {H}> 16_ {f} 16_ {f}}$ или добавить неперенормируемый связь ${ displaystyle <{ overline {16}} _ {H}> <{ overline {16}} _ {H}> 16_ {f} 16_ {f}}$. Видеть механизм качелей.

16_ж поля разветвляются на [SU (5) × U (1)_χ]/Z₅ и SU (4) × SU (2)_L × СУ (2)_р в качестве

${ displaystyle 16 rightarrow 10_ {1} oplus { bar {5}} _ {- 3} oplus 1_ {5}}$

${ displaystyle 16 rightarrow (4,2,1) oplus ({ bar {4}}, 1,2).}$

Калибровочные поля

Поле 45 разветвляется на [SU (5) × U (1)_χ]/Z₅ и SU (4) × SU (2)_L × СУ (2)_р в качестве

${ displaystyle 45 rightarrow 24_ {0} oplus 10 _ {- 4} oplus { overline {10}} _ {4} oplus 1_ {0}}$

${ Displaystyle 45 rightarrow (15,1,1) oplus (6,2,2) oplus (1,3,1) oplus (1,1,3)}$

и к стандартной модели [SU (3)_C × СУ (2)_L × U (1)_Y]/Z₆ в качестве

${ displaystyle { begin {align} 45 rightarrow & (8,1) _ {0} oplus (1,3) _ {0} oplus (1,1) _ {0} oplus & ( 3,2) _ {- { frac {5} {6}}} oplus ({ bar {3}}, 2) _ { frac {5} {6}} oplus & (3, 1) _ { frac {2} {3}} oplus ({ bar {3}}, 1) _ {- { frac {2} {3}}} oplus (1,1) _ {1 } oplus (1,1) _ {- 1} oplus (1,1) _ {0} oplus & (3,2) _ { frac {1} {6}} oplus ({ бар {3}}, 2) _ {- { frac {1} {6}}}. конец {выровнено}}}$

Четыре линии - это SU (3)_C, СУ (2)_L, и U (1)_{B − L} бозоны; в SU (5) лептокварки, которые не мутируют X заряд; в Пати-Салам лептокварки и SU (2)_р бозоны; и новые лептокварки SO (10). (Стандарт электрослабый U (1)_Y является линейной комбинацией (1,1)₀ бозоны.)

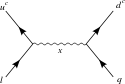
Распад протона

• Эти рисунки относятся к X-бозоны и Бозоны Хиггса.
• 

  Распад протона размерности 6 опосредован Икс бозон ${ displaystyle (3,2) _ {- { frac {5} {6}}}}$ в SU (5) GUT

• 

  Распад протона размерности 6 опосредован Икс бозон ${ displaystyle (3,2) _ { frac {1} {6}}}$ в перевернутом SU (5) GUT

Обратите внимание, что SO (10) содержит как SU Джорджи – Глэшоу (5), так и перевернутую SU (5).

Аномалия без локальных и глобальных аномалий

Давно известно, что модель SO (10) свободна от всех пертурбативных локальных аномалий, вычисляемых с помощью диаграмм Фейнмана. Однако только в 2018 году станет ясно, что модель SO (10) также свободна от всех непертурбативные глобальные аномалии на неспиновых многообразиях - важное правило для подтверждения согласованности ТАК (10) теория великого объединения с калибровочной группой Spin (10) и киральными фермионами в 16-мерных спинорных представлениях, определенных на неспиновые многообразия.^[5][6]

Смотрите также

• Перевернутая ТАК (10)

Примечания