WikiDer > Малый сложный ромбикосододекаэдр
| Малый сложный ромбикосододекаэдр | |
|---|---|
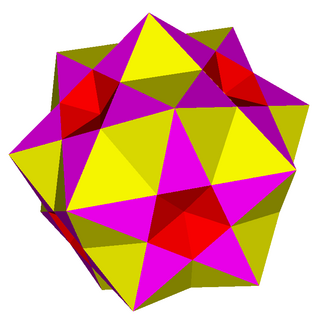 | |
| Тип | Равномерный звездный многогранник |
| Элементы | F = 62, E = 120 (60x2) V = 20 (χ = -38) |
| Лица по сторонам | 20{3}+12{5/2}+30{4} |
| Символ Wythoff | 5/2 3 | 2 |
| Группа симметрии | Ih, [5,3], * 532 |
| Указатель ссылок | U-, C-, W- |
| Двойной многогранник | Мелкий сложный ромбикосидодекакрон |
| Фигура вершины |  3(3.4.5/2.4) |
| Акроним Bowers | Sicdatrid |
В геометрии малый сложный ромбикосододекаэдр (также известный как малый сложный дитригональный ромбикосододекаэдр) это выродиться равномерный звездный многогранник. Имеет 62 лица (20 треугольники, 12 пентаграммы и 30 квадраты), 120 (удвоенных) ребер и 20 вершин. Все ребра удваиваются (что делает его вырожденным), разделяют 4 грани, но считаются двумя перекрывающимися ребрами как топологический многогранник.
Его можно построить из вершины фигуры 3 (5/2.4.3.4), что делает его также скошенный большой икосаэдр. Цифра "3" перед этой фигурой вершины означает, что каждая вершина в этом вырожденном многограннике фактически состоит из трех совпадение вершины. Также может быть Символ Шлефли rr {5⁄2, 3} или t0,2{5⁄2,3}.
Как соединение
Это можно рассматривать как соединение из малый дитригональный икосододекаэдр, U30, а соединение пяти кубиков. Это также огранка из додекаэдр.
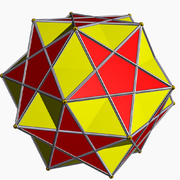 | 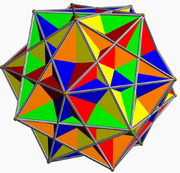 |  |
| Малый дитригональный икосододекаэдр | Соединение пяти кубиков | Соединение |
Как песня
Его также можно рассматривать как песня из большой икосаэдр (или, что то же самое, большой звездчатый додекаэдр).
| (p q 2) | Фонд. треугольник | Родитель | Усеченный | Исправленный | Bitruncated | Двунаправленный (двойной) | Собранный | Усеченный (Усеченный) | Курносый |
|---|---|---|---|---|---|---|---|---|---|
| Символ Wythoff | q | п 2 | 2 q | п | 2 | p q | 2 п | q | p | q 2 | p q | 2 | p q 2 | | | p q 2 | |
| Символ Шлефли | т0{p, q} | т0,1{p, q} | т1{p, q} | т1,2{p, q} | т2{p, q} | т0,2{p, q} | т0,1,2{p, q} | s {p, q} | |
| Диаграмма Кокстера – Дынкина | |||||||||
| Фигура вершины | пq | q.2p.2p | p.q.p.q | p.2q.2q | qп | стр.4.q.4 | 4.2p.2q | 3.3.p.3.q | |
| Икосаэдр (5⁄2 3 2) |  {3,5⁄2} |  5⁄2.6.6 |  (3.5⁄2)2 |  3.10⁄2.10⁄2 |  {5⁄2,3} |  3.4.5⁄2.4 |  4.10⁄2.6 |  3.3.3.3.5⁄2 |
Связанные вырожденные однородные многогранники
Два других вырожденных однородных многогранника также являются фасетками додекаэдра. Они сложный ромбидодекадодекаэдр (соединение дитригональный додекадодекаэдр и соединение пяти кубиков) с вершиной фигуры (5⁄3.4.5.4) / 3 и большой сложный ромбикосододекаэдр (соединение большой дитригональный икосододекаэдр и соединение пяти кубиков) с вершиной фигуры (5⁄4.4.3⁄2.4) / 3. У всех трех вырожденных равномерных многогранников каждая вершина фактически является тремя совпадающими вершинами, а каждое ребро фактически является двумя совпадающими ребрами.
Все они могут быть построены песнопение правильные многогранники. Сложному ромбидодекадодекаэдру можно присвоить символ Шлефли rr {5⁄3, 5} или t0,2{5⁄3, 5}, в то время как большому сложному ромбикосододекаэдру можно присвоить символ Шлефли rr {5⁄4,3⁄2} или t0,2{5⁄4,3⁄2}.
| Скошенный многогранник | 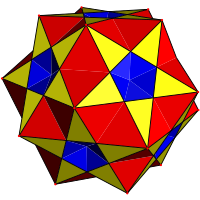 Малый сложный ромбикосододекаэдр | 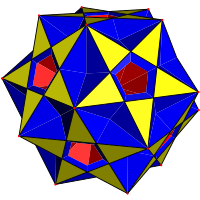 Сложный ромбидодекадодекаэдр | 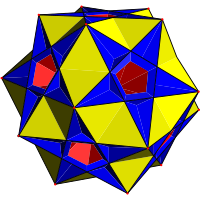 Большой сложный ромбикосододекаэдр | |||
|---|---|---|---|---|---|---|
| Связанный многогранник |  Большой икосаэдр |  Большой звездчатый додекаэдр |  Большой додекаэдр | 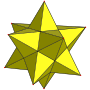 Малый звездчатый додекаэдр | 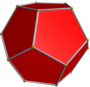 Правильный додекаэдр |  Правильный икосаэдр |
Смотрите также
- Малый сложный икосододекаэдр
- Большой сложный икосододекаэдр
- Сложный ромбидодекадодекаэдр
- Большой сложный ромбикосододекаэдр
использованная литература
- Клитцинг, Ричард. "Трехмерные однородные многогранники sicdatrid".
- Клитцинг, Ричард. "Трехмерные однородные многогранники каддитрадид".
- Клитцинг, Ричард. "Трехмерные однородные многогранники gicdatrid".