WikiDer > Тетрация

Раскраска домена из голоморфный тетрация ${ displaystyle {} ^ {z} e}$, с участием оттенок представляя функцию аргумент и яркость представляющий величину

${ Displaystyle {} ^ {п} х}$, за п = 2, 3, 4, ..., демонстрируя сходимость к бесконечно повторяющейся экспоненте между двумя точками

В математика, тетрация (или же гипер-4) является операция на основе повторяется, или повторяется, возведение в степень. Это следующий гипероперация после возведение в степень, но прежде пентация. Слово было придумано Рубен Луи Гудштейн из тетра- (четыре) и итерация.

В соответствии с определением повторного возведения в степень, обозначение ${ Displaystyle {^ {п} а}}$ средства ${ Displaystyle {а ^ {а ^ { cdot ^ { cdot ^ {а}}}}}}$, куда п копии а повторяются через возведение в степень справа налево, т.е. применение возведения в степень ${ displaystyle n-1}$ раз. п называется "высотой" функции, а а называется «основанием», аналогично возведению в степень. Это будет читаться как " п-я тетрация а".

Тетрация также определяется рекурсивно как

${ displaystyle {^ {n} a}: = { begin {case} 1 & { text {if}} n = 0 a ^ { left (^ {(n-1)} a right)} & { text {if}} n> 0 end {case}}}$,

с учетом попыток расширить тетрацию до не натуральных чисел, таких как действительные и комплексные числа.

Две инверсии тетрации называются супер-корень и суперлогарифм, аналогично корню n-й степени и логарифмическим функциям. Ни одна из трех функций не элементарный.

Тетрация используется для запись очень больших чисел.

Вступление

Первые четыре гипероперации показаны здесь, причем тетрация считается четвертой в серии. В унарная операция преемственность, определяется как ${ Displaystyle а '= а + 1}$, считается нулевой операцией.

1. Добавление

   ${ Displaystyle а + п = а + underbrace {1 + 1 + cdots +1} _ {п}}$

   п копии 1 добавлены в а.

2. Умножение

   ${ Displaystyle а раз п = underbrace {а + а + cdots + а} _ {п}}$

   п копии а объединены сложением.

3. Возведение в степень

   ${ Displaystyle а ^ {п} = underbrace {а раз а раз cdots раз а} _ {п}}$

   п копии а объединены путем умножения.

4. Тетрация

   ${ displaystyle {^ {n} a} = underbrace {a ^ {a ^ { cdot ^ { cdot ^ {a}}}}} _ {n}}$

   п копии а в сочетании с возведением в степень справа налево.^[1]

Наследование, (а ' = а + 1), это самая простая операция; а сложение (а + п) является основной операцией, для сложения натуральных чисел ее можно рассматривать как последовательную последовательность п преемники а; умножение (а × п) также является основной операцией, хотя для натуральных чисел ее аналогично можно рассматривать как связанное сложение, включающее п количество а. Возведение в степень можно рассматривать как связанное умножение, включающее п количество а и тетрация (${ Displaystyle ^ {п} а !}$) как связанная сила, включающая п числа а. Каждая из вышеперечисленных операций определяется повторением предыдущей;^[2] однако, в отличие от предшествующих операций, тетрация не является элементарная функция.

Параметр а называется основание, а параметр п можно назвать рост. В исходном определении тетрации параметр высоты должен быть натуральным числом; например, было бы нелогично сказать, что «три подняли к себе отрицание пять раз» или «четыре подняли к себе половину времени». Однако так же, как сложение, умножение и возведение в степень могут быть определены способами, позволяющими расширять действительные и комплексные числа, было предпринято несколько попыток обобщить тетрацию на отрицательные числа, действительные числа и комплексные числа. Один из таких способов - использовать рекурсивное определение тетрации; для любого положительного настоящий ${ displaystyle a> 0}$ и неотрицательный целое число ${ Displaystyle п geq 0}$, мы можем определить ${ Displaystyle , ! {^ {п} а}}$ рекурсивно как:^[2]

${ displaystyle {^ {n} a}: = { begin {case} 1 & { text {if}} n = 0 a ^ { left (^ {(n-1)} a right)} & { text {if}} n> 0 end {case}}}$

Рекурсивное определение эквивалентно повторному возведению в степень для естественный высоты; однако это определение допускает расширение на другие высоты, такие как ${ displaystyle ^ {0} а}$, ${ displaystyle ^ {- 1} а}$, и ${ Displaystyle ^ {я} а}$ а также - многие из этих расширений являются областями активных исследований.

Терминология

Существует множество терминов для обозначения тетрации, каждый из которых имеет определенную логику, но некоторые из них не стали широко использоваться по той или иной причине. Вот сравнение каждого термина с его обоснованием и контробоснованием.

• Период, термин тетрация, представленный Гудштейном в его статье 1947 г. Трансфинитные порядковые числа в рекурсивной теории чисел^[3] (обобщая рекурсивное базовое представление, используемое в Теорема Гудштейна использовать более высокие операции), завоевала господство. Он также был популяризирован в Руди Ракерс Бесконечность и разум.
• Период, термин сверхэкспоненциация был опубликован Бромером в его статье Суперэкспоненциация в 1987 г.^[4] Ранее его использовал Эд Нельсон в своей книге «Предикативная арифметика», Princeton University Press, 1986.
• Период, термин сверхмощность^[5] это естественное сочетание гипер и мощность, что точно описывает тетрацию. Проблема заключается в значении гипер с уважением к гипероперация последовательность. При рассмотрении гиперопераций термин гипер относится ко всем рангам, а термин супер относится к рангу 4 или тетрации. Итак, исходя из этих соображений сверхмощность вводит в заблуждение, так как относится только к тетрации.
• Период, термин силовая башня^[6] иногда используется в форме "силовая башня порядка п" за ${ Displaystyle { на вершине {}} {{ underbrace {a ^ {a ^ { cdot ^ { cdot ^ {a}}}}}} на вершине n}}$. Однако это неправильное название, потому что тетрация не может быть выражена с помощью повторения. мощность функций (см. выше), поскольку это итеративная экспоненциальный функция.

Отчасти из-за общей терминологии и аналогичных условная символика, тетрацию часто путают с тесно связанными функциями и выражениями. Вот несколько связанных терминов:

Термины, относящиеся к тетрации

Терминология	Форма
Тетрация	${ Displaystyle а ^ {а ^ { cdot ^ { cdot ^ {а ^ {а}}}}}}$
Итерированные экспоненты	${ Displaystyle а ^ {а ^ { cdot ^ { cdot ^ {а ^ {х}}}}}}$
Вложенные экспоненты (также башни)	${ Displaystyle а_ {1} ^ {а_ {2} ^ { cdot ^ { cdot ^ {а_ {п}}}}}}$
Бесконечные экспоненты (также башни)	${ Displaystyle а_ {1} ^ {а_ {2} ^ {а_ {3} ^ { cdot ^ { cdot ^ { cdot}}}}}}$

В первых двух выражениях а это основание, а количество раз а появляется рост (добавьте один для Икс). В третьем выражении п это рост, но каждая из баз разная.

Следует проявлять осторожность при обращении к повторяющимся экспонентам, так как выражения этой формы обычно называют повторным возведением в степень, что неоднозначно, поскольку это может означать повторяется полномочия или повторяется экспоненты.

Обозначение

Есть много разных стилей обозначений, которые можно использовать для выражения тетрации. Некоторые обозначения могут также использоваться для описания других гипероперации, в то время как некоторые ограничиваются тетрацией и не имеют немедленного расширения.

Стили обозначений для тетрации

Имя	Форма	Описание
Обозначения Руди Ракера	${ displaystyle , {} ^ {n} а}$	Используется Маурером [1901] и Гудстейном [1947]; Руди Ракеркнига Бесконечность и разум популяризировал обозначения.[nb 1]
Обозначение Кнута со стрелкой вверх	${ displaystyle a { uparrow uparrow} п}$	Позволяет расширить, добавив больше стрелок или, что еще важнее, указав стрелку.
Обозначение стрелок Конвея	${ Displaystyle а rightarrow п rightarrow 2}$	Позволяет расширять за счет увеличения числа 2 (эквивалент вышеуказанных расширений), но также, что еще более эффективно, за счет удлинения цепочки
Функция Аккермана	${ displaystyle {} ^ {n} 2 = operatorname {A} (4, n-3) +3}$	Позволяет особый случай ${ displaystyle a = 2}$ быть записанным в терминах функции Аккермана.
Итерированная экспоненциальная запись	${ Displaystyle ехр _ {а} ^ {п} (1)}$	Позволяет простое расширение до повторяющихся экспонент от начальных значений, отличных от 1.
Обозначения Хушмана[7]	${ displaystyle { begin {align} & operatorname {uxp} _ {a} n [2pt] & a ^ { frac {n} {}} end {align}}}$	Используется М. Х. Хушмандом [2006].
Гипероперация обозначения	${ displaystyle { begin {align} & a [4] n [2pt] & H_ {4} (a, n) end {выравнивается}}}$	Позволяет расширить за счет увеличения числа 4; это дает семье гипероперации.
Обозначение двойной вставки	а ^^ п	Поскольку стрелка вверх используется так же, как и курсор (^) тетрация может быть записана как (^^); удобно для ASCII.

В одной из приведенных выше обозначений используется итеративная экспоненциальная запись; в целом это определяется следующим образом:

${ Displaystyle ехр _ {а} ^ {п} (х) = а ^ {а ^ { cdot ^ { cdot ^ {а ^ {х}}}}}}$ с п ас.

Для повторяющихся экспонент не так много обозначений, но вот несколько:

Стили обозначений для повторяющихся экспонент

Имя	Форма	Описание
Стандартные обозначения	${ Displaystyle ехр _ {а} ^ {п} (х)}$	Эйлер придумал обозначение ${ Displaystyle ехр _ {а} (х) = а ^ {х}}$, и обозначение итераций ${ Displaystyle е ^ {п} (х)}$ существует примерно столько же.
Обозначение Кнута со стрелкой вверх	${ Displaystyle (а { вверх}) ^ {п} (х)}$	Позволяет использовать сверхдержавы и суперэкспоненциальную функцию за счет увеличения количества стрелок; используется в статье о большие числа.
Текстовое обозначение	exp_а^п (х)	Основано на стандартных обозначениях; удобно для ASCII.
Обозначение J	Икс^^:(п-1)Икс	Повторяет возведение в степень. Видеть J (язык программирования)[8]

Примеры

Из-за чрезвычайно быстрого роста тетрации большинство значений в следующей таблице слишком велики для записи в научных обозначениях. В этих случаях используется итеративная экспоненциальная запись, чтобы выразить их в базе 10. Значения, содержащие десятичную точку, являются приблизительными.

Примеры тетрации

${ displaystyle x}$	${ displaystyle {} ^ {2} x}$	${ displaystyle {} ^ {3} x}$	${ displaystyle {} ^ {4} x}$	${ displaystyle {} ^ {5} x}$
1	1	1	1	1
2	4	16	65,536	265,536 или (2,0035 × 1019,728)
3	27	7,625,597,484,987	${ Displaystyle ехр _ {10} ^ {3} (1.09902)}$ (3.68 × 1012 цифры)	${ Displaystyle ехр _ {10} ^ {4} (1.09902)}$
4	256	1.34078 × 10154	${ displaystyle exp _ {10} ^ {3} (2,18726)}$ (8.1 × 10153 цифры)	${ displaystyle exp _ {10} ^ {4} (2,18726)}$
5	3,125	1.91101 × 102,184	${ Displaystyle ехр _ {10} ^ {3} (3,33928)}$ (1.3 × 102,184 цифры)	${ displaystyle exp _ {10} ^ {4} (3,33928)}$
6	46,656	2.65912 × 1036,305	${ displaystyle exp _ {10} ^ {3} (4,55997)}$ (2.1 × 1036,305 цифры)	${ displaystyle exp _ {10} ^ {4} (4.55997)}$
7	823,543	3.75982 × 10695,974	${ displaystyle exp _ {10} ^ {3} (5,84259)}$ (3.2 × 10695,974 цифры)	${ displaystyle exp _ {10} ^ {4} (5,84259)}$
8	16,777,216	6.01452 × 1015,151,335	${ displaystyle exp _ {10} ^ {3} (7.18045)}$ (5.4 × 1015,151,335 цифры)	${ displaystyle exp _ {10} ^ {4} (7.18045)}$
9	387,420,489	4.28125 × 10369,693,099	${ displaystyle exp _ {10} ^ {3} (8,56784)}$ (4.1 × 10369,693,099 цифры)	${ displaystyle exp _ {10} ^ {4} (8,56784)}$
10	10,000,000,000	1010,000,000,000	${ Displaystyle ехр _ {10} ^ {3} (10)}$ (1010,000,000,000 + 1 цифра)	${ Displaystyle ехр _ {10} ^ {4} (10)}$

Характеристики

У тетрации есть несколько свойств, похожих на возведение в степень, а также свойства, которые являются специфическими для операции и теряются или приобретаются в результате возведения в степень. Поскольку возведение в степень не ездить, правила произведения и мощности не имеют аналога с тетрацией; заявления ${ textstyle {} ^ {a} left ({} ^ {b} x right) = left ({} ^ {ab} x right)}$ и ${ textstyle {} ^ {a} left (xy right) = {} ^ {a} x {} ^ {a} y}$ не обязательно верны для всех случаев.^[9]

Однако тетрация имеет другое свойство, в котором ${ textstyle {} ^ {a} x = x ^ { left ({} ^ {a-1} x right)}}$. Этот факт наиболее наглядно демонстрируется с помощью рекурсивного определения. Из этого свойства следует доказательство того, что ${ displaystyle left ({} ^ {b} a right) ^ { left ({} ^ {c} a right)} = left ({} ^ {c + 1} a right) ^ { left ({} ^ {b-1} a right)}}$, что позволяет переключать б и c в некоторых уравнениях. Доказательство выглядит следующим образом:

${ displaystyle { begin {align} & left ({} ^ {b} a right) ^ { left ({} ^ {c} a right)} = {} & left (a ^ {{} ^ {b-1} a} right) ^ { left ({} ^ {c} a right)} = {} & a ^ { left ({} ^ {b-1} a right) left ({} ^ {c} a right)} = {} & a ^ { left ({} ^ {c} a right) left ({} ^ {b-1} a right)} = {} & left ({} ^ {c + 1} a right) ^ { left ({} ^ {b-1} a right)} end {выравнивается}}}$

Когда число Икс и 10 соток совмещать, можно вычислить последний м десятичные цифры ${ Displaystyle , ! ^ {а} х}$ с помощью Теорема Эйлера, для любого целого числа м.

Направление оценки

При оценке тетрации, выраженной как «башня возведения в степень», последовательное возведение в степень выполняется сначала на самом глубоком уровне (в обозначениях, на вершине).^[1] Например:

${ Displaystyle , ! ^ {4} 2 = 2 ^ {2 ^ {2 ^ {2}}} = 2 ^ { left (2 ^ { left (2 ^ {2} right)} right)} = 2 ^ { left (2 ^ {4} right)} = 2 ^ {16} = 65, ! 536}$

Этот порядок важен, потому что возведение в степень не ассоциативный, и вычисляя выражение в противоположном порядок приведет к другому ответу:

${ Displaystyle , ! 2 ^ {2 ^ {2 ^ {2}}} neq left ({ left (2 ^ {2} right)} ^ {2} right) ^ {2} = 4 ^ {2 cdot 2} = 256}$

Оценка выражения слева направо считается менее интересной; оценка слева направо, любое выражение ${ Displaystyle ^ {п} а !}$ можно упростить до ${ Displaystyle а ^ { влево (а ^ {п-1} вправо)} ! !}$.^[10] Из-за этого башни нужно оценивать справа налево (или сверху вниз). Программисты называют этот выбор правоассоциативный.

Расширения

Тетрацию можно расширить двумя способами; в уравнении ${ Displaystyle ^ {п} а !}$, как база а и высота п можно обобщить, используя определение и свойства тетрации. Хотя основание и высота могут быть расширены за пределы неотрицательных целых чисел на разные домены, включая ${ displaystyle {^ {n} 0}}$, сложные функции, такие как ${ displaystyle {} ^ {n} я}$, и высоты бесконечных п, более ограниченные свойства тетрации снижают возможность продления тетрации.

Продление домена для баз

Базовый ноль

Экспоненциальный ${ displaystyle 0 ^ {0}}$ не определяется последовательно. Таким образом, тетрации ${ displaystyle , {^ {n} 0}}$ не определены четко формулой, приведенной ранее. Однако, ${ displaystyle lim _ {x rightarrow 0} {} ^ {n} x}$ хорошо определено и существует:^[11]

${ displaystyle lim _ {x rightarrow 0} {} ^ {n} x = { begin {cases} 1, & n { text {even}} 0, & n { text {odd}} end {случаи}}}$

Таким образом, мы могли последовательно определить ${ displaystyle {} ^ {n} 0 = lim _ {x rightarrow 0} {} ^ {n} x}$. Это аналогично определению ${ displaystyle 0 ^ {0} = 1}$.

В рамках этого расширения ${ displaystyle {} ^ {0} 0 = 1}$, так что правило ${ displaystyle {^ {0} a} = 1}$ из исходного определения все еще в силе.

Комплексные базы

Тетрация по периоду

Тетрация путем побега

С сложные числа может быть возведен в степень, тетрация может применяться к базы формы z = а + би (куда а и б настоящие). Например, в ^пz с z = я, тетрация достигается за счет использования главный филиал натурального логарифма; с помощью Формула Эйлера получаем соотношение:

${ displaystyle i ^ {a + bi} = e ^ {{ frac {1} {2}} { pi i} (a + bi)} = e ^ {- { frac {1} {2}} { pi b}} left ( cos { frac { pi a} {2}} + i sin { frac { pi a} {2}} right)}$

Это предлагает рекурсивное определение для ^п+1я = а ' + b′i учитывая любые ^пя = а + би:

${ displaystyle { begin {align} a '& = e ^ {- { frac {1} {2}} { pi b}} cos { frac { pi a} {2}} [ 2pt] b '& = e ^ {- { frac {1} {2}} { pi b}} sin { frac { pi a} {2}} end {выровнено}}}$

Можно получить следующие приблизительные значения:

Значения тетрации сложных оснований

${ textstyle {} ^ {п} я}$	Приблизительное значение
${ textstyle {} ^ {1} я = я}$	я
${ textstyle {} ^ {2} я = я ^ { влево ({} ^ {1} я вправо)}}$	0.2079
${ textstyle {} ^ {3} я = я ^ { влево ({} ^ {2} я вправо)}}$	0.9472 + 0.3208я
${ textstyle {} ^ {4} я = я ^ { влево ({} ^ {3} я вправо)}}$	0.0501 + 0.6021я
${ textstyle {} ^ {5} я = я ^ { влево ({} ^ {4} я вправо)}}$	0.3872 + 0.0305я
${ textstyle {} ^ {6} я = я ^ { влево ({} ^ {5} я вправо)}}$	0.7823 + 0.5446я
${ textstyle {} ^ {7} я = я ^ { влево ({} ^ {6} я вправо)}}$	0.1426 + 0.4005я
${ textstyle {} ^ {8} я = я ^ { влево ({} ^ {7} я вправо)}}$	0.5198 + 0.1184я
${ textstyle {} ^ {9} я = я ^ { влево ({} ^ {8} я вправо)}}$	0.5686 + 0.6051я

Решение обратной зависимости, как и в предыдущем разделе, дает ожидаемое ⁰я = 1 и ⁻¹я = 0, с отрицательными значениями п давая бесконечные результаты на мнимой оси. Находится в комплексная плоскость, вся последовательность закручивается по спирали до предела 0.4383 + 0.3606я, которое можно интерпретировать как значение, где п бесконечно.

Такие последовательности тетраций изучаются со времен Эйлера, но плохо изучены из-за их хаотического поведения. Исторически сложилось так, что большинство опубликованных исследований было сосредоточено на сходимости бесконечно повторяющейся экспоненциальной функции. Нынешним исследованиям в значительной степени способствовало появление мощных компьютеров с фрактал и программное обеспечение для символьной математики. Многое из того, что известно о тетрации, получено из общих знаний о сложной динамике и конкретных исследований экспоненциальной карты.^{[нужна цитата]}

Расширения домена на разную высоту

Бесконечные высоты

${ displaystyle textstyle lim _ {n rightarrow infty} {} ^ {n} x}$ бесконечно итерированной экспоненты сходится для базисов ${ displaystyle textstyle left (e ^ {- 1} right) ^ {e} leq x leq e ^ { left (e ^ {- 1} right)}}$

Функция ${ displaystyle left | { frac { mathrm {W} (- ln {z})} {- ln {z}}} right |}$ на комплексной плоскости, показывая действительную бесконечно повторяемую экспоненциальную функцию (черная кривая)

Тетрация может быть расширена до бесконечный высоты;^[12] т.е. наверняка а и п ценности в ${ displaystyle {} ^ {n} а}$, существует хорошо определенный результат для бесконечного п. Это связано с тем, что для оснований в определенном интервале тетрация сходится к конечному значению, поскольку высота стремится к бесконечность. Например, ${ displaystyle { sqrt {2}} ^ {{ sqrt {2}} ^ {{ sqrt {2}} ^ { cdot ^ { cdot ^ { cdot}}}}}}$ сходится к 2, и поэтому можно сказать, что он равен 2. Тенденцию к 2 можно увидеть, оценив небольшую конечную башню:

${ displaystyle { begin {align} { sqrt {2}} ^ {{ sqrt {2}} ^ {{ sqrt {2}} ^ {{ sqrt {2}} ^ {{ sqrt {2}) }} ^ {1.414}}}}} & приблизительно { sqrt {2}} ^ {{ sqrt {2}} ^ {{ sqrt {2}} ^ {{ sqrt {2}} ^ {1.63 }}}} & приблизительно { sqrt {2}} ^ {{ sqrt {2}} ^ {{ sqrt {2}} ^ {1.76}}} & приблизительно { sqrt {2 }} ^ {{ sqrt {2}} ^ {1.84}} & приблизительно { sqrt {2}} ^ {1.89} & приблизительно 1,93 end {выровнено}}}$

В общем случае бесконечно итерированная экспоненциальная ${ Displaystyle х ^ {х ^ { cdot ^ { cdot ^ { cdot}}}} ! !}$, определяемый как предел ${ Displaystyle {} ^ {п} х}$ так как п уходит в бесконечность, сходится за е^−е ≤ Икс ≤ е^1/е, примерно интервал от 0,066 до 1,44, результат показан как Леонард Эйлер.^[13] Предел, если он существует, является положительным действительным решением уравнения у = Икс^у. Таким образом, Икс = у^1/у. Предел, определяющий бесконечную тетрацию Икс не может сходиться для Икс > е^1/е потому что максимум у^1/у является е^1/е.

Это может быть расширено до комплексных чисел z с определением:

${ Displaystyle {} ^ { infty} z = z ^ {z ^ { cdot ^ { cdot ^ { cdot}}}} = { frac { mathrm {W} (- ln {z}) } {- ln {z}}} ~,}$

куда W представляет собой W-функция Ламберта.

Как предел у = ^∞Икс (если существует, т.е. для е^−е < Икс < е^1/е) должен удовлетворять Икс^у = у Мы видим, что Икс ↦ у = ^∞Икс является (нижняя ветвь) обратной функцией у ↦ Икс = у^1/у.

Отрицательные высоты

Мы можем использовать рекурсивное правило для тетрации,

${ displaystyle {^ {k + 1} a} = a ^ { left ({^ {k} a} right)},}$

чтобы доказать ${ displaystyle {} ^ {- 1} а}$:

${ displaystyle ^ {k} a = log _ {a} left (^ {k + 1} a right);}$

Подставляя −1 вместо k дает

${ displaystyle {} ^ {- 1} a = log _ {a} left ({} ^ {0} a right) = log _ {a} 1 = 0}$.^[10]

Таким образом нельзя точно определить меньшие отрицательные значения. Подставляя −2 вместо k в том же уравнении дает

${ displaystyle {} ^ {- 2} a = log _ {a} left ({} ^ {- 1} a right) = log _ {a} 0}$

который не совсем точно определен. Однако иногда их можно рассматривать как наборы.^[10]

За ${ Displaystyle п = 1}$, любое определение ${ Displaystyle , ! {^ {- 1} 1}}$ соответствует правилу, потому что

${ displaystyle {^ {0} 1} = 1 = 1 ^ {n}}$ для любого ${ Displaystyle , ! п = {^ {- 1} 1}}$.

Реальные высоты

Эта статья включает в себя список общих Рекомендации, но он остается в основном непроверенным, потому что ему не хватает соответствующих встроенные цитаты. Пожалуйста, помогите улучшать эта статья введение более точные цитаты. (Июль 2019) (Узнайте, как и когда удалить этот шаблон сообщения)

В настоящее время не существует общепринятого решения общей проблемы распространения тетрации на реальные или комплексные значения п. Однако к этому вопросу использовалось несколько подходов, и различные подходы изложены ниже.

В общем, проблема в поиске - для любого реального а > 0 - а суперэкспоненциальная функция ${ Displaystyle , е (х) = {} ^ {х} а}$ над реальным Икс > −2 это удовлетворяет

• ${ displaystyle , {} ^ {- 1} а = 0}$
• ${ Displaystyle , {} ^ {0} а = 1}$
• ${ displaystyle , {} ^ {x} a = a ^ { left ({} ^ {x-1} a right)}}$для всех реальных ${ displaystyle x> -1.}$^[14]

Чтобы найти более естественное расширение, обычно требуется одно или несколько дополнительных требований. Обычно это некоторая совокупность следующего:

• А непрерывность требование (обычно это ${ displaystyle {} ^ {x} а}$ непрерывна по обеим переменным при ${ displaystyle x> 0}$).
• А дифференцируемость требование (может быть один раз, два раза, k раз, или бесконечно дифференцируемые в Икс).
• А регулярность требование (подразумевающее дважды дифференцируемое по Икс) это:

${ displaystyle left ({ frac {d ^ {2}} {dx ^ {2}}} f (x)> 0 right)}$ для всех ${ displaystyle x> 0}$

Четвертое требование различается от автора к автору и от подходов. Есть два основных подхода к расширению тетрации до реальных высот; один основан на регулярность требование, и один основан на дифференцируемость требование. Эти два подхода кажутся настолько разными, что их невозможно согласовать, поскольку они дают результаты, несовместимые друг с другом.

Когда ${ displaystyle , {} ^ {x} а}$ определена для интервала длины один, вся функция легко следует для всех Икс > −2.

Линейное приближение для реальных высот

${ displaystyle , {} ^ {x} e}$ с использованием линейного приближения

А линейное приближение (решение требования непрерывности, приближение к требованию дифференцируемости) определяется как:

${ displaystyle {} ^ {x} a приблизительно { begin {cases} log _ {a} left (^ {x + 1} a right) & x leq -1 1 + x & -1 < x leq 0 a ^ { left (^ {x-1} a right)} & 0$

следовательно:

Значения линейной аппроксимации

Приближение	Домен
${ textstyle {} ^ {x} а приблизительно x + 1}$	за −1 < Икс < 0
${ textstyle {} ^ {x} а примерно а ^ {х}}$	за 0 < Икс < 1
${ textstyle {} ^ {x} а приблизительно а ^ {а ^ {(х-1)}}}$	за 1 < Икс < 2

и так далее. Однако она дифференцируема только кусочно; при целочисленных значениях Икс производная умножается на ${ Displaystyle ln {а}}$. Она непрерывно дифференцируема для ${ displaystyle x> -2}$ если и только если ${ displaystyle a = e}$. Например, используя эти методы ${ displaystyle {} ^ { frac { pi} {2}} e приблизительно 5,868 ...}$ и ${ displaystyle {} ^ {- 4.3} 0,5 приблизительно 4,03335 ...}$

Основная теорема в статье Хушманда^[7] заявляет: пусть ${ Displaystyle 0 <а neq 1}$. Если ${ displaystyle f: (- 2, + infty) rightarrow mathbb {R}}$ непрерывна и удовлетворяет условиям:

• ${ Displaystyle е (х) = а ^ {е (х-1)} ; ; { текст {для всех}} ; ; х> -1, ; f (0) = 1,}$
• ${ displaystyle f}$ дифференцируема на (−1, 0),
• ${ displaystyle f ^ { prime}}$ - неубывающая или невозрастающая функция на (−1, 0),
• ${ displaystyle f ^ { prime} left (0 ^ {+} right) = ( ln a) f ^ { prime} left (0 ^ {-} right) { text {или}} f ^ { prime} left (-1 ^ {+} right) = f ^ { prime} left (0 ^ {-} right).}$

тогда ${ displaystyle f}$ однозначно определяется уравнением

${ displaystyle f (x) = exp _ {a} ^ {[x]} left (a ^ {(x)} right) = exp _ {a} ^ {[x + 1]} (( x)) quad { text {для всех}} ; ; x> -2,}$

куда ${ Displaystyle (х) = х- [х]}$ обозначает дробную часть Икс и ${ Displaystyle ехр _ {а} ^ {[х]}}$ это ${ Displaystyle [х]}$-повторяющаяся функция функции ${ Displaystyle ехр _ {а}}$.

Доказательство состоит в том, что из условий со второго по четвертое тривиально следует, что ж является линейной функцией на [−1, 0].

Линейное приближение к естественной функции тетрации ${ displaystyle {} ^ {x} e}$ непрерывно дифференцируемо, но его вторая производная не существует при целых значениях аргумента. Хушманд вывел для него другую теорему единственности, которая гласит:

Если ${ displaystyle f: (- 2, + infty) rightarrow mathbb {R}}$ - непрерывная функция, удовлетворяющая:

• ${ Displaystyle е (х) = е ^ {е (х-1)} ; ; { текст {для всех}} ; ; х> -1, ; f (0) = 1,}$
• ${ displaystyle f}$ выпуклый на (−1, 0),
• ${ displaystyle f ^ { prime} left (0 ^ {-} right) leq f ^ { prime} left (0 ^ {+} right).}$

тогда ${ displaystyle f = { text {uxp}}}$. [Здесь ${ displaystyle f = { text {uxp}}}$ это имя Хушманда для линейного приближения к естественной функции тетрации.]

Доказательство почти такое же, как и раньше; рекурсивное уравнение гарантирует, что ${ displaystyle f ^ { prime} (- 1 ^ {+}) = f ^ { prime} (0 ^ {+}),}$ и тогда из условия выпуклости следует, что ${ displaystyle f}$ линейно на (−1, 0).

Следовательно, линейное приближение к естественной тетрации - единственное решение уравнения ${ Displaystyle е (х) = е ^ {е (х-1)} ; ; (х> -1)}$ и ${ displaystyle f (0) = 1}$ который выпуклый на (−1, +∞). Все остальные достаточно дифференцируемые решения должны иметь точка перегиба на интервале (−1, 0).

Аппроксимации высших порядков для реальных высот

Сравнение линейной и квадратичной аппроксимации (красным и синим цветом соответственно) функции ${ displaystyle ^ {x} 0,5}$, из Икс = −2 к Икс = 2

Помимо линейных приближений, a квадратичное приближение (к требованию дифференцируемости) определяется выражением:

${ displaystyle {} ^ {x} a приблизительно { begin {cases} log _ {a} left ({} ^ {x + 1} a right) & x leq -1 1 + { frac {2 ln (a)} {1 ; + ; ln (a)}} x - { frac {1 ; - ; ln (a)} {1 ; + ; ln (a)}} x ^ {2} & - 1 0 end {case}}}$

который дифференцируем для всех ${ displaystyle x> 0}$, но не дифференцируемые дважды. Например, ${ displaystyle {} ^ { frac {1} {2}} 2 приблизительно 1.45933 ...}$ Если ${ displaystyle a = e}$ это то же самое, что и линейное приближение.^[2]

Из-за способа вычисления эта функция не "сокращается", в отличие от экспонент, где ${ displaystyle left (a ^ { frac {1} {n}} right) ^ {n} = a}$. А именно,

${ displaystyle {} ^ {n} left ({} ^ { frac {1} {n}} a right) = underbrace { left ({} ^ { frac {1} {n}} a right) ^ { left ({} ^ { frac {1} {n}} a right) ^ { cdot ^ { cdot ^ { cdot ^ { cdot ^ { left ({} ^ { frac {1} {n}} a right)}}}}}} _ {n} neq a}$.

Так же, как есть квадратичное приближение, кубические приближения и методы обобщения до приближений степени п также существуют, хотя они гораздо более громоздкие.^[2][15]

Сложные высоты

Отрисовка аналитического расширения ${ Displaystyle е = F (х + { rm {i}} y)}$ тетрации на комплексную плоскость. Уровни ${ Displaystyle | е | = 1, е ^ { pm 1}, e ^ { pm 2}, ldots}$ и уровни ${ Displaystyle arg (е) = 0, pm 1, pm 2, ldots}$ показаны жирными кривыми.

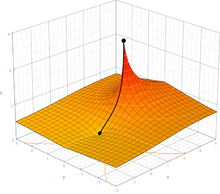
Теперь доказано^[16] что существует единственная функция F которое является решением уравнения F(z + 1) = ехр (F(z)) и удовлетворяет дополнительным условиям, что F(0) = 1 и F(z) приближается к фиксированные точки логарифма (примерно 0.318 ± 1.337я) в качестве z подходы ±я∞ и это F является голоморфный в целом комплексе z-плоскость, кроме части действительной оси на z ≤ −2. Это доказательство подтверждает предыдущее догадка.^[17] Построение такой функции было впервые продемонстрировано Кнезером в 1950 году.^[18] Сложная карта этой функции показана на рисунке справа. Доказательство работает и для других баз, кроме е, пока база больше, чем ${ displaystyle e ^ { frac {1} {e}} приблизительно 1,445}$. Последующие работы распространили строительство на все сложные базы. Комплексная аппроксимация этой функции с двойной точностью доступна в Интернете.^[19]

Требование голоморфности тетрации важно для ее уникальности. Многие функции S можно построить как

${ Displaystyle S (z) = F ! влево (~ z ~ + sum _ {n = 1} ^ { infty} sin (2 pi nz) ~ alpha _ {n} + sum _ {n = 1} ^ { infty} { Big (} 1- cos (2 pi nz) { Big)} ~ beta _ {n} right)}$

куда α и β реальные последовательности, которые распадаются достаточно быстро, чтобы обеспечить сходимость ряда, по крайней мере, при умеренных значениях Яz.

Функция S удовлетворяет уравнениям тетрации S(z + 1) = ехр (S(z)), S(0) = 1, и если α_п и β_п приближение к 0 достаточно быстро, оно будет аналитическим в окрестности положительной вещественной оси. Однако если некоторые элементы {α} или {β} не равны нулю, то функция S имеет множество дополнительных особенностей и разрезов в комплексной плоскости из-за экспоненциального роста sin и cos вдоль мнимой оси; чем меньше коэффициенты {α} и {β} являются, тем дальше эти особенности от действительной оси.

Распространение тетрации на комплексную плоскость, таким образом, существенно для уникальности; то аналитический тетрация не уникальна.

Неэлементарная рекурсивность

Тетрация (только ${ Displaystyle mathbb {N} ^ {2}}$) не элементарная рекурсивная функция. По индукции можно доказать, что для любой элементарной рекурсивной функции ж, есть постоянная c такой, что

${ displaystyle f (x) leq underbrace {2 ^ {2 ^ { cdot ^ { cdot ^ {x}}}}} _ {c}.}$

Обозначим правую часть через ${ Displaystyle г (с, х)}$. Предположим противное, что тетрация элементарно рекурсивна. ${ Displaystyle г (х, х) +1}$ также элементарно рекурсивно. По полученному неравенству существует постоянная c такой, что ${ Displaystyle г (х, х) +1 Leq г (с, х)}$. Позволяя ${ displaystyle x = c}$у нас есть это ${ Displaystyle г (с, с) +1 leq г (с, с)}$, противоречие.

Обратные операции

Возведение в степень имеет две обратные операции; корни и логарифмы. Аналогично обратное тетрации часто называют супер-корень, а суперлогарифм (Фактически, все гипероперации, большие или равные 3, имеют аналогичные обратные); например, в функции ${ Displaystyle {^ {3}} у = х}$, две обратные - кубический суперкорень у и основание суперлогарифмау из Икс.

Супер-корень

Суперкорень - это операция, обратная тетрации по отношению к основанию: если ${ Displaystyle ^ {п} у = х}$, тогда у является пй супер корень Икс (${ displaystyle { sqrt [{n}] {x}} _ {s}}$ или ${ displaystyle { sqrt [{n}] {x}} _ {4}}$).

Например,

${ displaystyle ^ {4} 2 = 2 ^ {2 ^ {2 ^ {2}}} = 65 {,} 536}$

Таким образом, 2 - это 4-й суперкорень из 65 536.

Квадратный суперкорень

График ${ displaystyle y = { sqrt {x}} _ {s}}$

В Суперкорень 2-го порядка, квадратный суперкорень, или же супер квадратный корень имеет два эквивалентных обозначения, ${ Displaystyle mathrm {ssrt} (х)}$ и ${ displaystyle { sqrt {x}} _ {s}}$. Это обратное ${ Displaystyle ^ {2} х = х ^ {х}}$ и может быть представлен W функция Ламберта:^[20]

${ Displaystyle mathrm {ssrt} (х) = е ^ {W ( ln x)} = { frac { ln x} {W ( ln x)}}}$

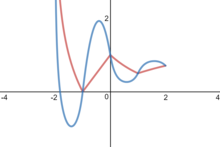
Функция также иллюстрирует отражающую природу функций корня и логарифма, поскольку приведенное ниже уравнение справедливо только тогда, когда ${ Displaystyle у = mathrm {ssrt} (х)}$:

${ displaystyle { sqrt [{y}] {x}} = log _ {y} x}$

подобно квадратные корни, квадратный суперкорень из Икс может не иметь единого решения. В отличие от квадратных корней, определение количества квадратных суперкорней Икс может быть сложно. В общем, если ${ Displaystyle е ^ {- 1 / е} <х <1}$, тогда Икс имеет два положительных квадратных суперкорня от 0 до 1; и если ${ displaystyle x> 1}$, тогда Икс имеет один положительный квадратный суперкорень больше 1. Если Икс положительно и меньше ${ displaystyle e ^ {- 1 / e}}$ у него нет никаких настоящий квадратные суперкорни, но приведенная выше формула дает счетное бесконечное число сложный единицы для любых конечных Икс не равно 1.^[20] Функция была использована для определения размера кластеры данных.^[21]

В ${ displaystyle x = 1}$:

${ displaystyle mathrm {ssqrt} (x) = 1 + (x-1) - (x-1) ^ {2} + { frac {3} {2}} (x-1) ^ {3} - { frac {17} {6}} (x-1) ^ {4} + { frac {37} {6}} (x-1) ^ {5} - { frac {1759} {120}} (x-1) ^ {6} + { frac {13279} {360}} (x-1) ^ {7} + mathrm {O} left ((x-1) ^ {8} right) }$

Другие супер-корни

График ${ displaystyle y = { sqrt [{3}] {x}} _ {s}}$

Для каждого целого числа п > 2, функция ^пИкс определяется и увеличивается для Икс ≥ 1, и ^п1 = 1, таким образом пй суперкорень Икс, ${ displaystyle { sqrt [{n}] {x}} _ {s}}$существует для Икс ≥ 1.

Одной из более простых и быстрых формул суперкорня третьей степени является рекурсивная формула, если: «x ^ x ^ x = a», а затем x (n + 1) = exp (W (W (x (n ) * ln (a)))), например x (0) = 1.

Однако если линейное приближение выше используется, то ${ Displaystyle ^ {у} х = у + 1}$ если −1 < у ≤ 0, так ${ displaystyle ^ {y} { sqrt {y + 1}} _ {s}}$ не может существовать.

Так же, как и квадратный суперкорень, терминология для других суперкорней может быть основана на нормальные корни: "кубические суперкорни" можно выразить как ${ displaystyle { sqrt [{3}] {x}} _ {s}}$; «4-й суперкорень» можно выразить как ${ displaystyle { sqrt [{4}] {x}} _ {s}}$; и "пй супер-корень " ${ displaystyle { sqrt [{n}] {x}} _ {s}}$. Обратите внимание, что ${ displaystyle { sqrt [{n}] {x}} _ {s}}$ не может быть однозначно определено, потому что может быть более одного п^th корень. Например, Икс имеет единственный (настоящий) суперкорень, если п является странный, и до двух, если п является даже.^{[нужна цитата]}

Так же, как с расширением тетрации до бесконечных высот, суперкорень может быть расширен до п = ∞, будучи хорошо определенным, если 1/е ≤ Икс ≤ е. Обратите внимание, что ${ displaystyle x = {^ { infty} y} = y ^ { left [^ { infty} y right]} = y ^ {x},}$ и таким образом ${ Displaystyle у = х ^ {1 / х}}$. Следовательно, когда он четко определен, ${ displaystyle { sqrt [{ infty}] {x}} _ {s} = x ^ {1 / x}}$ и, в отличие от обычной тетрации, является элементарная функция. Например, ${ displaystyle { sqrt [{ infty}] {2}} _ {s} = 2 ^ {1/2} = { sqrt {2}}}$.

Это следует из Теорема Гельфонда – Шнайдера этот супер-корень ${ displaystyle { sqrt {n}} _ {s}}$ для любого положительного целого числа п либо целое, либо трансцендентный, и ${ displaystyle { sqrt [{3}] {n}} _ {s}}$ либо целое, либо иррациональное.^[22] Остается открытым вопрос, являются ли иррациональные суперкорни трансцендентными в последнем случае.

Суперлогарифм

После непрерывного увеличения (в Икс) определение тетрации, ^Икса, выбран соответствующий суперлогарифм ${ displaystyle operatorname {slog} _ {a} x}$ или ${ Displaystyle журнал _ {а} ^ {4} х}$ определено для всех действительных чисел Икс, и а > 1.

Функция тяжелая работа_а Икс удовлетворяет:

${ displaystyle { begin {array} {lcl} operatorname {slog} _ {a} {^ {x} a} & = & x operatorname {slog} _ {a} a ^ {x} & = & 1+ operatorname {slog} _ {a} x operatorname {slog} _ {a} x & = & 1+ operatorname {slog} _ {a} log _ {a} x operatorname {slog} _ {a } x &> & - 2 end {массив}}}$

Открытые вопросы

Помимо проблем с расширениями тетрации, есть несколько открытых вопросов, касающихся тетрации, особенно когда речь идет об отношениях между системами счисления, такими как целые числа и иррациональные числа:

• Неизвестно, существует ли положительное целое число п для которого ^пπ или ^пе целое число. В частности, неизвестно, были ли ⁴π или ⁵е целое число.^{[нужна цитата]}
• Неизвестно, были ли ^пq является целым числом для любого положительного целого числа п и положительные нецелые рациональные q.^[22] В частности, неизвестно, является ли положительный корень уравнения ⁴Икс = 2 - рациональное число.^{[нужна цитата]}

Смотрите также

Викискладе есть медиафайлы по теме тетрация.

• Функция Аккермана
• Обозначение Big O
• Двойная экспоненциальная функция
• Гипероперация
• Итерированный логарифм
• Симметричная арифметика индекса уровня

Примечания

Рекомендации

• Даниэль Гейслер, Тетрация
• Иоаннис Галидакис, О расширении hyper4 до нецелых чисел (без даты, 2006 г. или ранее) (Более простой и понятный обзор следующей ссылки)
• Иоаннис Галидакис, О распространении нотации Hyper4 и стрелки вверх Кнута на вещественные числа (без даты, 2006 г. или ранее).
• Роберт Мунафо, Расширение функции hyper4 на реалы (Неформальная дискуссия о расширении тетрации до действительных чисел.)
• Лоде Вандевенн, Тетрация квадратного корня из двух. (2004). (Попытка распространить тетрацию на действительные числа.)
• Иоаннис Галидакис, Математика, (Окончательный список ссылок на исследования тетрации. Много информации о W-функции Ламберта, римановых поверхностях и аналитическом продолжении.)
• Джозеф МакДонелл, Некоторые критические моменты функции гиперсилы.
• Дэйв Л. Ренфро, Веб-страницы для бесконечно повторяющихся экспонент
• Кнобель, Р. (1981). «Экспоненты повторяются». Американский математический ежемесячный журнал. 88 (4): 235–252. Дои:10.1080/00029890.1981.11995239.
• Ханс Маурер, "Über die Funktion" ${ Displaystyle у = х ^ {[х ^ {[х ( cdots)]}]}}$ für ganzzahliges Argument (Abundanzen) ". Mittheilungen der Mathematische Gesellschaft в Гамбурге 4, (1901), стр. 33–50. (Ссылка на использование ${ Displaystyle {^ {п} а}}$ из статьи Кнобеля.)
• Четвертая операция
• Лука Морони, Странные свойства башни бесконечной силы (https://arxiv.org/abs/1908.05559)

дальнейшее чтение

• Галидакис, Иоаннис; Вайсштейн, Эрик Вольфганг. «Энергетическая башня». MathWorld. Получено 2019-07-05.