WikiDer > Распределение квазивероятностей Вигнера

В Распределение квазивероятностей Вигнера (также называемый Функция Вигнера или Распределение Вигнера – Вилля после Юджин Вигнер и Жан-Андре Вилль) это распределение квазивероятностей. Было введено[1] Юджином Вигнером в 1932 году для изучения квант поправки к классическим статистическая механика. Целью было связать волновая функция что появляется в Уравнение Шредингера к распределению вероятностей в фазовое пространство.
Это производящая функция для всех пространственных автокорреляция функции данной квантово-механической волновой функции ψ(Икс)Таким образом, он отображает[2] на квантовом матрица плотности в карте между реальными функциями фазового пространства и Эрмитский операторы введены Герман Вейль в 1927 г.,[3] в контексте, связанном с теория представлений по математике (ср. Квантование Вейля по физике). По сути, это Преобразование Вигнера – Вейля матрицы плотности, поэтому реализация этого оператора в фазовом пространстве. Позже он был переработан Жаном Виллем в 1948 году как квадратичный (по сигналу) представление локальной частотно-временной энергии сигнала,[4] эффективно спектрограмма.
В 1949 г. Хосе Энрике Мойаль, который вывел его независимо, признал его квант моментобразующий функционал,[5] и, таким образом, как основа элегантного кодирования всех значений квантового ожидания и, следовательно, квантовой механики в фазовом пространстве (см. формулировка фазового пространства). Он имеет приложения в статистическая механика, квантовая химия, квантовая оптика, классический оптика и анализ сигналов в различных областях, таких как электротехника, сейсмология, частотно-временной анализ музыкальных сигналов, спектрограммы в биология и обработка речи, и конструкция двигателя.
Отношение к классической механике
Классическая частица имеет определенное положение и импульс и, следовательно, представлена точкой в фазовом пространстве. Учитывая коллекцию (ансамбль) частиц вероятность нахождения частицы в определенной позиции в фазовом пространстве определяется распределением вероятностей, плотностью Лиувилля. Эта строгая интерпретация не подходит для квантовой частицы из-за принцип неопределенности. Вместо этого указанное выше распределение Вигнера квазивероятностей играет аналогичную роль, но не удовлетворяет всем свойствам обычного распределения вероятностей; и, наоборот, удовлетворяет свойствам ограниченности, недоступным для классических распределений.
Например, распределение Вигнера может принимать и обычно принимает отрицательные значения для состояний, не имеющих классической модели, и является удобным индикатором квантово-механической интерференции. (См. Ниже характеристику чистых состояний, функции Вигнера которых неотрицательны.) Сглаживание распределения Вигнера с помощью фильтра размером больше час (например, свертка с гауссовым фазовым пространством, Преобразование Вейерштрасса, чтобы получить Представительство Хусиминиже), приводит к положительно-полуопределенной функции, т. е. можно подумать, что она была огрублена до полуклассической.[а]
Области с таким отрицательным значением можно доказать (сворачивая их с помощью небольшого гаусса) как «маленькие»: они не могут распространяться на компактные области размером больше нескольких час, а значит, исчезнут в классический предел. Они защищены принцип неопределенности, что не позволяет точно расположить в областях фазового пространства меньше, чем час, и таким образом делает такой "отрицательные вероятности"менее парадоксально.
Определение и значение
Распределение Вигнера W(Икс,п) чистого состояния определяется как:
куда ψ - волновая функция и Икс и п являются положением и импульсом, но могут быть любой парой сопряженных переменных (например, действительная и мнимая части электрического поля или частота и время сигнала). Обратите внимание, что он может иметь поддержку в Икс даже в регионах, где ψ не имеет поддержки в Икс («бьет»).
Он симметричен по Икс и п,
куда φ - нормированная волновая функция в импульсном пространстве, пропорциональная преобразование Фурье из ψ.
В 3D,
В общем случае, включающем смешанные состояния, это преобразование Вигнера матрица плотности,
куда ⟨Икс|ψ⟩ = ψ (х). Этот Преобразование Вигнера (или карта) - это обратное Преобразование Вейля, который отображает функции фазового пространства в Гильбертово пространство операторов, в Квантование Вейля.
Таким образом, функция Вигнера является краеугольным камнем квантовая механика в фазовое пространство.
В 1949 г. Хосе Энрике Мойаль объяснил, как функция Вигнера обеспечивает меру интегрирования (аналогично функция плотности вероятности) в фазовом пространстве, чтобы получить ожидаемые значения из фазового пространства c-число функции грамм(Икс,п) однозначно ассоциируется с правильно упорядоченными операторами ГРАММ через преобразование Вейля (ср. Преобразование Вигнера – Вейля и свойство 7 ниже) в манере классической теория вероятности.
В частности, операторский ГРАММ математическое ожидание представляет собой "среднее фазовое пространство" преобразования Вигнера этого оператора,
Математические свойства

1. W(Икс, п) - вещественная функция.
2. Программа Икс и п распределения вероятностей даются маргиналы:
- Если систему можно описать чистое состояние, получается .
- Если систему можно описать чистое состояние, надо .
- Обычно след матрицы плотности ρ̂ равно 1.
3. W(Икс, п) имеет следующие симметрии отражения:
- Симметрия времени:
- Симметрия пространства:
4. W(Икс, п) ковариантно по Галилею:
- Это не так Ковариант Лоренца.
5. Уравнение движения для каждой точки фазового пространства является классическим при отсутствии сил:
- Фактически, это классический стиль даже при наличии гармонических сил.
6. Перекрытие состояний рассчитывается как:
7. Ожидаемые операторы (средние) вычисляются как средние по фазовому пространству соответствующих преобразований Вигнера:
8. Для того, чтобы W(Икс, п) представляют собой физические (положительные) матрицы плотности:
- для всех чистых состояний | θ〉.
9. В силу Неравенство Коши – Шварца, для чистого состояния оно ограничено,
- Эта оценка исчезает в классическом пределе, час → 0. В этом пределе W(Икс, п) сводится к плотности вероятности в координатном пространстве Икс, обычно сильно локализованные, умноженные на δ-функции по импульсу: классический предел - "остроконечный". Таким образом, эта квантово-механическая граница исключает функцию Вигнера, которая является идеально локализованной дельта-функцией в фазовом пространстве, как отражение принципа неопределенности.[6]
10. Преобразование Вигнера - это просто преобразование Фурье из антидиагонали матрицы плотности, когда эта матрица выражена в позиционном базисе.[7]
Примеры
Позволять быть -го Состояние Фока из квантовый гармонический осциллятор. Groenewold (1946) обнаружил, что ассоциированная с ней функция Вигнера в безразмерных переменных есть
Это может вытекать из выражения для статических волновых функций собственного состояния: ,куда это -го Многочлен Эрмита. Из приведенного выше определения функции Вигнера после замены переменных интегрирования
Тогда выражение следует из интегрального соотношения между многочленами Эрмита и Лагерра.[8]
Уравнение эволюции для функции Вигнера
В Преобразование Вигнера - общее обратимое преобразование оператора ГРАММ на Гильбертово пространство к функции г (х, р) на фазовое пространство, и задается
Эрмитовы операторы отображаются в вещественные функции. Обратное к этому преобразованию, то есть из фазового пространства в гильбертово пространство, называется Преобразование Вейля,
(не путать с отличным Преобразование Вейля в дифференциальной геометрии).
В Функция Вигнера W(х, р), обсуждаемое здесь, рассматривается как преобразование Вигнера матрица плотности оператор ρ̂. Таким образом, след оператора с матрицей плотности Вигнера превращается в эквивалентное перекрытие интеграла фазового пространства грамм(Икс, п) с функцией Вигнера.
Преобразование Вигнера уравнение эволюции фон Неймана матрицы плотности в Картина Шредингера является
- Уравнение эволюции Мойала для функции Вигнера,
где H (x, p) - гамильтониан, а {{•, •}} - Кронштейн Мойял. В классическом пределе час → 0 скобка Мойала сводится к скобке Пуассона, а это уравнение эволюции сводится к Уравнение Лиувилля классической статистической механики.
Строго формально, с точки зрения квантовые характеристики, решение этого эволюционного уравнения имеет вид ,куда и являются решениями так называемых квантовые уравнения Гамильтона, при начальных условиях и , и где -товаркомпозиция понимается для всех функций аргумента.
Однако поскольку -композиция полностью нелокальна («квантовая вероятностная жидкость» распространяется, как наблюдал Мойал), остатки локальных траекторий обычно едва различимы в эволюции функции распределения Вигнера.[b]В интегральном представлении ★-продукты, последовательные операции с ними были адаптированы к интегралу по путям в фазовом пространстве, чтобы решить это уравнение эволюции для функции Вигнера [9] (смотрите также [10][11][12]Эта нетраекторная особенность временной эволюции Мойала.[13] показано в галерее ниже для гамильтонианов, более сложных, чем гармонический осциллятор.
- Примеры временной эволюции функции Вигнера
Чистое состояние в Потенциал Морзе. Зеленые пунктирные линии представляют набор уровней из Гамильтониан.
Чистое состояние в потенциале четвертой степени. Сплошные линии представляют набор уровней из Гамильтониан.
Туннелирование из волновой пакет через потенциальный барьер. Сплошные линии представляют набор уровней из Гамильтониан.
Длительная эволюция смешанного состояния ρ в ангармонической потенциальной яме. Маржа отображается справа (п) и верхний (Икс).
Временная эволюция гармонического осциллятора
В частном случае квантовый гармонический осцилляторОднако эволюция проста и выглядит идентичной классическому движению: жесткое вращение в фазовом пространстве с частотой, заданной частотой осциллятора. Это показано в галерее ниже. В то же время эволюция происходит с квантовые состояния световых мод, которые являются гармоническими осцилляторами.
- Примеры временной эволюции функции Вигнера в квантовом гармоническом осцилляторе
Комбинированное основное состояние и 1-е возбужденное состояние.[14]
А состояние кошки; то маргиналы нанесены справа (п) и под (Икс).
Классический предел
Функция Вигнера позволяет изучать классический предел, предлагая сравнение классической и квантовой динамики в фазовом пространстве.[15][16]
Недавно было высказано предположение, что подход с использованием функций Вигнера можно рассматривать как квантовую аналогию операторной формулировке классической механики, введенной в 1932 г. Бернард Купман и Джон фон Нейман: временная эволюция функции Вигнера приближается в пределе час → 0, временная эволюция Волновая функция Купмана – фон Неймана классической частицы.[17]
В усеченное приближение Вигнера является квазиклассическим приближением динамики, полученной заменой уравнения Мойала на классическое Уравнение Лиувилля.[нужна цитата]
Положительность функции Вигнера.
Как уже отмечалось, функция квантового состояния Вигнера обычно принимает некоторые отрицательные значения. Действительно, для чистого состояния с одной переменной, если для всех и , то волновая функция должна иметь вид
для некоторых комплексных чисел с (Теорема Хадсона[18]). Обратите внимание, что может быть сложным, так что не обязательно является гауссовским волновым пакетом в обычном смысле. Таким образом, чистые состояния с неотрицательными функциями Вигнера не обязательно являются состояниями минимальной неопределенности в смысле Формула неопределенности Гейзенберга; скорее, они дают равенство в Формула неопределенности Шредингера, который включает в себя член антикоммутатора в дополнение к члену коммутатора. (При тщательном определении соответствующих дисперсий все функции Вигнера в чистом состоянии все равно приводят к неравенству Гейзенберга.)
В более высоких измерениях характеристика чистых состояний с неотрицательными функциями Вигнера аналогична; волновая функция должна иметь вид
куда - симметричная комплексная матрица, вещественная часть которой положительно определена, - комплексный вектор, а c - комплексное число.[19] Функция Вигнера любого такого состояния - это гауссово распределение на фазовом пространстве.
В цитируемой статье Сото и Клавери дается элегантное доказательство этой характеристики с использованием Преобразование Сегала – Баргмана. Аргументация следующая. В Функция Хусими Q из может быть вычислен как квадрат величины преобразования Сигала – Баргмана , умноженное на гауссиан. Между тем, функция Хусими Q представляет собой свертку функции Вигнера с гауссовой. Если функция Вигнера неотрицательна всюду на фазовом пространстве, то функция Хусими Q будет строго положительной всюду на фазовом пространстве. Таким образом, преобразование Сегала – Баргмана из нигде не будет ноль. Таким образом, по стандартному результату комплексного анализа имеем
для некоторой голоморфной функции . Но для того, чтобы принадлежать к Пространство Сегала – Баргмана.- то есть для быть интегрируемым с квадратом относительно гауссовской меры - должен иметь не более чем квадратичный рост на бесконечности. Отсюда элементарный комплексный анализ может быть использован, чтобы показать, что фактически должен быть квадратичным многочленом. Таким образом, мы получаем явный вид преобразования Сигала – Баргмана для любого чистого состояния, функция Вигнера которого неотрицательна. Затем мы можем инвертировать преобразование Сегала – Баргмана, чтобы получить заявленную форму волновой функции положения.
Кажется, нет простой характеристики смешанные государства с неотрицательными функциями Вигнера.
Функция Вигнера по отношению к другим интерпретациям квантовой механики
Было показано, что функцию распределения квазивероятностей Вигнера можно рассматривать как час-деформация другой функции распределения фазового пространства, описывающей ансамбль де Бройль-Бом причинные траектории.[20] Бэзил Хили показал, что квазивероятностное распределение можно понимать как матрица плотности перевыражается через среднее положение и импульс «ячейки» в фазовом пространстве, и интерпретация де Бройля – Бома позволяет описать динамику центров таких «ячеек».[21][22]
Существует тесная связь между описанием квантовых состояний в терминах функции Вигнера и методом реконструкции квантовых состояний в терминах взаимно объективные основы.[23]
Использование функции Вигнера вне квантовой механики

- При моделировании оптических систем, таких как телескопы или оптоволоконные телекоммуникационные устройства, функция Вигнера используется для преодоления разрыва между простыми трассировка лучей и полный волновой анализ системы. Здесь p / ħ заменяется на k = |k| грехθ ≈ |k|θ в малоугловом (параксиальном) приближении. В этом контексте функция Вигнера является наиболее близкой к описанию системы в терминах лучей в положении Икс и угол θ при этом еще с учетом эффектов помех.[24] Если в какой-то момент он станет отрицательным, то простой трассировки лучей будет недостаточно для моделирования системы. То есть отрицательные значения этой функции являются признаком неисправности. Предел Габора классического светового сигнала и нет квантовых характеристик света, связанных с час.
- В анализ сигналов, изменяющийся во времени электрический сигнал, механическая вибрация или звуковая волна представлены Функция Вигнера. Здесь, Икс заменяется временем и p / ħ заменяется на угловую частоту ω = 2πж, куда ж - обычная частота.
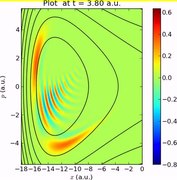
- В сверхбыстрой оптике короткие лазерные импульсы характеризуются функцией Вигнера с использованием того же ж и т замены, как указано выше. Дефекты импульса, такие как щебетание (изменение частоты со временем), могут быть визуализированы с помощью функции Вигнера. См. Рисунок рядом.
- В квантовой оптике Икс и p / ħ заменены на Икс и п квадратуры, действительные и мнимые компоненты электрического поля (см. когерентное состояние).
Измерения функции Вигнера.
Распределение Вигнера было первым квазивероятным распределением, которое было сформулировано, но за ним последовали многие другие, формально эквивалентные и трансформируемые в него и из него (т. Е. Преобразование между распределениями в частотно-временном анализе). Как и в случае систем координат, из-за различных свойств некоторые из них имеют различные преимущества для конкретных приложений:
Тем не менее, в некотором смысле распределение Вигнера занимает привилегированное положение среди всех этих распределений, поскольку оно только один чей необходимый звездный продукт выпадает (интегрируется по частям до эффективной единицы) при оценке ожидаемых значений, как показано выше, и поэтому может визуализироваться как мера квазивероятностей, аналогичная классическим.
Историческая справка
Как указано, формула для функции Вигнера независимо выводилась несколько раз в разных контекстах. На самом деле, видимо, Вигнер не знал, что даже в контексте квантовой теории она была введена ранее Гейзенберг и Дирак,[25] хотя и чисто формально: эти двое упустили его значение и значение его отрицательных значений, поскольку они просто рассматривали его как приближение к полному квантовому описанию такой системы, как атом. (Между прочим, Дирак позже стал зятем Вигнера, женившись на его сестре Manci.) Симметрично, в большей части его легендарной 18-месячной переписки с Мойал В середине 1940-х годов Дирак не знал, что производящая функция Мойала по сути является функцией Вигнера, и именно Мойал наконец привлек его внимание.[26]
Смотрите также
Сноски
- ^ В частности, поскольку эта свертка обратима, фактически никакая информация не была принесена в жертву, и полная квантовая энтропия еще не увеличилась. Однако, если это результирующее распределение Хусими затем используется как простая мера в интегральной оценке фазового пространства ожидаемых значений без необходимого звездного продукта представления Хусими, то на этом этапе квантовая информация был конфискован и распределение полуклассический, эффективно. То есть, в зависимости от его использования при оценке ожидаемых значений, само одно и то же распределение может служить квантовой или классической функцией распределения.
- ^ Квантовые характеристики не следует путать с траекториями интеграла по путям Фейнмана или траекториямитеория де Бройля - БомаЭта тройная двусмысленность позволяет лучше понять положение Нильс Бор, который энергично, но контрпродуктивно выступал против концепции траектории в атомной физике. Например, на конференции в Поконо в 1948 году он сказал: Ричард Фейнман: «… Нельзя было говорить о траектории электрона в атоме, потому что это было чем-то ненаблюдаемым». («Удар другого барабана: жизнь и наука Ричарда Фейнмана», автор Джагдиш Мехра (Оксфорд, 1994) , pp. 245-248)). Аргументы такого рода широко использовались в прошлом Эрнст Мах в своей критике атомной теории физики, а затем, в 1960-х годах, Джеффри Чу, Туллио Редже и другие, чтобы мотивировать замену локальной квантовой теории поля на S-матрица Сегодня статистическая физика, полностью основанная на атомистических концепциях, входит в стандартные курсы, теория S-матриц вышла из моды, а метод интегралов по путям Фейнмана признан наиболее эффективным методом в калибровочные теории.
Рекомендации
- ^ Э. П. Вигнер (1932). «О квантовой поправке за термодинамическое равновесие». Phys. Rev. 40 (5): 749–759. Bibcode:1932PhRv ... 40..749Вт. Дои:10.1103 / PhysRev.40.749. HDL:10338.dmlcz / 141466.
- ^ Х. Дж. Греневольд (1946). «О принципах элементарной квантовой механики». Physica. 12 (7): 405–460. Bibcode:1946Phy .... 12..405G. Дои:10.1016 / S0031-8914 (46) 80059-4.
- ^ Х. Вейль (1927). "Quantenmechanik und gruppentheorie". Z. Phys. 46 (1–2): 1. Bibcode:1927ZPhy ... 46 .... 1Вт. Дои:10.1007 / BF02055756. S2CID 121036548.; Х. Вейль, Gruppentheorie und Quantenmechanik (Лейпциг: Hirzel) (1928); Х. Вейль, Теория групп и квантовая механика (Довер, Нью-Йорк, 1931).
- ^ Ж. Вилль, "Теория и приложения аналитического понятия", Кабели и трансмиссия, 2, 61–74 (1948).
- ^ Дж. Э. Мойал, «Квантовая механика как статистическая теория», Труды Кембриджского философского общества, 45, 99–124 (1949). Дои:10.1017 / S0305004100000487
- ^ Curtright, T. L .; Захос, К. К. (2012). «Квантовая механика в фазовом пространстве». Информационный бюллетень по физике Азиатско-Тихоокеанского региона. 01: 37. arXiv:1104.5269. Дои:10.1142 / S2251158X12000069. S2CID 119230734.; К. Захос, Д. Фэрли и Т. Кертрайт, Квантовая механика в фазовом пространстве (World Scientific, Сингапур, 2005 г.) ISBN 978-981-238-384-6.
- ^ Хоукс, Питер У. (2018). Достижения в области визуализации и электронной физики. Академическая пресса. п. 47. ISBN 9780128155424.
- ^ Шлейх, Вольфганг П. (2001-02-09). Квантовая оптика в фазовом пространстве (1-е изд.). Вайли. Дои:10.1002/3527602976. ISBN 978-3-527-29435-0. стр.105
- ^ Б. Лиф (1968). «Преобразование Вейля в нерелятивистской квантовой динамике». J. Math. Phys. 9 (5): 769–781. Bibcode:1968JMP ..... 9..769L. Дои:10.1063/1.1664640.
- ^ П. Шаран (1979). "Звездное произведение интегралов по путям". Phys. Ред. D. 20 (2): 414–418. Bibcode:1979ПхРвД..20..414С. Дои:10.1103 / PhysRevD.20.414.
- ^ М. С. Маринов (1991). «Новый тип интеграла по траекториям в фазовом пространстве». Phys. Lett. А. 153 (1): 5–11. Bibcode:1991ФЛА..153 .... 5М. Дои:10.1016/0375-9601(91)90352-9.
- ^ Б. Сегев: Ядра эволюции для распределений в фазовом пространстве. В: Ольшанецкий М.А. (ред.); Аркадий Вайнштейн (ред.) (2002). Множественные аспекты квантования и суперсимметрии: мемориальный том Михаила Маринова. World Scientific. С. 68–90. ISBN 978-981-238-072-2. Получено 26 октября 2012.CS1 maint: дополнительный текст: список авторов (связь) особенно см. раздел 5. «Интеграл по траекториям для пропагатора» на страницы 86-89онлайн
- ^ М. Олива, Д. Какофенгитис и О. Штойернагель (2018). «Ангармонические квантово-механические системы не имеют траекторий фазового пространства». Physica A. 502: 201–210. arXiv:1611.03303. Bibcode:2018PhyA..502..201O. Дои:10.1016 / j.physa.2017.10.047. S2CID 53691877.CS1 maint: несколько имен: список авторов (связь)
- ^ а б Кертрайт, Т.Л., Зависящие от времени функции Вигнера
- ^ См. Например: Войцех Х. Зурек: Декогеренция и переход от квантовой к классической - повторный визит, Los Alamos Science, 27, 2002, arXiv: Quant-ph / 0306072, стр. 15 и сл.
- ^ См., Например: C. Zachos, D. Fairlie, T. Curtright: Квантовая механика в фазовом пространстве: обзор избранных статей, World Scientific, 2005 ISBN 978-981-4520-43-0
- ^ Бондарь, Денис И .; Кабрера, Ренан; Жданов, Дмитрий В .; Рабиц, Гершель А. (2013). «Вигнеровское фазовое распределение как волновая функция». Физический обзор A. 88 (5): 052108. arXiv:1202.3628. Дои:10.1103 / PhysRevA.88.052108. ISSN 1050-2947. S2CID 119155284.
- ^ Хадсон, Робин Л. (1974). «Когда плотность квази-вероятностей Вигнера неотрицательна?». Доклады по математической физике. 6 (2): 249–252. Bibcode:1974RpMP .... 6..249H. Дои:10.1016 / 0034-4877 (74) 90007-X.
- ^ Ф. Сото и П. Клавери, "Когда функция Вигнера многомерных систем неотрицательна?", Журнал математической физики 24 (1983) 97-100
- ^ Нуно Коста Диас, Жоао Нуно Прата, Бомовские траектории и распределения квантового фазового пространства, Physics Letters A vol. 302 (2002) стр. 261-272, Дои:10.1016 / S0375-9601 (02) 01175-1 arXiv: Quant-ph / 0208156v1 (подано 26 августа 2002 г.)
- ^ Б. Дж. Хили: Описание квантовых явлений в фазовом пространстве, в: А. Хренников (ред.): Квантовая теория: переосмысление основ – 2, стр. 267-286, Växjö University Press, Швеция, 2003 (PDF)
- ^ Б. Хили: Характеристическая функция Мойала, матрица плотности и идемпотент фон Неймана (препринт)
- ^ F.C. Ханна, П.А. Мелло, М. Ревзен, Классическая и квантово-механическая реконструкция состояния, arXiv: 1112.3164v1 [Quant-ph] (представлена 14 декабря 2011 г.)
- ^ Я Базаров, Phys Rev ST Ускоряющие пучки 15 (2012) 050703, Дои:10.1103 / PhysRevSTAB.15.050703.
- ^ В. Гейзенберг, "Über die inkohärente Streuung von Röntgenstrahlen", Physik. Zeitschr. 32, 737–740 (1931); P.A.M. Дирак, «Замечание об обменных явлениях в атоме Томаса», Proc. Camb. Фил. Soc. 26, 376–395 (1930). Дои:10.1017 / S0305004100016108
- ^ Энн Мойал, (2006), «Математик Maverick: жизнь и наука Дж. Э. Мойала», ANU E-press, 2006, ISBN 1-920942-59-9, доступ к http://epress.anu.edu.au/maverick_citation.html
дальнейшее чтение
- М. Леванда, В. Флёров, "Функция квазираспределения Вигнера для заряженных частиц в классических электромагнитных полях", Анналы физики, 292, 199–231 (2001). arXiv:cond-mat / 0105137
внешняя ссылка
- Вигнер Реализация функции Вигнера в QuTiP.
- Галерея квантовой оптики
- Сонограмма видимой речи Под лицензией GPL распространяется бесплатное программное обеспечение для квазивероятностного распределения файлов сигналов Вигнера.