WikiDer > Базовый номер репродукции
| Болезнь | Передача инфекции | |
|---|---|---|
| Корь | Аэрозоль | 12–18[2] |
| Ветряная оспа (ветряная оспа) | Аэрозоль | 10–12[3] |
| Свинка | Респираторные капли | 10–12[4] |
| Полиомиелит | Фекально-оральный путь | 5–7[5] |
| Краснуха | Респираторные капли | 5–7[6] |
| Коклюш | Респираторные капли | 5.5[7] |
| Оспа | Респираторные капли | 3.5–6[8] |
| ВИЧ / СПИД | Телесные жидкости | 2–5[нужна цитата] |
| ОРВИ | Респираторные капли | 0.19–1.08[9] |
| COVID-19 | Респираторные капли и аэрозоль[10] | 2–6 (без социального дистанцирования)[11][12] |
| Простуда | Респираторные капли | 2–3[13] |
| Дифтерия | Слюна | 1.7–4.3[14] |
| Грипп (Пандемия 1918 года напряжение) | Респираторные капли | 1.4–2.8[15] |
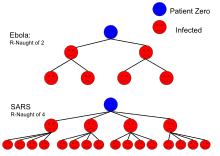
| Эбола (Вспышка Эболы в 2014 г.) | Телесные жидкости | 1.5–1.9[16] |
| Грипп (Пандемия 2009 г. напряжение) | Респираторные капли | 1.4–1.6[17] |
| Грипп (сезонные сорта) | Респираторные капли | 0.9–2.1[18] |
| MERS | Респираторные капли | 0.3–0.8[19] |
| Вирус нипах | Телесные жидкости | 0.48[20] |
В эпидемиология, то базовый номер репродукции, или же базовое репродуктивное число (иногда называют базовый коэффициент воспроизведения или же базовая скорость воспроизводства), обозначенный (произносится R нет или же R ноль),[21] из инфекционное заболевание можно рассматривать как ожидаемое число случаев, непосредственно порожденных одним случаем в популяции, где все люди восприимчивый к инфекции.[17] Определение описывает состояние, в котором другие люди не инфицированы или иммунизированный (естественно или через вакцинация). Некоторые определения, например, Департамент здравоохранения Австралиидобавить отсутствие «какого-либо преднамеренного вмешательства в передачу болезни».[22] Не следует путать базовый номер репродукции с эффективное репродуктивное число (обычно пишется [т на время], иногда ),[23] что является количеством случаев, генерируемых в текущем состоянии популяции, которое не обязательно должно быть незараженным. Также важно отметить, что безразмерное число, а не скорость, которая будет иметь единицы времени−1,[24] или единицы времени, такие как время удвоения.[25]
не является биологической константой патогена, так как на него также влияют другие факторы, такие как условия окружающей среды и поведение инфицированного населения. более того значения обычно оцениваются на основе математических моделей, а оценочные значения зависят от используемой модели и значений других параметров. Таким образом, значения, приведенные в литературе, имеют смысл только в данном контексте, и рекомендуется не использовать устаревшие значения или сравнивать значения, основанные на разных моделях.[26] сам по себе не дает оценки того, насколько быстро инфекция распространяется среди населения.
Наиболее важные применения определяют, появляются ли инфекционное заболевание может распространяться среди населения и определять, какую часть населения следует иммунизировать путем вакцинации для искоренения болезни. Обычно используется модели заражения, когда инфекция сможет начать распространяться среди населения, но только если . Как правило, чем больше значение , тем сложнее контролировать эпидемию. Для простых моделей доля населения, которую необходимо эффективно иммунизировать (то есть не восприимчивой к инфекции) для предотвращения устойчивого распространения инфекции, должна быть больше, чем .[27] И наоборот, доля населения, остающаяся восприимчивой к инфекции, в эндемическое равновесие является .
На базовое количество репродукций влияет несколько факторов, в том числе продолжительность заразительность пораженных людей, заразность микроорганизм, а также количество восприимчивых людей в популяции, с которыми контактируют инфицированные.
История
Корни основной концепции воспроизводства можно проследить через работу Рональд Росс, Альфред Лотка и другие,[28] но его первое современное применение в эпидемиологии было Джорджем Макдональдом в 1952 г.,[29] кто построил популяционные модели распространения малярия. В своей работе он назвал количественную базовую скорость воспроизводства и обозначил ее как . Обозначение величины ставкой может ввести в заблуждение, поскольку в таком случае «ставка» может быть неверно интерпретирована как число в единицу времени. "Число" или "соотношение" теперь предпочтительнее.
Определения в конкретных случаях
Частота контактов и инфекционный период
Предположим, что у инфекционных особей в среднем инфицированных контактов в единицу времени, со средним инфекционным периодом . Тогда базовый номер репродукции:
Эта простая формула предлагает разные способы уменьшения и в конечном итоге распространение инфекции. Можно уменьшить количество контактов, вызывающих инфекцию в единицу времени за счет уменьшения количества контактов в единицу времени (например, оставаясь дома, если для распространения инфекции требуется контакт с другими людьми) или доли контактов, вызывающих инфекцию (например, ношение какого-либо защитного снаряжения). Также возможно уменьшение инфекционного периода. путем обнаружения, а затем изоляции, лечения или уничтожения (как это часто бывает с животными) инфекционных лиц в кратчайшие сроки.
С разными латентными периодами
Скрытый период - это время перехода между событием заражения и проявлением болезни. В случае заболеваний с различными латентными периодами базовое число воспроизводств можно рассчитать как сумму чисел воспроизводства для каждого времени перехода в болезнь. Примером этого является туберкулез (ТБ). Блауэр и соавторы вычислили на простой модели TB следующее репродуктивное число:[30]
В их модели предполагается, что у инфицированных людей может развиться активный туберкулез в результате либо прямого прогрессирования (заболевание развивается сразу после заражения), рассматриваемого выше как БЫСТРЫЙ туберкулез, либо эндогенной реактивации (заболевание развивается через годы после заражения), рассматриваемого выше как МЕДЛЕННЫЙ туберкулез.[31]
Гетерогенные популяции
В популяциях, которые не являются однородными, определение более тонкий. Определение должно учитывать тот факт, что типичный инфицированный человек может не быть обычным человеком. В качестве крайнего примера рассмотрим популяцию, в которой небольшая часть особей полностью смешивается друг с другом, а остальные особи изолированы. Заболевание может распространяться в полностью смешанной части, даже если случайным образом выбранный индивидуум может вызвать менее одного вторичного случая. Это связано с тем, что типичный инфицированный человек находится в полностью смешанной части и, таким образом, может успешно вызывать инфекции. В целом, если люди, инфицированные на ранней стадии эпидемии, в среднем либо более, либо менее вероятно передают инфекцию, чем люди, инфицированные на поздних стадиях эпидемии, то вычисление необходимо учитывать эту разницу. Подходящее определение для в данном случае это «ожидаемое количество вторичных случаев, вызванных типичным инфицированным человеком в начале эпидемии».[32]
Основное число репродуктивных может быть вычислено как отношение известных показателей с течением времени: если заразный человек контактирует с другими людьми в единицу времени, если предполагается, что все эти люди заразились болезнью, и если болезнь имеет средний инфекционный период 1 / γ, то базовое число воспроизведения просто р0 = β/γ. Некоторые заболевания имеют несколько возможных латентных периодов, и в этом случае число воспроизводств для болезни в целом является суммой числа воспроизводств для каждого времени перехода в болезнь. Например, Blower et al.[33] смоделируйте две формы туберкулезной инфекции: в быстром случае симптомы проявляются сразу после заражения; в медленном случае симптомы развиваются спустя годы после первоначального воздействия (эндогенная реактивация). Общее число воспроизводимых - это сумма двух форм сокращения: р0 = р0БЫСТРЫЙ + р0МЕДЛЕННЫЙ.
Методы оценки
Базовое количество воспроизведений можно оценить, изучив детальные цепочки передачи или геномное секвенирование. Однако чаще всего он рассчитывается с использованием эпидемиологических моделей.[34] Во время эпидемии обычно количество диагностированных инфекций через некоторое время известен. На ранних стадиях эпидемии рост является экспоненциальным, с логарифмической скоростью роста.
Для экспоненциального роста может интерпретироваться как совокупное количество диагнозов (включая выздоровевших) или текущее количество случаев инфекции; логарифмическая скорость роста одинакова для обоих определений. Чтобы оценить необходимы предположения о временном промежутке между заражением и постановкой диагноза и времени между заражением и началом заразного развития.
При экспоненциальном росте относится к время удвоения в качестве
Простая модель
Если человек после заражения заражает именно новые люди только спустя ровно время (серийный интервал) прошел, то количество заразных особей со временем растет по мере того, как
Основное дифференциальное уравнение согласования:
или же
В этом случае, или же .
Например, с и , мы бы нашли .
Если зависит от времени
показывая, что может быть важно сохранить ниже 0, усредненное по времени, чтобы избежать экспоненциального роста.
Скрытый инфекционный период, изоляция после постановки диагноза
В этой модели индивидуальное заражение имеет следующие стадии:
- Выявлено: человек инфицирован, но не имеет симптомов и еще не заражает других. Средняя продолжительность экспонированного состояния составляет .
- Скрытая инфекция: человек инфицирован, не имеет симптомов, но заражает других. Средняя продолжительность скрытого инфекционного состояния составляет . Человек заражает другие лица в этот период.
- изоляция после постановки диагноза: принимаются меры для предотвращения дальнейшего заражения, например, путем изоляции инфицированного человека.
Это SEIR модель и можно записать в следующей форме[35]
Этот метод оценки был применен к COVID-19 и ОРВИ. Из дифференциального уравнения для количества облученных лиц следует и количество скрытых инфекционных особей ,
Самый большой собственное значение матрицы - логарифмическая скорость роста , который можно решить за .
В частном случае , эта модель приводит к , который отличается от простая модель над (). Например, с одинаковыми значениями и , мы бы нашли , а не истинное значение . Разница обусловлена незначительной разницей в базовой модели роста; приведенное выше матричное уравнение предполагает, что недавно инфицированные пациенты уже вносят свой вклад в инфекции, в то время как на самом деле инфекции возникают только из-за количества инфицированных в назад. Более правильное лечение потребует использования дифференциальные уравнения с запаздыванием.[36]
Число эффективных репродукций
В действительности, различные доли населения в любой момент времени обладают иммунитетом к любой болезни. Чтобы учесть это, эффективное репродуктивное число используется, обычно записывается как , или среднее количество новых инфекций, вызванных одним инфицированным человеком за раз т у частично восприимчивого населения. Его можно найти, умножив дробью S восприимчивого населения. Когда доля населения, обладающего иммунитетом, увеличивается (т. Е. Восприимчивое население S уменьшается) настолько, что падает ниже 1 ",коллективный иммунитет«достигнута, и количество заболевших среди населения будет постепенно уменьшаться до нуля.[37][38][39]
Ограничения р0
Использование в популярной прессе привело к недопониманию и искажению его значения. можно рассчитать из множества различных математические модели. Каждый из них может дать различную оценку , который необходимо интерпретировать в контексте этой модели. Следовательно, заразность различных возбудителей инфекций невозможно сравнивать без пересчета. с инвариантными предположениями. значения для прошлых вспышек могут быть недействительными для текущих вспышек того же заболевания. Вообще говоря, может использоваться как порог, даже если рассчитывается разными методами: если , вспышка погаснет, и если , вспышка будет расширяться. В некоторых случаях для некоторых моделей значения может по-прежнему приводить к самовоспроизводящимся вспышкам. Это особенно проблематично, если между хостами существуют промежуточные векторы, такие как малярия.[40] Таким образом, сравнения значений из "Значения Таблицу общеизвестных инфекционных болезней »следует вести с осторожностью.
Несмотря на то что не может быть изменен путем вакцинации или других изменений в восприимчивости населения, он может варьироваться в зависимости от ряда биологических, социально-поведенческих и экологических факторов.[26] Его также можно изменить с помощью физического дистанцирования и других мер государственной политики или социального вмешательства,[41][26] хотя некоторые исторические определения исключают любое преднамеренное вмешательство в снижение передачи заболевания, включая нефармакологические вмешательства.[22] И действительно, включены ли нефармакологические вмешательства в часто зависит от бумаги, болезни и того, что, если какое-либо вмешательство изучается.[26] Это создает некоторую путаницу, потому что не является константой; тогда как большинство математических параметров с индексами "ноль" являются константами.
зависит от многих факторов, многие из которых необходимо оценить. Каждый из этих факторов увеличивает неопределенность оценок . Многие из этих факторов не важны для информирования государственной политики. Следовательно, государственная политика может быть лучше обслужена метриками, аналогичными , но которые проще оценить, например время удвоения или же период полураспада (т1⁄2).[42][43]
Методы, используемые для расчета включить функция выживания, переставляя самые большие собственное значение из Матрица якобиана, метод следующего поколения,[44] расчеты по собственной скорости роста,[45] наличие эндемического равновесия, количество восприимчивых к эндемическому равновесию, средний возраст заражения[46] и окончательное уравнение размера. Некоторые из этих методов согласуются друг с другом, даже если исходить из одной и той же системы. дифференциальные уравнения.[40] Еще меньше людей фактически подсчитывают среднее количество вторичных инфекций. С редко наблюдается в полевых условиях и обычно рассчитывается с помощью математической модели, что сильно ограничивает его полезность.[47]
В популярной культуре
В фильме 2011 года Заражение, художественный триллер о медицинских катастрофах, расчеты блоггера для представлены, чтобы отразить прогрессирование смертельной вирусной инфекции от тематических исследований до пандемии. Изображенные методы были ошибочными.[41]
Смотрите также
Примечания
- Компартментные модели в эпидемиологии описать динамику заболевания во времени в популяции восприимчивых (S), инфекционных (I) и выздоровевших (R) людей, используя модель SIR. Обратите внимание, что в модели SIR и - разные количества - первая описывает количество восстановленных т = 0, тогда как последний описывает отношение частоты контактов к частоте восстановления.
- По данным Провинциального центра по контролю и профилактике заболеваний Гуандун, «эффективное репродуктивное число (R или Rе[48]) чаще используется для описания передаваемости, которая определяется как среднее количество вторичных наблюдений, генерируемых за [sic] инфекционный случай ». Например, по предварительной оценке во время продолжающейся пандемии, эффективное репродуктивное число для SARS-CoV-2 оказалось 2,9,[нужна цитата] тогда как для SARS это было 1,77.
Рекомендации
- ^ Если не указано иное значения от История и эпидемиология глобальной ликвидации оспы (В архиве 2016-05-10 в Wayback Machine), модуль учебного курса «Оспа: болезнь, профилактика, вмешательство». CDC и Всемирная организация здоровья, 2001. Slide 17. Это дает исходники как "Изменено из Epid Rev 1993;15: 265-302, Am J Prev Med 2001; 20 (4S): 88-153, MMWR 2000; 49 (СС-9); 27-38 "
- ^ Guerra, Fiona M .; Болотин, Шелли; Лим, Джиллиан; Хеффернан, Джейн; Дикс, Шелли Л .; Ли, Е; Кроукрофт, Наташа С. (1 декабря 2017 г.). «Базовое репродуктивное число (R0) кори: систематический обзор». Ланцетные инфекционные болезни. 17 (12): e420 – e428. Дои:10.1016 / S1473-3099 (17) 30307-9. ISSN 1473-3099. PMID 28757186. Получено 18 марта, 2020.
- ^ Служба здравоохранения Ирландии. Информация для медицинских работников (PDF). Получено 27 марта, 2020.
- ^ Министерство здравоохранения Австралии Описание лабораторного случая эпидемического паротита (ЖКД)
- ^ Айзенберг, Джозеф (12 февраля 2020 г.). «R0: Как ученые количественно определяют интенсивность вспышки коронавируса и ее пандемический потенциал». sph.umich.edu. Получено 4 сентября, 2020.
- ^ Вайсбергер, Минди (8 февраля 2019 г.). «Это одно число показывает, почему корь распространяется как лесной пожар». livescience.com. Получено 4 сентября, 2020.
- ^ Кречмар М., Теунис П.Ф., Пебоди Р.Г. (2010). «Заболеваемость и воспроизводимость коклюша: оценки на основе данных серологических и социальных контактов в пяти европейских странах». PLOS Med. 7 (6): e1000291. Дои:10.1371 / journal.pmed.1000291. ЧВК 2889930. PMID 20585374.
- ^ Гани, Раймонд; Лич, Стив (декабрь 2001 г.). «Потенциал передачи оспы среди современного населения». Природа. 414 (6865): 748–751. Дои:10.1038 / 414748a. ISSN 1476-4687. PMID 11742399. S2CID 52799168. Получено 18 марта, 2020.
- ^ Човелл Г., Кастильо-Чавес С., Фенимор П.В., Крибс-Залета С.М., Арриола Л., Хайман Дж. М. (2004). «Параметры модели и борьба со вспышками SARS». Emerg Infect Dis. 10 (7): 1258‐1263. Дои:10.3201 / eid1007.030647. ЧВК 3323341. PMID 15324546.
- ^ Prather KA, Marr LC, Schooley RT и др. (16 октября 2020 г.). «Бортовая передача SARS-CoV-2» (PDF). Наука. 370 (6514): 303–304. Дои:10.1126 / science.abf0521. В архиве с оригинала 5 октября 2020 г.. Получено 30 октября, 2020.
- ^ Sanche, S .; Лин, Ю. Т .; Xu, C .; Romero-Severson, E .; Hengartner, E .; Кэ, Р. (июль 2020 г.). «Высокая заразность и быстрое распространение тяжелого острого респираторного синдрома, вызванного коронавирусом 2». Возникающие инфекционные заболевания. 26 (7): 1470–1477. Дои:10.3201 / eid2607.200282. ЧВК 7323562. PMID 32255761.
- ^ «Новый вирус короны - Информация для врачей» (PDF). Правительство Австралии - Департамент Хитла. 6 июля 2020 г.
- ^ Фриман, Колин. «Волшебная формула, которая определит, победят ли Эбола». Телеграф. Telegraph.Co.Uk. Получено 30 марта, 2020.
- ^ Truelove, Shaun A .; Киган, Линдси Т .; Мосс, Уильям Дж .; Chaisson, Lelia H .; Машер, Эмили; Азман, Андрей С .; Лесслер, Джастин (2019). «Клинические и эпидемиологические аспекты дифтерии: систематический обзор и объединенный анализ». Клинические инфекционные болезни. 71 (1): 89–97. Дои:10.1093 / cid / ciz808. ЧВК 7312233. PMID 31425581.
- ^ Фергюсон Н.М.; Каммингс Д.А.; Fraser C; Cajka JC; Cooley PC; Берк Д.С. (2006). «Стратегии смягчения последствий пандемии гриппа». Природа. 442 (7101): 448–452. Bibcode:2006Натура.442..448F. Дои:10.1038 / природа04795. ЧВК 7095311. PMID 16642006.
- ^ Хан, Аднан; Навид, Махим; Дур-э-Ахмад, Мухаммад; Имран, Мудассар (24 февраля 2015 г.). «Оценка базового репродуктивного коэффициента во время вспышки Эболы в Либерии и Сьерра-Леоне». Инфекционные болезни бедности. 4: 13. Дои:10.1186 / s40249-015-0043-3. ISSN 2049-9957. ЧВК 4347917. PMID 25737782.
- ^ а б Фрейзер, Кристоф; Donnelly, Christl A .; Кошемез, Саймон; Hanage, Уильям П .; Ван Керхове, Мария Д .; Холлингсуорт, Т. Дейрдре; Гриффин, Джейми; Baggaley, Rebecca F .; Jenkins, Helen E .; Лайонс, Эмили Дж .; Жомбарт, Тибо (19 июня 2009 г.). «Пандемический потенциал штамма гриппа A (H1N1): первые результаты». Наука. 324 (5934): 1557–1561. Bibcode:2009Научный ... 324.1557F. Дои:10.1126 / science.1176062. ISSN 0036-8075. ЧВК 3735127. PMID 19433588.
- ^ Coburn BJ; Вагнер Б.Г.; Воздуходувка S (2009 г.). «Моделирование эпидемий и пандемий гриппа: взгляд на будущее свиного гриппа (H1N1)». BMC Медицина. 7. Статья 30. Дои:10.1186/1741-7015-7-30. ЧВК 2715422. PMID 19545404.
- ^ Кухарский, Адам; Альтхаус, Кристиан Л. (2015). «Роль сверхраспространения в передаче коронавируса ближневосточного респираторного синдрома (БВРС-КоВ)». Евронаблюдение. 20 (26): 14–8. Дои:10.2807 / 1560-7917.ES2015.20.25.21167. PMID 26132768.
- ^ https://edisciplinas.usp.br/pluginfile.php/4483966/mod_folder/content/0/NIPAH%20V%C3%8DRUS.pdf?forcedownload=1
- ^ Миллиган, Грегг Н .; Барретт, Алан Д. Т. (2015). Вакцинология: важное руководство. Чичестер, Западный Сассекс: Уайли Блэквелл. п. 310. ISBN 978-1-118-63652-7. OCLC 881386962.
- ^ а б Беккер, Нильс Дж .; Гласс, Кэтрин; Барнс, Белинда; Кэли, Питер; Филп, Дэвид; Маккоу, Джеймс; Маквернон, Джоди; Вуд, Джеймс (апрель 2006 г.). "Номер репродукции". Использование математических моделей для оценки реакции на вспышку вирусного респираторного заболевания. Национальный центр эпидемиологии и здоровья населения. ISBN 1-74186-357-0. Получено 1 февраля, 2020.
- ^ Адам, Дэвид (2020). «Руководство по R - неправильно понятой метрике пандемии». Природа. 583: 346–348. Дои:10.1038 / d41586-020-02009-w.
- ^ Джонс, Джеймс. «Заметки о R0» (PDF). Стэндфордский Университет.
- ^ Сигел, Итан. «Почему« экспоненциальный рост »так страшен коронавирусу COVID-19». Forbes. Получено 19 марта, 2020.
- ^ а б c d Delamater, Paul L .; Street, Erica J .; Лесли, Тимоти Ф .; Ян, Ю. Тони; Якобсен, Кэтрин Х. (январь 2019 г.). «Сложность базового репродуктивного числа (R 0)». Возникающие инфекционные заболевания. 25 (1): 1–4. Дои:10.3201 / eid2501.171901. ISSN 1080-6040. ЧВК 6302597. PMID 30560777.
- ^ Хорошо, Пол; Имс, Кен; Хейманн, Дэвид Л. (1 апреля 2011 г.). ""Иммунитет стада ": грубый справочник". Клинические инфекционные болезни. 52 (7): 911–916. Дои:10.1093 / cid / cir007. ISSN 1058-4838. PMID 21427399.
- ^ Смит, Дэвид Л .; Битва, Кэтрин Е .; Hay, Simon I .; Баркер, Кристофер М .; Скотт, Томас У .; Маккензи, Ф. Эллис (5 апреля 2012 г.). "Росс, Макдональд и теория динамики и контроля патогенов, передаваемых комарами". Патогены PLOS. 8 (4): e1002588. Дои:10.1371 / journal.ppat.1002588. ISSN 1553-7366. ЧВК 3320609. PMID 22496640.
- ^ Макдональд, Г. (сентябрь 1952 г.). «Анализ равновесия при малярии». Бюллетень по тропическим болезням. 49 (9): 813–829. ISSN 0041-3240. PMID 12995455.
- ^ Блоуер, С. М .; Mclean, A.R .; Porco, T. C .; Смолл, П. М .; Hopewell, P.C .; Санчес, М.А. (1995). «Динамика внутренней передачи эпидемии туберкулеза». Природа Медицина. 1 (8): 815–821. Дои:10,1038 / нм0895-815. PMID 7585186. S2CID 19795498.
- ^ Ма Y, Хорсбург CR, White LF, Jenkins HE (сентябрь 2018 г.). «Количественная оценка передачи туберкулеза: систематический обзор репродуктивного числа и серийных интервалов оценки туберкулеза». Эпидемиол Инфекция. 146 (12): 1478–1494. Дои:10.1017 / S0950268818001760. ЧВК 6092233. PMID 29970199.
- ^ О Дикманн; J.A.P. Хестербек; J.A.J. Мец (1990). «Об определении и расчете базового коэффициента воспроизводства в моделях инфекционных заболеваний в гетерогенных популяциях ». Журнал математической биологии. 28 (4): 356–382. Дои:10.1007 / BF00178324. HDL:1874/8051. PMID 2117040. S2CID 22275430.
- ^ Блауэр, С. М., Маклин, А. Р., Порко, Т. К., Смолл, П. М., Хоупуэлл, П. К., Санчес, М. А. и др. (1995). «Внутренняя динамика передачи эпидемии туберкулеза». Природа Медицина, 1, 815–821.
- ^ Уол, Ширли; Шаффнер, Стивен Ф .; Сабети, Пардис К. (2016). «Геномный анализ вирусных вспышек». Ежегодный обзор вирусологии. 3 (1): 173–195. Дои:10.1146 / annurev-virology-110615-035747. ЧВК 5210220. PMID 27501264.
- ^ Липсич, Марк; Коэн, Тед; Купер, Бен; Робинс, Джеймс М .; Ма, Стефан; Джеймс, Лин; Гопалакришна, Гоури; Чу, Суок Кай; Тан, Чор Чуан; Самор, Мэтью H .; Фисман, Дэвид (20 июня 2003 г.). «Динамика передачи и контроль тяжелого острого респираторного синдрома». Наука. 300 (5627): 1966–1970. Bibcode:2003Sci ... 300.1966L. Дои:10.1126 / science.1086616. ISSN 0036-8075. ЧВК 2760158. PMID 12766207.
- ^ Rihan, Fathalla A .; Анвар, М. Наим (2012). «Качественный анализ модели отложенной эпидемии SIR с высоким уровнем заболеваемости». Международный журнал дифференциальных уравнений. 2012: 1–13. Дои:10.1155/2012/408637. ISSN 1687-9643.
- ^ Гарнетт, Г. П. (1 февраля 2005 г.). «Роль коллективного иммунитета в определении эффекта вакцин против заболеваний, передающихся половым путем». Журнал инфекционных болезней. 191 (Приложение 1): S97–106. Дои:10.1086/425271. PMID 15627236.
- ^ Rodpothong, P; Ауеваракул, П (2012). «Вирусная эволюция и эффективность передачи». Всемирный журнал вирусологии. 1 (5): 131–34. Дои:10.5501 / wjv.v1.i5.131. ЧВК 3782273. PMID 24175217.
- ^ Даббагян, В .; Маго, В. К. (2013). Теории и моделирование сложных социальных систем. Springer. С. 134–35. ISBN 978-3642391491. Получено 29 марта, 2015.
- ^ а б Ли Дж., Блейкли Д., Смит? RJ (2011). "Провал ". Вычислительные и математические методы в медицине. 2011 (527610): 1–17. Дои:10.1155/2011/527610. ЧВК 3157160. PMID 21860658.
- ^ а б Бирн, Майкл (6 октября 2014 г.), «Неправильно понятый номер, который предсказывает эпидемии», Vice.com, получено 23 марта, 2020
- ^ Balkew, Teshome Mogessie (декабрь 2010 г.). Модель SIR, когда S (t) - многоэкспоненциальная функция (Тезис). Государственный университет Восточного Теннесси.
- ^ Ирландия, MW, изд. (1928). Медицинский департамент армии США во время мировой войны, т. IX: Инфекционные и другие болезни. Вашингтон: США: Типография правительства США. С. 116–7.
- ^ Дикманн О., Хестербик Дж. А. (2000). «Базовый коэффициент воспроизводства». Математическая эпидемиология инфекционных заболеваний: построение модели, анализ и интерпретация. Нью-Йорк: Вили. С. 73–98. ISBN 0-471-49241-8.
- ^ Човелл Г., Хенгартнерб Н.В., Кастильо-Чавеза С., Фенимореа П.В., Хайман Дж. М. (2004). «Базовое репродуктивное число Эболы и последствия мер общественного здравоохранения: случаи Конго и Уганды». Журнал теоретической биологии. 229 (1): 119–126. arXiv:q-bio / 0503006. Дои:10.1016 / j.jtbi.2004.03.006. PMID 15178190. S2CID 7298792.
- ^ Ajelli M; Iannelli M; Манфреди П и Чофи дельи Атти, ML (2008). «Основные математические модели временной динамики ВГА в районах Италии со средней эндемичностью». Вакцина. 26 (13): 1697–1707. Дои:10.1016 / j.vaccine.2007.12.058. PMID 18314231.
- ^ Хеффернан Дж. М., Смит Р. Дж., Уол Л. М. (2005). «Перспективы базового коэффициента воспроизводства». Журнал интерфейса Королевского общества. 2 (4): 281–93. Дои:10.1098 / rsif.2005.0042. ЧВК 1578275. PMID 16849186.
- ^ Хелд, Леонард; Хенс, Ниль; О'Нил, Филип Д .; Валлинга, Жакко (7 ноября 2019 г.). Справочник по анализу данных по инфекционным заболеваниям. CRC Press. п. 347. ISBN 978-1-351-83932-7.
дальнейшее чтение
| Scholia имеет профиль для базовый номер репродукции (Q901464). |
- Heesterbeek, J.A.P. (2002). "Краткая история и рецепт его расчета ». Acta Biotheoretica. 50 (3): 189–204. Дои:10.1023 / А: 1016599411804. PMID 12211331. S2CID 10178944.
- Heffernan, J.M .; Smith, R.J .; Wahl, L.M. (октябрь 2005 г.). «Перспективы базового репродуктивного соотношения». Журнал интерфейса Королевского общества. 2 (4): 281–293. Дои:10.1098 / rsif.2005.0042. ЧВК 1578275. PMID 16849186.
- Джонс, Джеймс Холланд (1 мая 2007 г.). "Примечания к " (PDF). Получено 6 ноября, 2018.
- Van Den Driessche, P .; Уотмо, Джеймс (2008). «Дополнительные примечания к основному репродуктивному номеру». Математическая эпидемиология. Конспект лекций по математике. 1945. С. 159–178. Дои:10.1007/978-3-540-78911-6_6. ISBN 978-3-540-78910-9.