WikiDer > Биплот
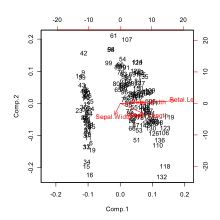

Биплоты - это тип исследовательского графа, используемый в статистика, обобщение простого двухпеременного диаграмма рассеяния. Диаграмма позволяет получить информацию как по образцы и переменные матрица данных для графического отображения. Образцы отображаются в виде точек, а переменные отображаются в виде векторов, линейных топоры или нелинейные траектории. В случае категориальных переменных баллы уровня категории может использоваться для представления уровней категориальной переменной. А обобщенный biplot отображает информацию как о непрерывных, так и о категориальных переменных.
Введение и история
Этот раздел может требовать уборка встретиться с Википедией стандарты качества. Конкретная проблема: Трудно понять, в основном содержит оглавление двух разных книг. (Ноябрь 2020) (Узнайте, как и когда удалить этот шаблон сообщения) |
Биплот был представлен К. Рубен Габриэль (1971).[1] Гауэр и Хэнд (1996) написали монографию о биплотах. Ян и Канг (2003) описали различные методы, которые можно использовать для визуализации и интерпретации двумерного графика. Книга Гринакра (2010)[2] представляет собой практическое руководство по биплотам, ориентированное на пользователя, вместе со сценариями в открытом доступе Язык программирования R, для создания биплотов, связанных с Анализ главных компонентов (PCA), многомерное масштабирование (MDS), логарифмический анализ (LRA), также известный как спектральное отображение[3][4]—дискриминантный анализ (DA) и различные формы анализ корреспонденции: простой анализ соответствий (CA), анализ множественных соответствий (MCA) и анализ канонических соответствий (CCA) (Greenacre 2016[5]). Книга Гауэра, Люббе и Ле Ру (2011) направлена на популяризацию биплотов как полезного и надежного метода визуализации многомерных данных, когда исследователи хотят рассмотреть, например, анализ главных компонентов (PCA), анализ канонических переменных (CVA). или различные виды анализа соответствий.
Строительство
Биплот строится с использованием разложение по сингулярным числам (СВД) для получения приближение низкого ранга к преобразованной версии матрицы данных Икс, чей п строки - это образцы (также называемые случаями или объектами), и чьи п столбцы - это переменные. Преобразованная матрица данных Y получается из исходной матрицы Икс центрированием и, при необходимости, стандартизацией столбцов (переменных). Используя СВД, мы можем написать Y = ∑k=1,...пdkтыkvkТ;, где тыk находятся п-мерные векторы-столбцы, vk находятся п-мерные векторы-столбцы, а dk представляют собой невозрастающую последовательность неотрицательных скаляры. Двухуровневый график формируется из двух графиков рассеяния, которые имеют общий набор осей и имеют промежуточный набор скалярное произведение интерпретация. Первая диаграмма рассеяния формируется из точек (d1αты1я, d2αты2я), за я = 1,...,п. Второй участок формируется из точек (d11 − αv1j, d21 − αv2j), за j = 1,...,п. Это двумерный график, образованный двумя доминирующими членами SVD, который затем может быть представлен на двумерном дисплее. Типичный выбор α - это 1 (чтобы дать интерпретацию расстояния для отображения строки) и 0 (чтобы дать интерпретацию расстояния для отображения столбца), а в некоторых редких случаях α = 1/2 для получения симметрично масштабируемого двоичного графика (что дает нет интерпретации расстояния для строк или столбцов, а только интерпретация скалярного произведения). Набор точек, изображающих переменные, можно нарисовать в виде стрелок от начала координат, чтобы укрепить идею о том, что они представляют собой оси двух графиков, на которые можно проецировать образцы для аппроксимации исходных данных.
Рекомендации
- ^ Габриэль, К. Р. (1971). Двухслойное графическое отображение матриц с приложением к анализу главных компонентов. Биометрика, 58(3), 453–467.
- ^ Гринакр, М. (2010). Биплоты на практике. Фонд BBVA, Бильбао, Испания. Доступно бесплатно на http://www.multivariatestatistics.org
- ^ Леви, Пол Дж. (2005). «Спектральное отображение, личный и исторический отчет о приключении в многомерном анализе данных». Хемометрия и интеллектуальные лабораторные системы. 77 (1–2): 215–223. Дои:10.1016 / j.chemolab.2004.07.010.
- ^ Дэвид Ливингстон (2009). Практическое руководство по анализу научных данных. Чичестер, John Wiley & Sons Ltd, 233–238. ISBN 978-0-470-85153-1
- ^ Гринакр, М. (2016) Анализ корреспонденции на практике. Третье издание. Чепмен и Холл / CRC Press.ISBN 978-84-923846-8-6
Источники
- Габриэль, К. (1971). «Двухслойное графическое отображение матриц с приложением к анализу главных компонент». Биометрика. 58 (3): 453–467. Дои:10.1093 / biomet / 58.3.453.
- Гауэр, Дж. К., Люббе, С., Ле Ру, Н. (2010). Понимание биплотов. Wiley. ISBN 978-0-470-01255-0
- Гауэр, Дж. К. и Хэнд, Д. Дж. (1996). Биплоты. Чепмен и Холл, Лондон, Великобритания. ISBN 0-412-71630-5
- Ян В. и Канг М.С. (2003). Анализ двух графиков GGE. CRC Press, Бока-Ратон, Флорида. ISBN 0-8493-1338-4
- Демей, Дж. Р., Висенте-Вильярдон, Дж. Л., Галиндо-Вильярдон, М. и Замбрано, А. (2008). Определение молекулярных маркеров, связанных с классификацией генотипов с помощью внешних логистических биплотов. Биоинформатика. 24(24):2832–2838
