WikiDer > Прыгающий мяч

Bouncing ball
О шарах, называемых «надувные шары», см. прыгучий мяч. Чтобы узнать об устройстве, используемом при видеозаписи для обозначения ритма песни, см. прыгающий мяч (музыка). Информацию о компьютерном вирусе см. Прыгающий мяч (вирус).

Прыгающий мяч. Движение не совсем параболический из-за сопротивление воздуха.

В физика прыгающего мяча касается физического поведения подпрыгивая мячи, особенно его движение до, во время и после влияние против поверхности другого тело. Некоторые аспекты поведения прыгающего мяча служат введением в механика в Средняя школа или же студент курсы физики уровня. Однако точное моделирование поведения сложно и интересно спортивная инженерия.

Движение шара обычно описывается движение снаряда (на который может повлиять сила тяжести, тащить, то Эффект Магнуса, и плавучесть), тогда как его влияние обычно характеризуется коэффициент реституции (на который может влиять природа мяча, характер поверхности удара, скорость удара, вращение и местные условия, такие как температура и давление). Для обеспечения справедливо, много спортивные руководящие органы установить ограничения на подпрыгиваемость своего мяча и запретить изменение аэродинамических свойств мяча. Подпрыгивание мячей было особенностью спорта, столь же древнего, как Мезоамериканская игра в мяч.[1]

Силы во время полета и влияние на движение

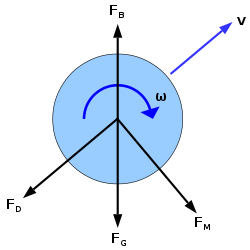
Примечание: В этой статье, векторов выделены жирным шрифтом, а величины и скалярные величины выделены курсивом.
Силы, действующие на вращающийся шар во время его полета, - это сила гравитации (Fграмм), сила сопротивления (FD), Магнус сила (FM), а подъемная сила (FB).

Движение прыгающего мяча подчиняется движение снаряда.[2][3] На настоящий мяч действуют многие силы, а именно сила гравитации (Fграмм), сила сопротивления из-за сопротивление воздуха (FD), Магнус сила из-за мяча вращение (FM), а подъемная сила (FB). В общем, нужно использовать Второй закон Ньютона с учетом всех сил для анализа движения мяча:

куда м масса шара. Здесь, а, v, р представляют мяч ускорение, скорость, и позиция над время т.

Сила тяжести

Основная статья: Сила тяжести
Траектория отскока мяча под углом 70 ° после удара без тащить  , с Стокса сопротивление  , и с Сопротивление Ньютона  .

Сила тяжести направлена ​​вниз и равна[4]

куда м масса шара, а грамм это гравитационное ускорение, который на земной шар варьируется между 9.764 РС2 и 9,834 м / с2.[5] Поскольку другие силы обычно невелики, движение часто бывает идеализированный как находящиеся только под действием силы тяжести. Если на мяч действует только сила тяжести, механическая энергия будет консервированный во время его полета. В этом идеализированном случае уравнения движения имеют вид

куда а, v, и р обозначают ускорение, скорость и положение мяча, а v0 и р0 - начальная скорость и положение мяча соответственно.

В частности, если мяч отскакивает под углом θ с землей, движение в Икс- и у-оси (представляющие горизонтальный и вертикальный движение соответственно) описывается[6]

Из уравнений следует, что максимальная высота (ЧАС) и классифицировать (р) и время полета (Т) шара, отскакивающего от плоской поверхности, даются[2][6]

Дальнейшие уточнения к движению мяча можно внести с учетом сопротивление воздуха (и связанные эффекты, такие как тащить и ветер), Эффект Магнуса, и плавучесть. Поскольку более легкие шары ускоряются быстрее, на их движение, как правило, больше влияют такие силы.

Тащить

Основная статья: Перетащите (физика)

Воздушный поток вокруг мяча может быть либо ламинарный или же бурный в зависимости от Число Рейнольдса (Re), определяемый как:

куда ρ это плотность воздуха, μ в динамическая вязкость воздуха, D диаметр мяча, и v скорость полета мяча в воздухе. На температура из 20 ° C, ρ = 1,2 кг / м3 и μ = 1.8×10−5 Па · с.[7]

Если число Рейнольдса очень низкое (Re <1), сила сопротивления шара описывается выражением Закон Стокса:[8]

куда р - радиус шара. Эта сила действует против направления мяча (в направлении ). Однако для большинства спортивных мячей число Рейнольдса будет между 10.4 и 105 и закон Стокса не применяется.[9] При этих более высоких значениях числа Рейнольдса сила сопротивления шара вместо этого описывается уравнение сопротивления:[10]

куда Cd это коэффициент трения, и А в площадь поперечного сечения мяча.

Перетаскивание приведет к потере механической энергии мяча во время полета и уменьшит его дальность и высоту, в то время как боковой ветер отклонит его от первоначального пути. Оба эффекта должны быть приняты во внимание игроками, занимающимися такими видами спорта, как гольф.

Эффект Магнуса

Основная статья: Эффект Магнуса
Сила Магнуса, действующая на шар с обратное вращение. Фигурные линии потока представляют собой бурный будить. Воздушный поток отклоняется в сторону вращения.
Топспин для настольного тенниса
Обратное вращение для настольного тенниса
В настольный теннис, опытный игрок может использовать вращение мяча, чтобы повлиять на его траекторию. во время полета и это реакция при ударе с поверхностью. С вершина, мяч достигает максимальной высоты по мере полета (1), а затем резко изгибается вниз (2). Удар толкает мяч вперед (3) и будет стремиться отскочить вверх при ударе по мячу соперника. весло. Ситуация обратная в случае обратное вращение.

В вращение мяча повлияет на его траекторию через Эффект Магнуса. Согласно Теорема Кутты – Жуковского., для вращающейся сферы с невязкий поток воздуха сила Магнуса равна[11]

куда р - радиус шара, ω в угловая скорость (или скорость вращения) мяча, ρ плотность воздуха, и v скорость мяча относительно воздуха. Эта сила направлена ​​перпендикулярно движению и перпендикулярно оси вращения (в направлении ). Сила направлена ​​вверх для обратного вращения и вниз для верхнего вращения. На самом деле течение никогда не бывает гладким, и подъем Магнуса лучше описать[12]

куда ρ плотность воздуха, CL в коэффициент подъема, А площадь поперечного сечения мяча, и v скорость мяча относительно воздуха. Коэффициент подъемной силы - это комплексный фактор, который зависит, помимо прочего, от соотношения rω/v, число Рейнольдса и шероховатость поверхности.[12] В определенных условиях коэффициент подъемной силы может быть даже отрицательным, изменяя направление силы Магнуса (обратный эффект Магнуса).[4][13][14]

В спорте вроде теннис или же волейбол, игрок может использовать эффект Магнуса для управления траекторией мяча (например, через вершина или же обратное вращение) во время полета. В гольф, эффект отвечает за нарезка и крючок которые обычно наносят ущерб игроку в гольф, но также помогают увеличить диапазон водить машину и другие кадры.[15][16] В бейсбол, кувшины использовать эффект для создания кривые шары и другие специальные поля.[17]

Подделка мяча часто является незаконным и часто находится в центре внимания крикет споры, такие как споры между Англия и Пакистан в августе 2006 г..[18] В бейсболе термин 'плеваться'относится к незаконному покрытию мяча слюной или другими веществами для изменения аэродинамика мяча.[19]

Плавучесть

Основная статья: Плавучесть

Любой предмет, погруженный в жидкость например, вода или воздух будут испытывать подъем вверх плавучесть.[20] В соответствии с Принцип архимеда, эта выталкивающая сила равна весу жидкости, вытесняемой объектом. В случае шара эта сила равна

Выталкивающая сила обычно мала по сравнению с сопротивлением и силами Магнуса, и ею часто можно пренебречь. Однако в случае с баскетбольным мячом подъемная сила может составлять около 1,5% веса мяча.[20] Поскольку плавучесть направлена ​​вверх, она увеличивает дальность полета и высоту мяча.

Влияние

Сжатие (A → B) и декомпрессия (B → C) удара мяча о поверхность. Сила удара обычно пропорциональна расстоянию сжатия, по крайней мере, для небольших сжатий, и может быть смоделирована как сила пружины.[21][22]
Внешнее видео
значок видео Флориан Корн (2013). «Мяч, подскакивающий в замедленной съемке: резиновый мяч». YouTube.

Когда мяч удары поверхность, поверхность отдачи и вибрирует, как и мяч, создавая оба звук и высокая температура, и мяч проигрывает кинетическая энергия. Кроме того, удар может придать мячу некоторое вращение, передавая часть его поступательная кинетическая энергия в кинетическая энергия вращения. Эта потеря энергии обычно характеризуется (косвенно) через коэффициент реституции (или COR, обозначаемый е):[23][примечание 1]

куда vж и vя - конечная и начальная скорости мяча, а тыж и тыя - конечная и начальная скорости ударов по поверхности соответственно. В конкретном случае, когда мяч ударяется о неподвижную поверхность, COR упрощает

Таким образом, для мяча, упавшего на пол, COR будет варьироваться от 0 (без отскока, полная потеря энергии) до 1 (идеально подскакивает, без потерь энергии). Значение COR ниже 0 или выше 1 теоретически возможно, но будет означать, что мяч пошел через поверхность (е < 0), или что поверхность не «расслаблялась», когда мяч касался ее (е > 1), как и в случае приземления мяча на подпружиненную платформу.

Для анализа вертикальной и горизонтальной составляющих движения COR иногда разделяют на нормальный COR (еу), и касательный COR (еИкс), определяется как[24]

куда р и ω обозначают радиус и угловую скорость шара, а р и Ω обозначают радиус и угловую скорость ударной поверхности (такой как бейсбольная бита). Особенно rω это тангенциальная скорость поверхности шара, а RΩ тангенциальная скорость ударяющей поверхности. Это особенно интересно, когда мяч ударяется о поверхность в наклонный угол, или когда вращение впутан.

Для прямого падения на землю без вращения, когда на мяч действует только сила тяжести, COR можно связать с несколькими другими величинами следующим образом:[22][25]

Здесь, K и U обозначить кинетический и потенциальная энергия мяча, ЧАС максимальная высота мяча, и Т время полета мяча. Индексы «i» и «f» относятся к начальному (до удара) и конечному (после удара) состояниям мяча. Точно так же потеря энергии при ударе может быть связана с COR:

На COR мяча могут влиять несколько факторов, в основном

  • характер поверхности удара (например, трава, бетон, проволочная сетка)[25][26]
  • материал мяча (например, кожа, резина, пластик)[22]
  • давление внутри шара (если он полый)[22]
  • количество вращения, вызванное в шаре при ударе[27]
  • скорость удара[21][22][26][28]

Внешние условия, такие как температура может изменять свойства ударной поверхности или мяча, делая их более гибкими или более жесткими. Это, в свою очередь, повлияет на COR.[22] В общем, мяч будет деформироваться больше при более высоких скоростях удара и, соответственно, потеряет больше своей энергии, уменьшая COR.[22][28]

Вращение и угол удара

Силы, действующие на вращающийся шар во время удара, - это сила притяжения, то нормальная сила, а сила трения (который, как правило, имеет как «поступательный», так и «вращательный» компонент). Если поверхность расположена под углом, сила тяжести будет располагаться под углом к ​​поверхности, а другие силы останутся перпендикулярными или параллельными поверхности.
Внешнее видео
значок видео Биомеханика ММУ (2008). "Удары в гольф - замедленное видео". YouTube.

При ударе о землю некоторые поступательная кинетическая энергия можно преобразовать в кинетическая энергия вращения и наоборот, в зависимости от угла падения мяча и угловой скорости. Если при ударе мяч движется горизонтально, трение будет иметь «поступательный» компонент в направлении, противоположном движению мяча. На рисунке мяч движется к верно, и, следовательно, он будет иметь поступательную составляющую трения, толкающую мяч к оставили. Кроме того, если мяч вращается при ударе, трение будет иметь «вращательную» составляющую в направлении, противоположном вращению мяча. На рисунке мяч вращается по часовой стрелке, а точка, касающаяся земли, движется к оставили по отношению к мячу центр массы. Таким образом, вращательная составляющая трения толкает мяч к верно. В отличие от нормальной силы и силы тяжести, эти силы трения будут вызывать крутящий момент на шаре, и изменить его угловую скорость (ω).[29][30][31][32]

Могут возникнуть три ситуации:[32][33][34]

  1. Если мяч продвигается вперед с обратное вращение, поступательное и вращательное трение действуют в одних и тех же направлениях. Угловая скорость мяча будет уменьшена после удара, как и его горизонтальная скорость, и мяч будет двигаться. вверх, возможно, даже превышающий его первоначальную высоту. Мяч также может начать вращаться в противоположном направлении и даже отскочить назад.
  2. Если мяч продвигается вперед с вершинапоступательное и вращательное трение будут действовать в противоположных направлениях. Что именно происходит, зависит от того, какой из двух компонентов преобладает.
    1. Если мяч вращается намного быстрее, чем он двигался, трение вращения будет преобладать. После удара угловая скорость мяча уменьшится, но его горизонтальная скорость увеличится. Мяч будет двигаться вперед но не будет превышать своей первоначальной высоты и будет продолжать вращаться в том же направлении.
    2. Если мяч движется намного быстрее, чем вращался, преобладает поступательное трение. После удара угловая скорость мяча увеличится, но его горизонтальная скорость уменьшится. Мяч не превысит своей первоначальной высоты и продолжит вращаться в том же направлении.

Если поверхность немного наклонена θ, вся диаграмма будет повернута на θ, но сила тяжести останется направленной вниз (образуя угол θ с поверхностью). Тогда гравитация будет иметь компонент, параллельный поверхности, который будет способствовать трению и, следовательно, вращению.[32]

В ракетка спорт Такие как настольный теннис или же ракетбол, опытные игроки будут использовать спин (в том числе боковое вращение) внезапно изменить направление мяча, когда он ударяется о поверхность, например, о землю или о поверхность соперника. ракетка. Аналогичным образом в крикет, существуют различные методы спин боулинг что может привести к значительному отклонению мяча от подача.

Несферические шары

Силы, действующие на футбольный мяч gridiron или же мяч для регби при ударе находятся сила притяжения, то нормальная сила, а сила трения. Трение обычно имеет «продольный» компонент из-за скорости мяча и «кувыркающего» вращения и «боковой» компонент из-за «осевого» вращения мяча, вызванного броском.

Отскок мяча овальной формы (например, используемых в сетка футбол или же регби) в целом гораздо менее предсказуемо, чем отскок сферического шара. В зависимости от положения мяча при ударе нормальная сила может действовать впереди или позади центр масс мяча, и трение от земли будет зависеть от ориентации мяча, а также от его вращения, вращения и скорости удара. Когда силы, действующие по отношению к центру масс мяча, изменяются по мере того, как мяч катится по земле, и все силы могут оказывать крутящий момент на мяч, включая нормальную силу и силу тяжести. Это может привести к тому, что мяч отскочит вперед, отскочит назад или вбок. Поскольку можно преобразовать некоторую кинетическую энергию вращения в кинетическую энергию поступательного движения, возможно даже, что COR будет больше 1 или скорость движения мяча может увеличиться при ударе.[35]

Множественные уложенные шары

Внешнее видео
значок видео Девушка-физик (2015). "Сложенный шарик". YouTube.

Популярная демонстрация включает отскок нескольких уложенных стопкой шаров. Если теннисный мяч сложен поверх баскетбольного мяча, и оба из них упадут одновременно, теннисный мяч отскочит намного выше, чем при падении сам по себе, даже превышая исходную высоту выброса.[36][37] Результат удивителен, поскольку он явно нарушает закон сохранения энергии.[38] Однако при ближайшем рассмотрении баскетбольный мяч не отскакивает так высоко, как если бы теннисный мяч не находился на нем, и передавал часть своей энергии теннисному мячу, поднимая его на большую высоту.[36]

Обычное объяснение включает рассмотрение двух отдельных ударов: удар баскетбольного мяча об пол и затем удар баскетбольного мяча теннисным мячом.[36][37] Предполагая прекрасно упругие столкновения, баскетбольный мяч, ударяющийся о пол со скоростью 1 м / с, отскочит со скоростью 1 м / с. У теннисного мяча, движущегося со скоростью 1 м / с, будет относительная скорость удара 2 м / с, что означает, что он будет отскакивать со скоростью 2 м / с относительно баскетбольного мяча или 3 м / с относительно пола, и тройной его скорость отскока по сравнению с самим ударом об пол. Это означает, что мяч отскочит от 9 раз его первоначальная высота.[заметка 2]На самом деле из-за неупругие столкновения, теннисный мяч увеличит свою скорость и высоту отскока в меньшем количестве, но все равно будет отскакивать быстрее и выше, чем сам по себе.[37]

Хотя предположения об отдельных ударах на самом деле неверны (шары остаются в тесном контакте друг с другом в течение большей части удара), эта модель, тем не менее, будет воспроизводить экспериментальные результаты с хорошим согласием.[37] и часто используется для понимания более сложных явлений, таких как коллапс ядра из сверхновые,[36] или же маневры гравитационной рогатки.[39]

Спортивные правила

Смотрите также: Регулирование спорта

Несколько спортивные руководящие органы регулировать подвижность мяча различными способами, прямыми и косвенными.

  • AFL: Регулирует манометрическое давление из футбол быть между 62 кПа и 76 кПа.[40]
  • ФИБА: Регулирует манометрическое давление, чтобы баскетбол отскакивает от 1200 мм до 1400 мм (верхняя часть шара) при падении с высоты 1800 мм (нижняя часть шара).[41] Это примерно соответствует COR от 0,727 до 0,806.[заметка 3]
  • ФИФА: Регулирует манометрическое давление футбольный мяч быть между 0.6 банкомат и 1,1 атм в уровень моря (61–111кПа).[42]
  • ФИВБ: Регулирует манометрическое давление волейбол быть между 0.30 кгF/см2 к 0,325 кгF/см2 (От 29,4 до 31,9 кПа) для домашний волейбол, и 0.175 кгF/см2 к 0,225 кгF/см2 (От 17,2 до 22,1 кПа) для пляжный волейбол.[43][44]
  • ITF: Регулирует высоту теннисный мяч отскакивает при падении на «гладкий, жесткий и горизонтальный блок большой массы». Разные типы мячей допускаются для разных типов поверхностей. При падении с высоты 100 дюймов (254 см) отскок должен составлять 54–60 дюймов (137–152 см) для мячей типа 1, 53–58 дюймов (135–147 см) для мячей типа 2 и 3, и 48–53 дюйма (122–135 см) для высотных мячей.[45] Это примерно соответствует COR 0,735–0,775 (мяч типа 1), 0,728–0,762 (шары типов 2 и 3) и 0,693–0,728 (шары для больших высот) при падении на испытательную поверхность.[заметка 3]
  • ITTF: Регулирует игровую поверхность так, чтобы мяч для настольного тенниса отскакивает примерно на 23 см при падении с высоты 30 см.[46] Это примерно соответствует значению COR около 0,876 относительно игровой поверхности.[заметка 3]
  • НБА: Регулирует манометрическое давление баскетбол быть между 7,5 и 8,5psi (От 51,7 до 58,6 кПа).[47]
  • НФЛ: Регулирует манометрическое давление Американский футбол составлять от 12,5 до 13,5 фунтов на кв. дюйм (от 86 до 93 кПа).[48]
  • R&A/USGA: Ограничивает COR мяч для гольфа напрямую, что не должно превышать 0,83 против гольф Клуб.[49]

Давление американского футбола было в центре внимания deflategate полемика.[50][51] Некоторые виды спорта не регулируют прыгающие свойства мячей напрямую, а вместо этого определяют метод конструкции. В бейсбол, введение мяча на пробковой основе помогло положить конец эра мертвого мяча и вызвать эра живого мяча.[52][53]

Смотрите также

Примечания

  1. ^ Здесь, v и ты не просто величина скоростей, но включают также их направление (знак).
  2. ^ Поскольку сохранение механической энергии подразумевает , тогда пропорционально .
  3. ^ а б c Рассчитано с использованием и (если применимо) диаметр мяча. Расчет предполагает, что сопротивление воздуха незначительно.

Рекомендации

  1. ^ Уиттингтон, Э. М., изд. (2001). Спорт жизни и смерти: мезоамериканская игра в мяч. Темза и Гудзон. ISBN 0-500-05108-9.
  2. ^ а б Бранкацио, П. Дж. (1985). «Траектория полета мяча». Учитель физики. 23 (1): 20–23. Bibcode:1985PhTea..23 ... 20Б. Дои:10.1119/1.2341702.
  3. ^ Уокер, Дж. (2014). Основы физики (10-е расширенное изд.). Джон Уайли и сыновья. Рисунок 4-8, стр. 70. ISBN 978-1-118-23072-5.
  4. ^ а б Буш, Дж. У. М. (2013). «Аэродинамика красивой игры» (PDF). В Clanet, К. (ред.). Спортивная физика. Les Éditions de l'École Polytechnique. п. 171. HDL:1721.1/87576. ISBN 978-2-7302-1615-9.
  5. ^ Hirt, C .; Claessens, S .; Fecher, T .; Kuhn, M .; Pail, R .; Рексер, М. (2013). «Новый снимок гравитационного поля Земли в сверхвысоком разрешении». Письма о геофизических исследованиях. 40 (16): 4279–4283. Bibcode:2013GeoRL..40.4279H. Дои:10.1002 / гр.50838.
  6. ^ а б Нейв, Р. «Траектории». Гиперфизика. Получено 2017-01-27.
  7. ^ «Свойства сухого воздуха». Набор инструментов для проектирования. Получено 2017-02-11.
  8. ^ Саутард, Дж. (Осень 2006 г.). «Глава 3: Обтекание сферы II: закон Стокса, уравнение Бернулли, турбулентность, пограничные слои, отрыв потока» (PDF). Специальные темы: Введение в движения жидкости, перенос отложений и создаваемые током осадочные структуры. Массачусетский технологический институт. С. 35–82. Архивировано из оригинал (PDF) на 2017-02-05.
  9. ^ Мета, Р. Д. (2008). «Аэродинамика спортивного мяча». В Nørstrud, H. (ed.). Спортивная аэродинамика. Международный центр механических наук CISM. 506. Springer. С. 229–331. Дои:10.1007/978-3-211-89297-8_12. ISBN 978-3-211-89296-1.
  10. ^ «Перетаскивание шара». НАСА.
  11. ^ «Идеальный подъем вращающегося мяча». НАСА. Получено 2017-02-02.
  12. ^ а б Натан, А. М. (2008). «Влияние вращения на полет бейсбольного мяча» (PDF). Американский журнал физики. 76 (2): 119–124. arXiv:физика / 0605041. Bibcode:2008AmJPh..76..119N. Дои:10.1119/1.2805242. S2CID 15494386.
  13. ^ Kim, J .; Парк, H .; Choi, H .; Ю, Дж. Й. (2011). «Обратный эффект Магнуса на вращающейся сфере» (PDF). 64-е ежегодное собрание отдела гидродинамики APS. Американское физическое общество. Bibcode:2011APS..DFD.A7008K.
  14. ^ Kim, J .; Choi, H .; Парк, H .; Ю, Дж. Й. (2014). «Обратный эффект Магнуса на вращающейся сфере: когда и почему». Журнал гидромеханики. 754: R2. Bibcode:2014JFM ... 754R ... 2K. Дои:10.1017 / jfm.2014.428.
  15. ^ «Эффект Магнуса». HumanKinetics.com. 2008-11-11. Получено 2017-01-27.
  16. ^ ДеФорест, К. (1997). "Почему у мячей для гольфа ямочки?". Оригинальные часто задаваемые вопросы по физике Usenet. Архивировано из оригинал на 2019-07-23. Получено 2017-01-27.
  17. ^ Кланет, К. (2015). «Спортивная баллистика» (PDF). Ежегодный обзор гидромеханики. 47: 455–478. Bibcode:2015АнРФМ..47..455С. Дои:10.1146 / аннурьев-жидкость-010313-141255.
  18. ^ «Инзамам обвиняется МУС». Хранитель. 21 августа 2006 г.. Получено 2017-01-28.
  19. ^ Окрент, Д .; Вульф, С. (1989). Бейсбольные анекдоты. Oxford University Press. п. 89. ISBN 978-0-19-504396-9.
  20. ^ а б Пост, С. (2010). Прикладная и вычислительная механика жидкости. Джонс и Бартлетт Издательство. С. 280–282. ISBN 978-1-934015-47-6.
  21. ^ а б Кросс, Р. (1999). "Отскок мяча" (PDF). Американский журнал физики. 67 (3): 222–227. Bibcode:1999AmJPh..67..222C. Дои:10.1119/1.19229.
  22. ^ а б c d е ж грамм Георгаллас, А .; Ландри, Г. (2016). «Коэффициент восстановления шариков под давлением: механистическая модель». Канадский журнал физики. 94 (1): 42. Bibcode:2016CaJPh..94 ... 42G. Дои:10.1139 / cjp-2015-0378. HDL:1807/69855.
  23. ^ «Коэффициент реституции». RacquetResearch.com. Архивировано из оригинал на 2016-11-23. Получено 2017-01-27.
  24. ^ Крест, R .; Натан, А. М. (2006). «Разброс бейсбольного мяча битой». Американский журнал физики. 74 (10): 896–904. arXiv:физика / 0605040. Bibcode:2006AmJPh..74..896C. Дои:10.1119/1.2209246. S2CID 15488042.
  25. ^ а б Haron, A .; Исмаил, К. А. (2012). «Коэффициент возврата спортивных мячей: нормальное испытание на падение». Серия конференций IOP: Материаловедение и инженерия. 36 (1): 012038. Bibcode:2012MS & E ... 36a2038H. Дои:10.1088 / 1757-899X / 36/1/012038.
  26. ^ а б Кросс, Р. (2000). «Коэффициент возмещения за столкновение счастливых мячей, несчастливых мячей и теннисных мячей» (PDF). Американский журнал физики. 68 (11): 1025–1031. Bibcode:2000AmJPh..68.1025C. Дои:10.1119/1.1285945.
  27. ^ Кросс, Р. (2002). «Поведение прыгающего мяча при захвате-проскальзывании» (PDF). Американский журнал физики. 70 (11): 1093–1102. Bibcode:2002AmJPh..70.1093C. Дои:10.1119/1.1507792.
  28. ^ а б Чжан, X .; Ву-Куок, Л. (2002). «Моделирование зависимости коэффициента восстановления от скорости удара при упругопластических столкновениях». Международный журнал ударной инженерии. 27 (3): 317–341. Дои:10.1016 / S0734-743X (01) 00052-5.
  29. ^ Хессер-Кнолль, М. (2014). «Вращение мяча при отскоке». Физика тенниса. Университет Аляски в Фэрбенксе. Получено 2017-02-01.
  30. ^ Линдси, К. (апрель 2004 г.). «Следуй за прыгающим мячом». Теннисная индустрия. Получено 2017-02-01.
  31. ^ Allen, T .; Haake, S .; Гудвилл, С. (2010). «Влияние трения на удары теннисного мяча». Труды Института инженеров-механиков, часть P. 224 (3): 229–236. Дои:10.1243 / 17543371JSET66.
  32. ^ а б c Кросс, Р. (2005). "Отскок вращающегося шара при нормальном падении" (PDF). Американский журнал физики. 73 (10): 914–920. Bibcode:2005AmJPh..73..914C. Дои:10.1119/1.2008299.
  33. ^ Аллен, Т. (2012). «Мяч в твоей стороне» (PDF). Преимущества ANSYS (Эксклюзивно для сети). Архивировано из оригинал (PDF) на 2017-02-05.
  34. ^ Джафри, С. М. М. (2004). Моделирование динамики удара теннисного мяча с плоской поверхностью. (PDF) (Тезис). Техасский университет A&M. HDL:1969.1/2441.
  35. ^ Кросс, Р. (2011). «Отскок футбольного мяча овальной формы» (PDF). Спортивные технологии. 3 (3): 168–180. Дои:10.1080/19346182.2011.564283. S2CID 108409393.
  36. ^ а б c d Huebner, J. S .; Смит, Т. Л. (1992). «Столкновения нескольких шаров». Учитель физики. 30 (1): 46. Bibcode:1992PhTea..30 ... 46H. Дои:10.1119/1.2343467.
  37. ^ а б c d Кросс, Р. (2007). «Вертикальный отскок двух вертикально расположенных шаров» (PDF). Американский журнал физики. 75 (11): 1009–1016. Bibcode:2007AmJPh..75.1009C. Дои:10.1119/1.2772286.
  38. ^ Хартер, У. Г. (1971). «Усиление скорости в экспериментах по столкновению с супершарами» (PDF). Американский журнал физики. 39 (6): 656–663. Bibcode:1971AmJPh..39..656H. Дои:10.1119/1.1986253.
  39. ^ Нейв, Р. «Двойное падение мяча». Гиперфизика. Получено 2017-01-28.
  40. ^ Законы австралийского футбола 2017 (PDF). AFL. 2017. с. 15. Получено 2018-01-19.
  41. ^ Официальные правила баскетбола 2014 г. Баскетбольное оборудование (PDF). ФИБА. 2014. с. 12.
  42. ^ Правила игры: 2014–2015 гг. (PDF). ФИФА. 2014. с. 15.
  43. ^ Официальные правила волейбола: 2017–2020 гг. (PDF). ФИВБ. 2016. с. 16.
  44. ^ Официальные правила пляжного волейбола: 2017–2020 (PDF). ФИВБ. 2017. с. 15.
  45. ^ Теннисные мячи, классифицированные поверхности и признанные корты, одобренные ITF (PDF). ITF. 2016. С. 4–5.
  46. ^ Справочник Международной федерации настольного тенниса (PDF). ITTF. 2017. с. 24. Архивировано из оригинал (PDF) на 2018-04-24. Получено 2017-10-20.
  47. ^ Официальные правила Национальной баскетбольной ассоциации: 2013–2014 гг. (PDF). НБА. 2013. с. 10.
  48. ^ Официальные правила игры Национальной футбольной лиги (PDF). НФЛ. 2016. с. 3.
  49. ^ Рубинштейн, Л. (11 мая 2002 г.). "Наконец-то добираемся до COR игры". Глобус и почта. Получено 2017-01-27.
  50. ^ Botelho, G .; Кастильо, М. (11 мая 2015 г.). "'Deflategate: «Дисквалификация на 4 игры для Тома Брэди». CNN. Получено 2017-01-27.
  51. ^ Ну, младший, Т. В .; Karp, B.S .; Рейснер, Л. Л. (2015). Отчет о расследовании в отношении футбольных мячей, использованных во время матча чемпионата AFC 18 января 2015 г. (PDF). Paul, Weiss, Rifkind, Wharton & Garrison LLP.
  52. ^ «Эволюция мяча». Бейсбольный дайджест: 67. Июль 1963.
  53. ^ Соуэлл, Т. (2011). «Мертвый мяч против живого мяча». Читатель Томаса Соуэлла. Базовые книги. ISBN 9780465022502.

дальнейшее чтение