WikiDer > Эволюционный алгоритм - Википедия
| Часть серии по |
| Искусственный интеллект |
|---|
Технологии |
Глоссарий |
В вычислительный интеллект (CI), эволюционный алгоритм (EA) это подмножество из эволюционные вычисления,[1] общий популяционный метаэвристический оптимизация алгоритм. Советник использует механизмы, вдохновленные биологическая эволюция, Такие как воспроизведение, мутация, рекомбинация, и отбор. Возможные решения к проблема оптимизации играют роль индивидов в популяции, а фитнес-функция определяет качество решений (см. также функция потерь). Эволюция популяции происходит после повторного применения вышеуказанных операторов.
Эволюционные алгоритмы часто хорошо аппроксимируют решения всех типов проблем, потому что в идеале они не делают никаких предположений относительно лежащих в основе фитнес-ландшафт. Методы эволюционных алгоритмов, применяемые к моделированию биологической эволюции, обычно ограничиваются исследованиями микроэволюционные процессы и модели планирования, основанные на клеточных процессах. В большинстве реальных приложений советников вычислительная сложность является запрещающим фактором.[2] Фактически, эта вычислительная сложность связана с оценкой функции приспособленности. Приближение фитнеса является одним из способов преодоления этой трудности. Однако, казалось бы, простой советник может решать часто сложные задачи;[нужна цитата] следовательно, между сложностью алгоритма и сложностью проблемы может не быть прямой связи.
Выполнение
Ниже приведен пример универсального одноцелевого генетический алгоритм.
Шаг 1. Создайте начальную численность населения из отдельные лица случайно. (Первое поколение)
Шаг второй: повторите следующие шаги восстановления до завершения:
- Оцените фитнес каждого человека в популяции (ограничение по времени, достигнутая достаточная физическая подготовка и т. д.)
- Выберите наиболее подходящих людей для воспроизведение. (Родители)
- Порода новые люди через кроссовер и мутация операции по рождению потомство.
- Замените наименее приспособленных особей населения новыми особями.
Типы
Подобные техники отличаются генетическое представление и другие детали реализации, а также характер конкретной прикладной проблемы.
- Генетический алгоритм - Это самый популярный тип советников. Кто-то ищет решение проблемы в форме цепочек чисел (традиционно двоичных, хотя наилучшими представлениями обычно являются те, которые отражают что-то о решаемой проблеме),[2] применяя такие операторы, как рекомбинация и мутация (иногда один, иногда оба). Этот тип советников часто используется в оптимизация проблемы.
- Генетическое программирование - Здесь решения представлены в виде компьютерных программ, и их пригодность определяется их способностью решать вычислительную задачу.
- Эволюционное программирование - Подобно генетическому программированию, но структура программы фиксирована, а ее числовые параметры могут изменяться.
- Программирование экспрессии генов - Подобно генетическому программированию, GEP также развивает компьютерные программы, но исследует систему генотип-фенотип, где компьютерные программы разных размеров закодированы в линейных хромосомах фиксированной длины.
- Стратегия развития - Работает с векторами действительных чисел в качестве представления решений и обычно использует самоадаптивные скорости мутации.
- Дифференциальная эволюция - Основан на векторных различиях и поэтому в первую очередь подходит для численная оптимизация проблемы.
- Нейроэволюция - Подобно генетическому программированию, но геномы представляют собой искусственные нейронные сети, описывая структуру и веса связей. Кодирование генома может быть прямым или косвенным.
- Система обучающих классификаторов - Здесь решение - это набор классификаторов (правил или условий). Michigan-LCS развивается на уровне отдельных классификаторов, тогда как Pittsburgh-LCS использует совокупности наборов классификаторов. Первоначально классификаторы были только бинарными, но теперь они включают реальные, нейронные сети или S-выражение типы. Пригодность обычно определяется на основе силы или точности. обучение с подкреплением или же контролируемое обучение подход.
Сравнение с биологическими процессами
Возможное ограничение[согласно кому?] многих эволюционных алгоритмов - это отсутствие четкого генотип-фенотип различие. В природе оплодотворенная яйцеклетка подвергается сложному процессу, известному как эмбриогенез стать зрелым фенотип. Это косвенное кодирование считается, что делает генетический поиск более надежным (т.е. снижает вероятность фатальных мутаций), а также может улучшить эволюционируемость организма.[3][4] Такие косвенные (также известные как генеративные или развивающиеся) кодирования также позволяют эволюции использовать закономерность окружающей среды.[5] Последние работы в области искусственный эмбриогенез, или искусственные системы развития, стремится решить эти проблемы. И программирование экспрессии генов успешно исследует систему генотип-фенотип, где генотип состоит из линейных мультигенных хромосом фиксированной длины, а фенотип состоит из нескольких деревьев экспрессии или компьютерных программ разных размеров и форм.[6][неправильный синтез?]
Связанные методы
Алгоритмы роя[требуется разъяснение] включают
- Оптимизация колонии муравьев - Основан на идеях, связанных с поиском пищи муравьями с помощью феромонной коммуникации для формирования путей. В первую очередь подходит для комбинаторная оптимизация и график проблемы.
- Алгоритм «бегун-корень» (RRA) основан на функции побегов и корней растений в природе.[7]
- Алгоритм искусственной пчелиной семьи - На основе поведения медоносных пчел при кормлении. В первую очередь предлагается для численной оптимизации и расширен для решения задач комбинаторной, ограниченной и многокритериальной оптимизации.
- Алгоритм пчел основан на кормлении медоносных пчел. Он применялся во многих приложениях, таких как маршрутизация и планирование.
- Кукушка поиск вдохновлен задумчивым паразитизмом кукушка разновидность. Он также использует Леви рейсы, поэтому он подходит для глобальных оптимизация проблемы.
- Оптимизация Electimize - основана на поведении потока электронов через ветви электрической цепи с наименьшим электрическим сопротивлением.[8]
- Оптимизация роя частиц - На основе представлений о стайном поведении животных. Также в первую очередь подходит для численная оптимизация проблемы.
Другое по населению метаэвристический методы
- Охота Поиск - Метод, вдохновленный групповой охотой на некоторых животных, таких как волки, которые организуют свое положение так, чтобы окружать добычу, каждое из них относительно положения других, и особенно положения их лидера. Это метод непрерывной оптимизации[9] адаптирован как метод комбинаторной оптимизации.[10]
- Адаптивный размерный поиск - В отличие от метаэвристических методов, вдохновленных природой, алгоритм адаптивного размерного поиска не реализует никаких метафор в качестве основного принципа. Скорее, он использует простой ориентированный на производительность метод, основанный на обновлении параметра отношения размерности поиска (SDR) на каждой итерации.[11]
- Алгоритм светлячка навеян поведением светлячков, привлекающих друг друга мигающим светом. Это особенно полезно для мультимодальной оптимизации.
- Поиск гармонии - На основе представлений о поведении музыкантов в поисках лучших гармоний. Этот алгоритм подходит как для комбинаторной оптимизации, так и для оптимизации параметров.
- Гауссовская адаптация - На основе теории информации. Используется для максимизации выхода продукции, средний фитнес или же средняя информация. См. Например Энтропия в термодинамике и теории информации.
- Меметический алгоритм - Гибридный метод, вдохновленный Ричард ДокинзВ понимании мемов он обычно принимает форму алгоритма, основанного на популяциях, в сочетании с индивидуальными процедурами обучения, способными выполнять локальные уточнения. Подчеркивает использование специфических для проблемы знаний и пытается согласовать локальный и глобальный поиск синергетическим образом.
Примеры
В 2020 г. Google заявили, что их AutoML-Zero может успешно заново открыть для себя классические алгоритмы, такие как концепция нейронных сетей.[12]
Компьютерное моделирование Тьерра и Вида попытаться смоделировать макроэволюционный динамика.
Галерея
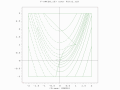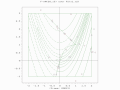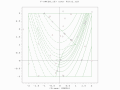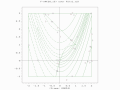
Двухпопуляционный поиск EA по ограниченному Функция Розенброка с ограниченным глобальным оптимумом.
Двухпопуляционный поиск EA по ограниченному Функция Розенброка. Глобальный оптимум не ограничен.
Двухпопуляционный поиск ограниченного оптимума Функция Симионеску.
Рекомендации
- ^ Вихарь П.А. (2016). «Эволюционные алгоритмы: критический обзор и его перспективы на будущее». Труды Международной конференции по глобальным тенденциям в обработке сигналов, информационных вычислениях и коммуникации 2016 г. (ICGTSPICC). Джалгаон: 261–265. Дои:10.1109 / ICGTSPICC.2016.7955308. ISBN 978-1-5090-0467-6. S2CID 22100336.
- ^ а б Кохун, Дж; и другие. (2002-11-26). Эволюционные алгоритмы физического проектирования схем СБИС (PDF). Достижения в эволюционных вычислениях: теория и приложения. Springer, стр. 683-712, 2003. ISBN 978-3-540-43330-9.
- ^ Г.С. Хорнби и Дж. Б. Поллак. «Создание компонентов высокого уровня с генеративным представлением для эволюции тела и мозга». Искусственная жизнь, 8(3):223–246, 2002.
- ^ Джефф Клун, Бенджамин Бекманн, Чарльз Офриа и Роберт Пеннок. «Развитие скоординированных походок четвероногих с помощью генеративного кодирования HyperNEAT» В архиве 2016-06-03 в Wayback Machine. Материалы специальной секции Конгресса IEEE по эволюционным вычислениям по эволюционной робототехнике, 2009. Тронхейм, Норвегия.
- ^ Дж. Клун, К. Офрия и Р. Т. Пеннок, «Как генеративное кодирование работает по мере уменьшения регулярности проблемы», в PPSN (Г. Рудольф, Т. Янсен, С. М. Лукас, К. Полони и Н. Бойме, ред.), Т. 5199 из Конспект лекций по информатике, стр. 358–367, Springer, 2008.
- ^ Феррейра, К., 2001. «Программирование экспрессии генов: новый адаптивный алгоритм решения проблем». Сложные системы, Vol. 13, выпуск 2: 87–129.
- ^ Ф. Меррих-Баят, «Алгоритм« бегунок-корень »: метаэвристика для решения задач одномодальной и мультимодальной оптимизации, вдохновленная побегами и корнями растений в природе» Прикладные мягкие вычисления, Vol. 33. С. 292–303, 2015.
- ^ Халафаллах Ахмед; Абдель-Рахим Мохамед (01.05.2011). «Electimize: новый эволюционный алгоритм оптимизации с применением в строительстве». Журнал вычислительной техники в гражданском строительстве. 25 (3): 192–201. Дои:10.1061 / (ASCE) CP.1943-5487.0000080.
- ^ Oftadeh, R .; Mahjoob, M.J .; Шариатпанахи, М. (октябрь 2010 г.). «Новый алгоритм метаэвристической оптимизации, вдохновленный групповой охотой на животных: поиск по охоте». Компьютеры и математика с приложениями. 60 (7): 2087–2098. Дои:10.1016 / j.camwa.2010.07.049.
- ^ Амин Агаргор; Мохаммед Эссаид Риффи (2017). "Первая адаптация алгоритма поиска охоты для задачи квадратичного назначения". Успехи сотрудничества Европы и Ближнего Востока и Северной Африки в области информационных и коммуникационных технологий. Достижения в интеллектуальных системах и вычислениях. 520: 263–267. Дои:10.1007/978-3-319-46568-5_27. ISBN 978-3-319-46567-8.
- ^ Хасанчеби, О., Каземзаде Азад, С. (2015), «Адаптивный размерный поиск: новый метаэвристический алгоритм для оптимизации размеров дискретной фермы», Компьютеры и конструкции, 154, 1–16.
- ^ Гент, Эдд (13 апреля 2020 г.). «Искусственный интеллект развивается сам по себе». Наука | AAAS. Архивировано из оригинал 16 апреля 2020 г.. Получено 16 апреля 2020.
- ^ Simionescu, P.A .; Beale, D.G .; Дозье, Г. (2004). «Решение задач ограниченной оптимизации с использованием алгоритмов оценки распределения» (PDF). Proc. Конгресса 2004 г. по эволюционным вычислениям - CEC2004. Портленд, штат Орегон: 1647–1653. Дои:10.1109 / CEC.2006.1688506. S2CID 1717817. Получено 7 января 2017. Цитировать журнал требует
| журнал =(помощь) - ^ Simionescu, P.A .; Dozier, G.V .; Уэйнрайт, Р.Л. (2006). «Эволюционный алгоритм для двух популяций для задач оптимизации с ограничениями» (PDF). 2006 Международная конференция IEEE по эволюционным вычислениям. Proc 2006 Международная конференция IEEE по эволюционным вычислениям. Ванкувер, Канада. С. 1647–1653. Дои:10.1109 / CEC.2006.1688506. ISBN 0-7803-9487-9. S2CID 1717817. Получено 7 января 2017.
- ^ Симионеску, П.А. (2014). Инструменты компьютерного построения графиков и моделирования для пользователей AutoCAD (1-е изд.). Бока-Ратон, Флорида: CRC Press. ISBN 978-1-4822-5290-3.
внешняя ссылка
Библиография
- Эшлок, Д. (2006), Эволюционные вычисления для моделирования и оптимизации, Спрингер, ISBN 0-387-22196-4.
- Бэк, Т. (1996), Эволюционные алгоритмы в теории и практике: стратегии эволюции, эволюционное программирование, генетические алгоритмы, Oxford Univ. Нажмите.
- Бэк, Т., Фогель, Д., Михалевич, З. (1997), Справочник по эволюционным вычислениям, Oxford Univ. Нажмите.
- Банцаф, В., Нордин, П., Келлер, Р., Франсоне, Ф. (1998), Генетическое программирование - введение, Морган Кауфманн, Сан-Франциско
- Эйбен, A.E., Смит, J.E. (2003), Введение в эволюционные вычисления, Springer.
- Голландия, Дж. Х. (1992), Адаптация в естественных и искусственных системах, Издательство Мичиганского университета, Анн-Арбор
- Михалевич З., Фогель Д. Б. (2004). Как это решить: современная эвристика, Springer.
- Бенко, Аттила; Доса, Дьердь; Туза, Жолт (2010). «Упаковка / закрытие бункеров с доставкой, решенная эволюцией алгоритмов». 2010 Пятая международная конференция IEEE по биоинженерным вычислениям: теории и приложения (BIC-TA). С. 298–302. Дои:10.1109 / BICTA.2010.5645312. ISBN 978-1-4244-6437-1. S2CID 16875144.
- Poli, R .; Langdon, W. B .; Макфи, Н. Ф. (2008). Полевое руководство по генетическому программированию. Lulu.com, свободно доступный в Интернете. ISBN 978-1-4092-0073-4. Архивировано из оригинал на 2016-05-27. Получено 2011-03-05.[самостоятельно опубликованный источник]
- Прайс К., Сторн Р.М., Лампинен Дж. А. (2005). «Дифференциальная эволюция: практический подход к глобальной оптимизации», Springer.
- Инго Рехенберг (1971): Evolutionsstrategie - Optimierung technischer Systeme nach Prinzipien der biologischen Evolution (кандидатская диссертация). Перепечатано Фромман-Хольцбугом (1973).
- Ханс-Пауль Швефель (1974): Numerische Optimierung von Computer-Modellen (докторская диссертация). Перепечатано Биркхойзером (1977).
- Саймон, Д. (2013): Алгоритмы эволюционной оптимизации, Wiley.
- Вычислительный интеллект: методологическое введение Авторы: Kruse, Borgelt, Klawonn, Moewes, Steinbrecher, Held, 2013, Springer, ISBN 978-1-4471-5012-1
- Rahman, Rosshairy Abd .; Кендалл, Грэм; Рамли, Разамин; Джамари, Зайноддин; Ку-Махамуд, Ку Рухана (2017). «Составление корма для креветок с помощью эволюционного алгоритма с эвристикой мощности для преодоления ограничений». Сложность. 2017: 1–12. Дои:10.1155/2017/7053710.