WikiDer > Правило конечного деления

Перспективная проекция додекаэдрическая мозаика в ЧАС³. Обратите внимание на рекурсивную структуру: каждый пятиугольник содержит меньшие пятиугольники, которые содержат меньшие пятиугольники. Это пример правила подразделения, возникающего из конечной вселенной (т.е. закрыто 3-х коллекторный).

В математике правило конечного подразделения рекурсивный способ деления многоугольник или другую двумерную форму на все меньшие и меньшие части. Правила подразделения в некотором смысле являются обобщениями регулярных геометрических фракталы. Вместо того, чтобы повторять один и тот же дизайн снова и снова, они имеют небольшие вариации на каждом этапе, что позволяет получить более богатую структуру, сохраняя при этом элегантный стиль фракталов.^[1] Правила подразделения использовались в архитектуре, биологии и информатике, а также при изучении гиперболические многообразия. Замещающие мозаики являются хорошо изученным типом правила подразделения.

Определение

Правило подразделения требует черепица плоскости полигонами и превращает ее в новую мозаику, разбиваякаждый многоугольник на более мелкие многоугольники. это конечный если есть только конечное число способов, которыми каждый многоугольник может подразделить. Каждый способ разделения плитки называется тип плитки. Каждый тип плитки представлен меткой (обычно буквой). Каждый тип плитки подразделяется на более мелкие типы плитки. Каждое ребро также подразделяется на конечное число типы кромок. Правила конечного подразделения могут разделять только плитки, состоящие из многоугольников, помеченных типами плиток. Такие мозаики называются подразделения комплексов для правила подразделения. Учитывая любой комплекс подразделов для правила подразделения, мы можем подразделить его снова и снова, чтобы получить последовательность мозаик.

Например, двоичное подразделение имеет один тип плитки и один тип кромки:

Поскольку единственный тип плитки - четырехугольник, двоичное подразделение может только разбивать мозаику, состоящую из четырехугольника. Это означает, что единственные комплексы деления - это мозаики четырехугольниками. Плитка может быть обычный, но не обязательно:

Здесь мы начнем с комплекса, состоящего из четырех четырехугольников, и разделим его дважды. Все четырехугольники представляют собой плитки типа А.

Примеры правил конечного подразделения

Барицентрическое подразделение является примером правила подразделения с одним типом ребра (который подразделяется на два ребра) и одним типом плитки (треугольник, который подразделяется на 6 меньших треугольников). Любая триангулированная поверхность представляет собой комплекс барицентрических подразделений.^[1]

В Плитка Пенроуза могут быть сгенерированы правилом подразделения для набора из четырех типов плиток (изогнутые линии в таблице ниже только помогают показать, как плитки сочетаются друг с другом):

Имя	Начальные плитки	Поколение 1	Поколение 2	Поколение 3
Полукайт
Полудроток
солнце
Звезда

Определенный рациональные карты порождают правила конечного подразделения.^[2] Сюда входит большинство Карты Латте.^[3]

Каждый простой, неразделенный чередующий узел или дополнение звена имеет правило подразделения с некоторыми тайлами, которые не разделяются, что соответствует границе дополнения ссылки.^[4] Правила деления показывают, как будет выглядеть ночное небо для человека, живущего в узел дополнения; потому что Вселенная вращается вокруг себя (т.е. односвязный), наблюдатель увидел бы, как видимая Вселенная повторяется в бесконечном порядке. Правило подразделения описывает этот образец.

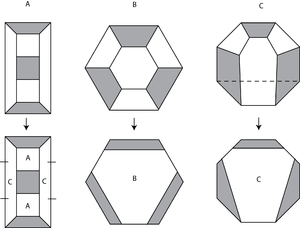
Правило подразделения выглядит по-разному для разной геометрии. Это правило подразделения для трилистник, что не является гиперболический узел:

И это правило подразделения для Кольца Борромео, что является гиперболическим:

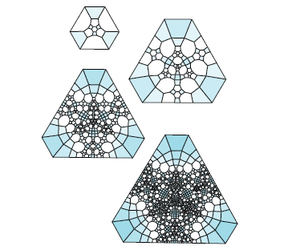
В каждом случае правило подразделения будет действовать на некоторый фрагмент сферы (то есть ночное небо), но проще нарисовать небольшую часть ночного неба, соответствующую одному фрагменту, который многократно разбивается на части. Вот что происходит с узлом-трилистником:

А для колец Борромео:

Правила подразделения в высших измерениях

Правила подразделения можно легко обобщить на другие измерения.^[5] Например, барицентрическое подразделение используется во всех измерениях. Кроме того, двоичное подразделение может быть обобщено на другие измерения (где гиперкубы делятся на каждую промежуточную плоскость), как в доказательстве Теорема Гейне – Бореля.

Строгое определение

Правило деления четырехмерного тора. Грани плиток B, которые подразделяются, могут касаться только плиток C, а грани плиток B, которые касаются не только плиток A.

А правило конечного подразделения ${ displaystyle R}$ состоит из следующего.^[1]

1. Конечная двумерная CW комплекс ${ displaystyle S_ {R}}$, называется дивизионный комплекс, с фиксированной структурой ячеек такой, что ${ displaystyle S_ {R}}$ является объединением его замкнутых 2-клеток. Считаем, что для каждой замкнутой 2-ячейки ${ displaystyle { tilde {s}}}$ из ${ displaystyle S_ {R}}$ есть структура CW ${ displaystyle s}$ на замкнутом 2-диске такой, что ${ displaystyle s}$ имеет не менее двух вершин, вершин и ребер ${ displaystyle s}$ содержатся в ${ displaystyle partial s}$, а характеристическая карта ${ displaystyle psi _ {s}: s rightarrow S_ {R}}$ который отображается на ${ displaystyle { tilde {s}}}$ ограничивается гомеоморфизмом на каждую открытую клетку.

2. Конечный двумерный комплекс непрерывных волн. ${ Displaystyle R (S_ {R})}$, который является подразделением ${ displaystyle S_ {R}}$.

3. непрерывная сотовая карта ${ Displaystyle phi _ {R}: R (S_ {R}) rightarrow S_ {R}}$ называется карта подразделения, ограничение которого на каждую открытую клетку является гомеоморфизмом на открытую клетку.

Каждый комплекс CW ${ displaystyle s}$ в приведенном выше определении (с заданным характеристическим отображением ${ displaystyle psi _ {s}}$) называется тип плитки.

An ${ displaystyle R}$-комплекс для правила подразделения ${ displaystyle R}$ представляет собой двумерный непрерывный комплекс ${ displaystyle X}$ который является объединением его замкнутых 2-клеток вместе с непрерывным клеточным отображением ${ displaystyle f: X rightarrow S_ {R}}$ ограничение которого на каждую открытую клетку является гомеоморфизмом. Мы можем подразделить ${ displaystyle X}$ в комплекс ${ Displaystyle R (X)}$ требуя, чтобы индуцированное отображение ${ Displaystyle f: R (X) rightarrow R (S_ {R})}$ ограничивается гомеоморфизмом на каждую открытую клетку. ${ Displaystyle R (X)}$ снова ${ displaystyle R}$-комплекс с картой ${ Displaystyle phi _ {R} circ f: R (X) rightarrow S_ {R}}$. Повторяя этот процесс, мы получаем последовательность разделенных ${ displaystyle R}$-комплексы ${ Displaystyle R ^ {п} (X)}$ с картами ${ displaystyle phi _ {R} ^ {n} circ f: R ^ {n} (X) rightarrow S_ {R}}$.

Бинарное подразделение является одним из примеров:^[6]

Комплексное подразделение может быть создано путем склеивания противоположных краев квадрата, что делает его сложным. ${ displaystyle S_ {R}}$ в тор. Карта подразделения ${ displaystyle phi}$ - это карта удвоения на торе, дважды оборачивающая меридиан вокруг себя, а долготу - дважды. Это четырехкратный карта покрытия. Плоскость, выложенная квадратами, является комплексом деления для этого правила деления со структурной картой ${ displaystyle f: mathbb {R} ^ {2} rightarrow R (S_ {R})}$ дается стандартной картой покрытия. При разбиении каждый квадрат на плоскости разбивается на квадраты размером в одну четверть.

Квазиизометрические свойства

График истории средние трети правило подразделения.

Правила подразделения можно использовать для изучения квазиизометрия свойства определенных пространств.^[7] Учитывая правило подразделения ${ displaystyle R}$ и подразделение комплекса ${ displaystyle X}$, мы можем построить график называется график истории который записывает действие правила подразделения. График состоит из двойственные графы каждого этапа ${ Displaystyle R ^ {п} (X)}$вместе с краями, соединяющими каждую плитку в ${ Displaystyle R ^ {п} (X)}$ со своими подразделениями в ${ Displaystyle R ^ {п + 1} (Х)}$.

Свойства квазиизометрии графа истории можно изучить с помощью правил подразделения. Например, график истории квазиизометричен относительно гиперболическое пространство именно тогда, когда правило подразделения конформный, как описано в комбинаторная теорема об отображении Римана.^[7]

Приложения

Применение правил подразделения.

Пример правила подразделения, используемого в исламском искусстве, известного как гирих.

Первые три шага Подразделение Catmull-Clark куба с поверхностью подразделения ниже.

Ветвящийся характер бронхи могут быть смоделированы правилами конечного подразделения.

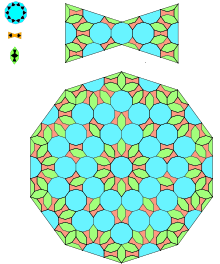
Исламский Гирих плитки в исламской архитектуре - это самоподобные плитки, которые можно смоделировать с помощью правил конечного подразделения.^[8] В 2007, Питер Дж. Лу из Гарвардский университет и профессор Пол Дж. Стейнхардт из Университет Принстона опубликовал статью в журнале Наука предполагая, что гирихские плитки обладают свойствами, соответствующими самоподобный фрактал квазикристаллический плитки, такие как Мозаики Пенроуза (презентация 1974 г., предшествующие работы, начиная примерно с 1964 г.), предшествующие им на пять веков.^[8]

Подразделение поверхностей в компьютерной графике используйте правила подразделения для уточнения поверхности до любого заданного уровня точности. Эти поверхности подразделения (такие как Подразделение поверхности Катмулла-Кларка) взять полигональная сетка (тип, используемый в 3D-анимационных фильмах) и преобразовывает его в сетку с большим количеством полигонов, добавляя и сдвигая точки в соответствии с различными рекурсивными формулами.^[9] Хотя многие точки сдвигаются в этом процессе, каждая новая сетка комбинаторно является подразделением старой сетки (это означает, что для каждого ребра и вершины старой сетки вы можете определить соответствующее ребро и вершину в новой, а также еще несколько ребер. и вершины).

Правила подразделения были применены Кэнноном, Флойдом и Парри (2000) к изучению крупномасштабных моделей роста биологических организмов.^[6] Кэннон, Флойд и Парри создали математическую модель роста, которая продемонстрировала, что некоторые системы, определяемые простыми правилами конечного деления, могут приводить к объектам (в их примере, стволу дерева), крупномасштабная форма которых сильно колеблется со временем, даже если законы местного деления остаются одинаковый.^[6] Кэннон, Флойд и Парри также применили свою модель для анализа структуры роста тканей крыс.^[6] Они предположили, что «отрицательно изогнутая» (или неевклидова) природа микроскопических структур роста биологических организмов является одной из ключевых причин того, почему крупномасштабные организмы не выглядят как кристаллы или многогранные формы, а фактически во многих случаях напоминают самих себя. похожий фракталы.^[6] В частности, они предположили, что такая «отрицательно изогнутая» локальная структура проявляется в сильно сложенном и сильно связанном характере мозга и ткани легких.^[6]

Гипотеза Кэннона

Пушка, Флойд, и Парировать впервые изучил правила конечного подразделения в попытке доказать следующую гипотезу:

Гипотеза Кэннона: Каждый Громов гиперболическая группа с 2-сферой на бесконечности действует геометрически на гиперболическое 3-пространство.^[7]

Здесь геометрическое действие - это кокомпактное, собственно разрывное действие изометрий. Эта гипотеза была частично решена Григорий Перельман в его доказательстве^[10][11][12] из гипотеза геометризации, который утверждает (частично), что любая гиперболическая группа Громова, которая является группой 3-многообразий, должна геометрически действовать на гиперболическом 3-пространстве. Однако остается показать, что гиперболическая группа Громова с 2-сферой на бесконечности является группой 3-многообразий.

Кэннон и Свенсон показали ^[13] что гиперболическая группа с 2-сферой на бесконечности имеет ассоциированное правило подразделения. Если это правило подразделения конформно в определенном смысле, группа будет группой 3-многообразий с геометрией гиперболического 3-пространства.^[7]

Комбинаторная теорема об отображении Римана

Правила подразделения задают последовательность мозаик поверхности, а мозаики дают представление о расстоянии, длине и площади (позволяя каждой плитке иметь длину и площадь 1). В пределе расстояния, которые исходят от этих мозаик, могут в некотором смысле сходиться к аналитическая структура на поверхности. Комбинаторная теорема Римана об отображении дает необходимые и достаточные условия для этого.^[7]

Его заявление требует некоторой предыстории. Плитка ${ displaystyle T}$ кольца ${ displaystyle R}$ (т.е. замкнутое кольцо) дает два инварианта: ${ Displaystyle М _ { sup} (R, T)}$ и ${ Displaystyle м _ { inf} (R, T)}$, называется приблизительные модули. Они похожи на классические модуль кольца. Они определяются использованием весовые функции. Весовая функция ${ displaystyle rho}$ присваивает неотрицательное число, называемое масса к каждой плитке ${ displaystyle T}$. Каждый путь в ${ displaystyle R}$ может быть задана длина, определяемая как сумма весов всех плиток на пути. Определить высота ${ Displaystyle H ( rho)}$ из ${ displaystyle R}$ под ${ displaystyle rho}$ быть точным пределом длины всех возможных путей, соединяющих внутреннюю границу ${ displaystyle R}$ к внешней границе. В длина окружности ${ Displaystyle C ( rho)}$ из ${ displaystyle R}$ под ${ displaystyle rho}$ - это точная нижняя грань длины всех возможных путей, охватывающих кольцо (т.е. не гомотопных нулю в R). В площадь${ Displaystyle А ( rho)}$ из ${ displaystyle R}$ под ${ displaystyle rho}$ определяется как сумма квадратов всех весов в ${ displaystyle R}$. Затем определите

${ Displaystyle M _ { sup} (R, T) = sup { frac {H ( rho) ^ {2}} {A ( rho)}},}$

${ Displaystyle m _ { Inf} (R, T) = Inf { frac {A ( rho)} {C ( rho) ^ {2}}}.}$

Обратите внимание, что они инвариантны относительно масштабирования метрики.

Последовательность ${ displaystyle T_ {1}, T_ {2}, ldots}$ мозаики конформный (${ displaystyle K}$) если сетка приближается к 0 и:

1. Для каждого кольца ${ displaystyle R}$, приближенные модули ${ Displaystyle M _ { sup} (R, T_ {i})}$ и ${ displaystyle m _ { inf} (R, T_ {i})}$, для всех ${ displaystyle i}$ достаточно большие, лежат в единственном интервале вида ${ displaystyle [r, Kr]}$; и
2. Учитывая точку ${ displaystyle x}$ на поверхности, окрестности ${ displaystyle N}$ из ${ displaystyle x}$, и целое число ${ displaystyle I}$, есть кольцо ${ displaystyle R}$ в ${ Displaystyle N smallsetminus {х }}$ разделение Икс из дополнения ${ displaystyle N}$, так что для всех больших ${ displaystyle i}$ приблизительные модули ${ displaystyle R}$ все больше, чем ${ displaystyle I}$.^[7]

Формулировка теоремы

Если последовательность ${ displaystyle T_ {1}, T_ {2}, ldots}$ мозаик поверхности конформно (${ displaystyle K}$) в указанном выше смысле, то существует конформная структура на поверхности и постоянный ${ displaystyle K '}$ в зависимости только от ${ displaystyle K}$ в котором классические модули и приближенные модули (из ${ displaystyle T_ {i}}$ за ${ displaystyle i}$ достаточно большие) любого данного кольца являются ${ displaystyle K '}$-сравненные, что означает, что они лежат в одном интервале ${ displaystyle [r, K'r]}$.^[7]

Последствия

Комбинаторная теорема об отображении Римана влечет, что группа ${ displaystyle G}$ действует геометрически на ${ displaystyle mathbb {H} ^ {3}}$ тогда и только тогда, когда он гиперболический по Громову, у него есть сфера на бесконечности, и правило естественного подразделения на сфере порождает последовательность мозаик, которая является конформной в указанном выше смысле. Таким образом, гипотеза Кэннона была бы верной, если бы все такие правила подразделения были конформными.^[13]

Рекомендации

внешняя ссылка

• Страница исследования Билла Флойда. Эта страница содержит большинство исследовательских работ Кэннона, Флойда и Парри по правилам подразделения, а также галерею правил подразделения.