WikiDer > Изометрическая проекция

Isometric projection
Некоторые 3D-фигуры используют метод изометрического рисования. Черные размеры - это истинные длины, найденные в ортогональной проекции. Красные размеры используются при рисовании методом изометрического рисования. Те же трехмерные фигуры, нарисованные в изометрической проекции, будут казаться меньше; изометрическая проекция покажет стороны объекта в ракурсе примерно на 80%.
Не путать с Изометрия.
Об изометрической проекции в видеоиграх см. изометрическая графика видеоигр.
Часть серии по
Графическая проекция
Аксонометрическая проекция.svg

Изометрическая проекция это метод визуального представления трехмерных объектов в двух измерениях в технический и инженерные чертежи. Это аксонометрическая проекция в котором три оси координат кажутся одинаково укороченными, а угол между любыми двумя из них составляет 120 градусов.

[1]Это живописная орфографическая проекция объекта, в которой прозрачный куб содержащий объект наклоняется перед одним из сплошные диагонали куба становится перпендикулярно вертикальная плоскость вместе с тремя осями одинаково наклонена к этой вертикальной плоскости.

Обзор

Изометрический рисунок куба
Поворот камеры, необходимый для достижения этой перспективы
Классификация Изометрическая проекция и некоторые 3D-проекции

Термин «изометрический» происходит от Греческий для "равной меры", отражая, что масштаб вдоль каждой оси проекции одинаков (в отличие от некоторых других форм графическая проекция).

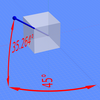
Изометрический вид объекта можно получить, выбрав направление взгляда таким образом, чтобы углы между проекциями Икс, у, и z топоры все одинаковые, или 120 °. Например, с кубом это можно сделать, сначала глядя прямо на одну грань. Затем куб поворачивается на ± 45 ° вокруг вертикальной оси, после чего следует поворот примерно на 35,264 ° (точно arcsin1⁄√3 или арктан1⁄√2, что связано с Магический угол) относительно горизонтальной оси. Обратите внимание, что с кубом (см. Изображение) периметр результирующего 2D-рисунка представляет собой идеальный правильный шестиугольник: все черные линии имеют одинаковую длину, и все грани куба имеют одинаковую площадь. Изометрические миллиметровая бумага может быть помещен под обычную бумагу для рисования, чтобы добиться эффекта без расчетов.

Аналогичным образом изометрический вид можно получить в 3D-сцене. Начиная с камеры, выровненной параллельно полу и выровненной по осям координат, она сначала поворачивается вертикально (вокруг горизонтальной оси) примерно на 35,264 °, как указано выше, а затем на ± 45 ° вокруг вертикальной оси.

Другой способ визуализации изометрической проекции - рассмотрение вида внутри кубической комнаты, начиная с верхнего угла и смотрящего в противоположный, нижний угол. В Икс- ось проходит по диагонали вниз и вправо, у- ось проходит по диагонали вниз и влево, а z- ось прямо вверх. Глубина также показана высотой на изображении. Линии, проведенные по осям, расположены под углом 120 ° друг к другу.

Во всех этих случаях, как и во всех аксонометрический и орфографические проекции, такой камере потребуется объектно-космический телецентрический объектив, чтобы проекционная длина не изменялась с расстоянием от камеры.

Термин «изометрический» часто ошибочно используется для обозначения аксонометрических проекций в целом. Однако на самом деле существует три типа аксонометрических проекций: изометрический, диметрический и триметрический.

Углы поворота

Из двух углов, необходимых для изометрической проекции, значение второго может показаться нелогичным и заслуживает дальнейшего объяснения. Давайте сначала представим куб со сторонами длиной 2, а его центр расположен в начале оси, что означает, что все его грани пересекают оси на расстоянии 1 от начала координат. Мы можем рассчитать длину линии от ее центра до середины любого края как √2 с помощью Теорема Пифагора . Повернув куб на 45 ° на Икс-оси, точка (1, 1, 1) станет (1, 0, √2), как показано на схеме. Второй поворот направлен на то, чтобы поставить ту же точку в положительном свете. z-оси и поэтому необходимо выполнить поворот на значение, равное арктангенс из1⁄√2 что составляет примерно 35,264 °.

Математика

Существует восемь различных ориентаций для получения изометрического вида, в зависимости от того, в какой октант зритель смотрит. Изометрическое преобразование из точки аИкс,у,z в трехмерном пространстве до точки бИкс,у в 2D-пространстве, глядя в первый октант, можно математически записать матрицы вращения в качестве:

где α = arcsin (tan 30 °) ≈ 35,264 ° и β = 45 °. Как объяснялось выше, это вращение вокруг вертикали (здесь у) ось βс последующим вращением вокруг горизонтали (здесь Икс) ось α. Затем следует ортогональная проекция на ху-самолет:

Остальные 7 возможностей получаются путем поворота в противоположные стороны или без, а затем инвертирования направления взгляда или нет.[2]

История и ограничения

Модель оптико-шлифовального двигателя (1822 г.) в изометрии 30 °.[3]
Пример аксонометрического искусства в иллюстрированном издании Романс трех королевств, Китай, гр. 15 век.
Основные статьи: Аксонометрическая проекция и Невозможный объект

Впервые оформлено профессором Уильям Фариш (1759–1837), концепция изометрия в грубой эмпирической форме существовала веками.[4][5] С середины XIX века изометрия стала «бесценным инструментом для инженеров, и вскоре после этого аксонометрия и изометрия были включены в учебную программу курсов архитектурной подготовки в Европе и США».[6] По словам Яна Крикке (2000)[7] однако «аксонометрия возникла в Китай. Его функция в китайском искусстве была похожа на линейная перспектива в европейском искусстве. Аксонометрия и связанная с ней графическая грамматика приобрели новое значение с появлением визуальных вычислений ".[7]

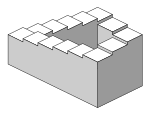
Пример ограничений изометрической проекции. Разницу высот между красными и синими шарами нельзя определить локально.
В Лестница Пенроуза изображает лестницу, которая поднимается (против часовой стрелки) или спускается (по часовой стрелке), но образует непрерывную петлю.

Как и все виды параллельная проекцияобъекты, нарисованные с помощью изометрической проекции, не кажутся больше или меньше по мере приближения к зрителю или от него. Хотя выгодно для архитектурные чертежи там, где измерения необходимо проводить напрямую, результатом является воспринимаемое искажение, в отличие от перспективная проекция, это не как человеческое зрение или фотография нормально работают. Это также может легко привести к ситуациям, когда глубину и высоту трудно измерить, как показано на рисунке справа. Это может показаться парадоксальным или невозможные формы, такой как Лестница Пенроуза.

Использование в видеоиграх и пиксельной графике

Основная статья: Изометрическая компьютерная графика

Изометрическая графика широко использовалась в видеоиграх в течение 1980-х и 1990-х годов, поскольку эта техника обеспечивала ограниченный трехмерный эффект, который мог быть достигнут с ограниченными ресурсами микрокомпьютеры эпохи. Этот стиль также используется для спрайты и пиксельная графика, достигнув характерного стиля, который все еще используется в ретро-игры.

Смотрите также

использованная литература

  1. ^ «Что такое изометрическая проекция | Принцип изометрической проекции | Изометрический масштаб». CivilJungle. 2020-04-25. Получено 2020-10-24.
  2. ^ Ингрид Карлбом; Джозеф Пасиорек; Дэн Лим (декабрь 1978 г.). «Плоские геометрические проекции и трансформации просмотра». Опросы ACM Computing. 10 (4): 465–502. CiteSeerX 10.1.1.532.4774. Дои:10.1145/356744.356750.
  3. ^ Уильям Фэриш (1822) «Об изометрической перспективе». В: Кембриджские философские труды. 1 (1822).
  4. ^ Барклай Дж. Джонс (1986). Защита исторической архитектуры и музейных коллекций от стихийных бедствий. Университет Мичигана. ISBN 0-409-90035-4. стр.243.
  5. ^ Чарльз Эдмунд Мурхаус (1974). Визуальные сообщения: графическая коммуникация для старшеклассников.
  6. ^ Дж. Крикке (1996). "Китайская перспектива киберпространства? В архиве 2016-02-05 в Wayback Machine". В: Информационный бюллетень Международного института азиатских исследований, 9, лето 1996.
  7. ^ а б Ян Крикке (2000). «Аксонометрия: вопрос перспективы». В: Компьютерная графика и приложения, IEEE Июль / август 2000 г. Том 20 (4), стр. 7–11.

внешние ссылки