WikiDer > Эффект Джоуля – Томсона
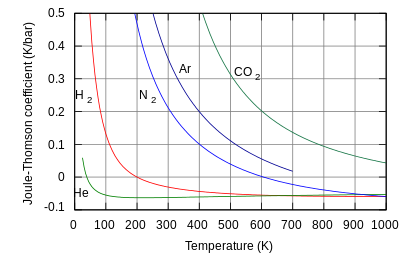
В термодинамика, то Эффект Джоуля – Томсона (также известный как Эффект Джоуля – Кельвина или Эффект Кельвина – Джоуля) описывает изменение температуры настоящий газ или жидкость (в отличие от идеальный газ), когда он проходит через клапан или пористая пробка сохраняя его изолированным, чтобы тепло не передается с окружающей средой.[1][2][3] Эта процедура называется процесс дросселирования или Процесс Джоуля – Томсона.[4] При комнатной температуре все газы, кроме водород, гелий, и неон остывают при расширении по процессу Джоуля – Томсона, когда задушен через отверстие; эти три газа оказывают одинаковый эффект, но только при более низких температурах.[5][6] Большинство жидкостей, таких как гидравлический масла будут нагреваться в процессе дросселирования Джоуля – Томсона.
Процесс дросселирования газового охлаждения обычно используется в холодильные процессы такие как Кондиционеры, тепловые насосы, и ожижители.[7][8] В гидравлике эффект нагрева от дросселирования Джоуля-Томсона может быть использован для обнаружения внутренних утечек в клапанах, поскольку они будут выделять тепло, которое может быть обнаружено термопара или тепловизионная камера. Дросселирование - это принципиально необратимый процесс. Дросселирование из-за сопротивления потоку в линиях подачи, теплообменниках, регенераторах и других компонентах (тепловых) машин является источником потерь, ограничивающих производительность.
История
Эффект назван в честь Джеймс Прескотт Джоуль и Уильям Томсон, первый барон Кельвин, который открыл его в 1852 году. Он последовал за более ранней работой Джоуля по Джоулевое расширение, в котором газ свободно расширяется в вакуум и температура не меняется, если газ идеальный.
Описание
В адиабатический (без теплообмена) расширение газа может быть выполнено несколькими способами. Изменение температуры, которое испытывает газ во время расширения, зависит не только от начального и конечного давления, но также от способа, которым осуществляется расширение.
- Если процесс расширения обратимый, что означает, что газ находится в термодинамическое равновесие во все времена его называют изэнтропический расширение. В этом сценарии газ делает положительный Работа при расширении, и его температура понижается.
- В бесплатное расширение, с другой стороны, газ не работает и не поглощает тепло, поэтому внутренняя энергия сохраняется. Увеличенная таким образом температура идеальный газ останется постоянной, но температура реального газа понижается, за исключением очень высокой температуры.[9]
- Метод расширения, обсуждаемый в этой статье, в котором газ или жидкость под давлением п1 течет в область более низкого давления п2 без значительного изменения кинетической энергии, называется расширением Джоуля – Томсона. Расширение по своей сути необратимо. Во время этого расширения энтальпия остается без изменений (см. доказательство ниже). В отличие от свободного расширения, работа выполняется, вызывая изменение внутренней энергии. Увеличение или уменьшение внутренней энергии определяется тем, выполняется ли работа с жидкостью или с помощью жидкости; что определяется начальным и конечным состояниями расширения и свойствами жидкости.
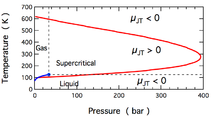
Изменение температуры во время расширения Джоуля – Томсона количественно определяется Коэффициент Джоуля – Томсона, . Этот коэффициент может быть положительным (соответствует охлаждению) или отрицательным (нагрев); области, где каждая встречается для молекулярного азота, N2, показаны на рисунке. Обратите внимание, что большинство условий на рисунке соответствуют N2 будучи сверхкритическая жидкость, где он обладает некоторыми свойствами газа и жидкости, но не может быть описан как таковой. Коэффициент отрицательный как при очень высоких, так и при очень низких температурах; при очень высоком давлении он отрицательный при всех температурах. Максимум температура инверсии (621 K для N2[10]) возникает при приближении к нулевому давлению. Для N2 газ при низких давлениях, отрицательный при высоких температурах и положительный при низких. При температурах ниже газожидкостных кривая сосуществования, N2 конденсируется с образованием жидкости, и коэффициент снова становится отрицательным. Таким образом, для N2 газа ниже 621 К, расширение Джоуля-Томсона может быть использовано для охлаждения газа до тех пор, пока жидкость N2 формы.
Физический механизм
Есть два фактора, которые могут изменить температуру жидкости во время адиабатического расширения: изменение внутренней энергии или преобразование между потенциальной и кинетической внутренней энергией. Температура это мера тепловой кинетической энергии (энергия, связанная с движением молекул); поэтому изменение температуры указывает на изменение тепловой кинетической энергии. В внутренняя энергия представляет собой сумму тепловой кинетической энергии и тепловой потенциальной энергии.[11] Таким образом, даже если внутренняя энергия не изменяется, температура может измениться из-за преобразования кинетической энергии в потенциальную; это то, что происходит при свободном расширении и обычно вызывает снижение температуры по мере расширения жидкости.[12][13] Если работа выполняется с жидкостью или с помощью жидкости по мере ее расширения, общая внутренняя энергия изменяется. Это то, что происходит при расширении Джоуля – Томсона и может вызывать больший нагрев или охлаждение, чем наблюдается при свободном расширении.
В разложении Джоуля – Томсона энтальпия остается постоянной. Энтальпия, , определяется как
где внутренняя энергия, это давление, и объем. В условиях разложения Джоуля – Томсона изменение представляет работу, выполняемую жидкостью (см. доказательство ниже). Если увеличивается, с постоянный, тогда должен уменьшаться в результате работы жидкости с окружающей средой. Это приводит к снижению температуры и положительному коэффициенту Джоуля – Томсона. И наоборот, уменьшение означает, что над жидкостью выполняется работа, и внутренняя энергия увеличивается. Если увеличение кинетической энергии превышает увеличение потенциальной энергии, произойдет повышение температуры жидкости, и коэффициент Джоуля – Томсона будет отрицательным.
Для идеального газа не меняется во время разложения Джоуля – Томсона.[14] В результате внутренняя энергия не изменяется; поскольку также не происходит изменения тепловой потенциальной энергии, не может быть изменений тепловой кинетической энергии и, следовательно, изменения температуры. В реальных газах действительно меняется.
Соотношение стоимости к ожидаемому для идеального газа при той же температуре называется коэффициент сжимаемости, . Для газа это обычно меньше единицы при низкой температуре и больше единицы при высокой температуре (см. Обсуждение в коэффициент сжимаемости). При низком давлении значение всегда движется к единству по мере расширения газа.[15] Таким образом, при низкой температуре, и будет увеличиваться по мере расширения газа, что приводит к положительному коэффициенту Джоуля – Томсона. При высокой температуре, и уменьшаются по мере расширения газа; если уменьшение достаточно велико, коэффициент Джоуля – Томсона будет отрицательным.
Для жидкостей и сверхкритических жидкостей под высоким давлением увеличивается с увеличением давления.[15] Это происходит из-за того, что молекулы прижимаются друг к другу, так что объем едва может уменьшиться из-за более высокого давления. В таких условиях коэффициент Джоуля – Томсона отрицателен, как видно на рисунке. над.
Физический механизм, связанный с эффектом Джоуля-Томсона, тесно связан с механизмом ударная волна,[16] хотя ударная волна отличается тем, что изменением объемной кинетической энергии газового потока нельзя пренебречь.
Коэффициент Джоуля – Томсона (Кельвина)
Скорость изменения температуры по отношению к давлению в процессе Джоуля – Томсона (т. е. при постоянной энтальпии ) это Коэффициент Джоуля – Томсона (Кельвина) . Этот коэффициент можно выразить через объем газа , его теплоемкость при постоянном давлении , и это коэффициент температурного расширения так как:[1][3][17]
Увидеть Вывод коэффициента Джоуля – Томсона. ниже для доказательства этого соотношения. Значение обычно выражается в ° C /бар (Единицы СИ: K/Па) и зависит от типа газа, а также от температуры и давления газа перед расширением. Его зависимость от давления обычно составляет всего несколько процентов для давлений до 100 бар.
Все настоящие газы имеют точка инверсии при котором стоимость меняет знак. Температура этой точки, Температура инверсии Джоуля – Томсона, зависит от давления газа перед расширением.
При расширении газа давление уменьшается, поэтому знак отрицательно по определению. Имея это в виду, следующая таблица объясняет, когда эффект Джоуля-Томсона охлаждает или нагревает реальный газ:
| Если температура газа | тогда является | поскольку является | таким образом должно быть | так что газ |
|---|---|---|---|---|
| ниже температуры инверсии | положительный | всегда отрицательный | отрицательный | охлаждает |
| выше температуры инверсии | отрицательный | всегда отрицательный | положительный | согревает |
Гелий и водород представляют собой два газа, у которых температуры инверсии Джоуля – Томсона при давлении атмосфера очень низкие (например, около 45 К (-228 ° C) для гелия). Таким образом, гелий и водород нагреваются при расширении с постоянной энтальпией при типичных комнатных температурах. С другой стороны, азот и кислородДва самых распространенных газа в воздухе имеют температуру инверсии 621 К (348 ° C) и 764 K (491 ° C) соответственно: эти газы могут быть охлаждены от комнатной температуры с помощью эффекта Джоуля-Томсона.[1]
Для идеального газа всегда равен нулю: идеальные газы ни теплые, ни холодные при расширении при постоянной энтальпии.
Приложения
На практике эффект Джоуля-Томсона достигается за счет расширения газа через дросселирующее устройство (обычно клапан), которые должны быть очень хорошо изолированы, чтобы предотвратить передачу тепла в газ или от него. Во время расширения из газа не извлекается никакая внешняя работа (газ не должен расширяться через турбина, Например).
Охлаждение, полученное при расширении Джоуля – Томсона, делает его ценным инструментом в охлаждение.[18][19] Эффект применяется в Техника Линде как стандартный процесс в нефтехимическая промышленность, где охлаждающий эффект используется для сжиженные газы, а также во многих криогенный применения (например, для производства жидкого кислорода, азота и аргон). Для сжижения в цикле Линде температура газа должна быть ниже температуры инверсии. По этой причине ожижители с простым циклом Linde, начиная с температуры окружающей среды, нельзя использовать для сжижения гелия, водорода или неон. Однако эффект Джоуля-Томсона можно использовать для сжижения даже гелия при условии, что газообразный гелий сначала охладится ниже его температуры инверсии 40 К.[10]
Доказательство того, что удельная энтальпия остается постоянной
| Викиверситет анализирует это доказательство более подробно |
В термодинамике так называемые «специфические» количества - это количества на единицу массы (кг), которые обозначаются строчными буквами. Так час, ты, и v являются удельная энтальпия, удельная внутренняя энергия и удельный объем (объем на единицу массы или обратная плотность) соответственно. В процессе Джоуля – Томсона удельная энтальпия час остается постоянным.[20] Чтобы доказать это, первым делом необходимо вычислить чистую работу, выполненную, когда масса м газа проходит через пробку. Это количество газа имеет объем V1 = м v1 в районе под давлением п1 (область 1) и объем V2 = м v2 когда в районе под давлением п2 (регион 2). Затем в области 1 выполняется "работа потока". на количество остального газа составляет: W1 = м п1v1. В районе 2 работы проделаны от количество газа в остальном газе: W2 = м п2v2. Итак, общая проделанная работа на масса м газа
Изменение внутренней энергии за вычетом общей проделанной работы на количество газа, по первый закон термодинамики, общее количество тепла, подводимого к количеству газа.
В процессе Джоуля – Томсона газ изолирован, поэтому тепло не поглощается. Это значит, что
где ты1 и ты2 обозначают удельные внутренние энергии газа в областях 1 и 2 соответственно. Используя определение удельной энтальпии h = u + Pv, из приведенного выше уравнения следует, что
где h1 и час2 обозначают удельные энтальпии количества газа в областях 1 и 2 соответственно.
Дросселирование в Т-s диаграмма

Очень удобный способ получить количественное представление о процессе дросселирования - это использовать такие диаграммы, как час-Т диаграммы, час-п диаграммы и др. Обычно используются так называемые Т-s диаграммы. На рисунке 2 показан Т-s диаграмма азота в качестве примера.[21] Различные точки обозначены следующим образом:
- а) Т = 300 К, п = 200 бар, s = 5,16 кДж / (кг · К), час = 430 кДж / кг;
- б) Т = 270 К, п = 1 бар, s = 6,79 кДж / (кг · К), час = 430 кДж / кг;
- в) Т = 133 К, п = 200 бар, s = 3,75 кДж / (кг · К), час = 150 кДж / кг;
- г) Т = 77,2 К, п = 1 бар, s = 4,40 кДж / (кг · К), час = 150 кДж / кг;
- д) Т = 77,2 К, п = 1 бар, s = 2,83 кДж / (кг · К), час = 28 кДж / кг (насыщенная жидкость при 1 бар);
- е) Т = 77,2 К, п = 1 бар, s = 5,41 кДж / (кг · К), час = 230 кДж / кг (насыщенный газ при давлении 1 бар).
Как было показано ранее, дросселирование час постоянный. Например. дросселирование от 200 бар и 300 К (точка a на рис. 2) следует изентальпе (линия постоянной удельной энтальпии) 430 кДж / кг. При давлении 1 бар получается точка b с температурой 270 К. Таким образом, дросселирование с 200 бар до 1 бар дает охлаждение от комнатной температуры до температуры ниже точки замерзания воды. Дросселирование от 200 бар и начальной температуры 133 К (точка c на рис. 2) до 1 бара приводит к точке d, которая находится в двухфазной области азота при температуре 77,2 К. Поскольку энтальпия является значительным параметр энтальпия в d (часd) равна энтальпии в e (часе) умноженное на массовую долю жидкости в d (Иксd) плюс энтальпия в f (часж), умноженное на массовую долю газа в d (1 - Иксd). Так
С числами: 150 = Иксd 28 + (1 − Иксd) 230 так Иксd составляет около 0,40. Это означает, что массовая доля жидкости в газожидкостной смеси на выходе из дроссельной заслонки составляет 40%.
Вывод коэффициента Джоуля – Томсона.
Сложно физически представить себе, какой коэффициент Джоуля – Томсона, , представляет собой. Также современные определения не используйте исходный метод, используемый Джоулем и Томсоном, а вместо этого измерьте другую, тесно связанную величину.[22] Таким образом, полезно вывести отношения между и другие, более удобные для измерения величины, как описано ниже.
Первый шаг в получении этих результатов - это отметить, что коэффициент Джоуля – Томсона включает три переменные: Т, п, и ЧАС. Полезный результат сразу получается при применении циклическое правило; в терминах этих трех переменных это правило можно записать
Каждая из трех частных производных в этом выражении имеет определенное значение. Первый - это , второй - постоянное давление теплоемкость, , определяется
а третий - инверсия изотермический коэффициент Джоуля – Томсона, , определяется
- .
Последнюю величину измерить легче, чем .[23][24] Таким образом, выражение из циклического правила принимает вид
Это уравнение можно использовать для получения коэффициентов Джоуля – Томсона из более легко измеряемого изотермического коэффициента Джоуля – Томсона. Далее он используется для получения математического выражения для коэффициента Джоуля – Томсона с точки зрения объемных свойств жидкости.
Чтобы продолжить, отправной точкой является фундаментальное уравнение термодинамики по энтальпии; это
Теперь "делясь" на dп, при постоянной температуре дает
Частная производная слева - это изотермический коэффициент Джоуля – Томсона, , а то, что справа, можно выразить через коэффициент теплового расширения через Отношение Максвелла. Соответствующее соотношение:
где α это кубический коэффициент температурного расширения. Замена этих двух частных производных дает
Это выражение теперь можно заменить в предыдущем уравнении для чтобы получить:
Это дает выражение для коэффициента Джоуля – Томсона в терминах общеизвестных свойств: теплоемкости, молярного объема и коэффициента теплового расширения. Он показывает, что температура инверсии Джоуля – Томсона, при которой равен нулю, возникает, когда коэффициент теплового расширения равен обратной величине температуры. Поскольку это верно при всех температурах для идеальных газов (см. расширение в газах) коэффициент Джоуля – Томсона идеального газа равен нулю при всех температурах.[25]
Второй закон Джоуля
Легко убедиться, что для идеальный газ определяется подходящими микроскопическими постулатами, которые αT = 1, поэтому изменение температуры такого идеального газа при расширении Джоуля – Томсона равно нулю. Для такого идеального газа этот теоретический результат означает, что:
- Внутренняя энергия фиксированной массы идеального газа зависит только от его температуры (а не от давления или объема).
Это правило было первоначально обнаружено Джоулем экспериментально для реальных газов и известно как Второй закон Джоуля. Более изощренные эксперименты, конечно, обнаружили важные отклонения от него.[26][27][28]
Смотрите также
- Критическая точка (термодинамика)
- Энтальпия и Изентальпический процесс
- Идеальный газ
- Сжижение газов
- MIRI (прибор среднего инфракрасного диапазона), петля J – T используется на одном из инструментов Космический телескоп Джеймса Уэбба
- Холодильное оборудование
- Обратимый процесс (термодинамика)
использованная литература
- ^ а б c Р. Х. Перри и Д. У. Грин (1984). Справочник инженеров-химиков Перри. Макгроу-Хилл. ISBN 978-0-07-049479-4.
- ^ Б. Н. Рой (2002). Основы классической и статистической термодинамики. Джон Вили и сыновья. Bibcode:2002fcst.book ..... N. ISBN 978-0-470-84313-0.
- ^ а б У. К. Эдмистер, Б. И. Ли (1984). Прикладная термодинамика углеводородов. Vol. 1 (2-е изд.). Издательство Gulf Publishing. ISBN 978-0-87201-855-6.
- ^ Ф. Рейф (1965). «Глава 5 - Простые приложения макроскопической термодинамики». Основы статистической и теплофизики. Макгроу-Хилл. ISBN 978-0-07-051800-1.
- ^ А. В. Адамсон (1973). «Глава 4 - Химическая термодинамика. Первый закон термодинамики». Учебник физической химии (1-е изд.). Академическая пресса. LCCN 72088328.
- ^ Г. В. Кастеллан (1971). «Глава 7 - Энергия и первый закон термодинамики; термохимия». Физическая химия (2-е изд.). Эддисон-Уэсли. ISBN 978-0-201-00912-5.
- ^ Moran, M.J .; Шапиро, Х.Н. (2006). Основы инженерной термодинамики (5-е изд.). Джон Вили и сыновья.
- ^ Де Вале, А. Т. А. М. (2017). «Основы сжижения Джоуля – Томсона и JT-охлаждения». Журнал физики низких температур. 186 (5–6): 385–403. Bibcode:2017JLTP..186..385D. Дои:10.1007 / s10909-016-1733-3.
- ^ Гуссар, Жак-Оливье; Руле, Бернар (1993). «Свободное расширение для реальных газов». Американский журнал физики. 61 (9): 845–848. Bibcode:1993AmJPh..61..845G. Дои:10.1119/1.17417.
- ^ а б Аткинс, Питер (1997). Физическая химия (6-е изд.). Нью-Йорк: W.H. Freeman and Co. стр.930. ISBN 978-0-7167-2871-9.
- ^ Рок, П. А. (1983). Химическая термодинамика. Милл-Вэлли, Калифорния: Университетские научные книги. сек. 3-2. ISBN 978-0-935702-12-5.
- ^ Пиппард, А. Б. (1957).«Элементы классической термодинамики», с. 73. Cambridge University Press, Кембридж, Великобритания.
- ^ Табор, Д. (1991). Газы, жидкости и твердые вещества, п. 148. Cambridge University Press, Кембридж, Великобритания. ISBN 0 521 40667 6.
- ^ Клотц, И.М. и Р. М. Розенберг (1991). Химическая термодинамика, п. 83. Бенджамин, Мено-Парк, Калифорния.
- ^ а б Аткинс, Питер (1997). Физическая химия (6-е изд.). Нью-Йорк: W.H. Freeman and Co., стр. 31–32. ISBN 0-7167-2871-0.
- ^ Гувер, Вм. Г.; Гувер, Кэрол Дж .; Трэвис, Карл П. (2014). «Ударно-волновое сжатие и расширение Джоуля – Томсона». Письма с физическими проверками. 112 (14): 144504. arXiv:1311.1717. Bibcode:2014ПхРвЛ.112н4504Н. Дои:10.1103 / PhysRevLett.112.144504. PMID 24765974.
- ^ W.R. Salzman. "Джоулевое расширение". Кафедра химии, Университет Аризоны. Архивировано из оригинал 13 июня 2012 г.. Получено 23 июля 2005.
- ^ Де Вале, А. Т. А. М. (2017). «Основы сжижения Джоуля – Томсона и JT-охлаждения». Журнал физики низких температур. 186 (5–6): 385–403. Bibcode:2017JLTP..186..385D. Дои:10.1007 / s10909-016-1733-3.
- ^ Кинан, Дж. (1970). Термодинамика, Глава 15. M.I.T. Press, Кембридж, Массачусетс.
- ^ См. Например М.Дж. Моран и Х.Н. Шапиро «Основы инженерной термодинамики», 5-е издание (2006 г.) John Wiley & Sons, Inc., стр. 147
- ^ Рисунок состоит из данных, полученных с помощью RefProp, стандартной справочной базы данных NIST 23
- ^ Аткинс, Питер (1997). Физическая химия (6-е изд.). Нью-Йорк: W.H. Freeman and Co., стр.89–90. ISBN 978-0-7167-2871-9.
- ^ Keyes, F.G .; Коллинз, С.С. (1932). «Изменение давления тепловой функции как прямая мера сил Ван-дер-Ваальса». Proc. Natl. Акад. Sci. СОЕДИНЕННЫЕ ШТАТЫ АМЕРИКИ. 18 (4): 328–333. Bibcode:1932ПНАС ... 18..328К. Дои:10.1073 / pnas.18.4.328. ЧВК 1076221. PMID 16587688.
- ^ Cusco, L .; McBain, S.E .; Сэвилл, Г. (1995). «Проточный калориметр для измерения изотермического коэффициента Джоуля – Томсона газов при повышенных температурах и давлениях. Результаты для азота при температурах до 473 К и давлениях до 10 МПа и для диоксида углерода при температурах до 500 К и давлениях выше. до 5 МПа ». Журнал химической термодинамики. 27 (7): 721–733. Дои:10.1006 / jcht.1995.0073.
- ^ Каллен, Х. Б. (1960). Термодинамика. Нью-Йорк: Джон Уайли и сыновья. стр.112–114.
- ^ Партингтон, Дж. (1949). Расширенный трактат по физической химии, том 1 Основные принципы. Свойства газов, Longmans, Green and Co., Лондон, стр. 614–615.
- ^ Адкинс, Си-Джей (1968/1983). Равновесная термодинамика, (1-е издание 1968 г.), 3-е издание 1983 г., Cambridge University Press, Cambridge UK, ISBN 0-521-25445-0, п. 116.
- ^ Байлын, М. (1994). Обзор термодинамики, Американский институт физики Press, Нью-Йорк, ISBN 0-88318-797-3, п. 81.
Список используемой литературы
- М. В. Земанский (1968). Тепло и термодинамика; Учебник для среднего уровня. Макгроу-Хилл. стр.182, 355. LCCN 67026891.
- Д. В. Шредер (2000). Введение в теплофизику. Эддисон Уэсли Лонгман. п.142. ISBN 978-0-201-38027-9.
- К. Киттель, Х. Кремер (1980). Теплофизика. В. Х. Фриман. ISBN 978-0-7167-1088-2.
внешние ссылки
| Викискладе есть медиафайлы по теме Эффект Джоуля-Томсона. |
- Вайсштейн, Эрик Вольфганг (ред.). «Процесс Джоуля-Томсона». ScienceWorld.
- Вайсштейн, Эрик Вольфганг (ред.). «Коэффициент Джоуля-Томсона». ScienceWorld.
- «Кривая инверсии эффекта Джоуля-Томсона с использованием CEOS Пенга-Робинсона». Демонстрационные проекты Wolfram Mathematica.
- Модуль эффекта Джоуля – Томсона, Университет Нотр-Дам