WikiDer > Настоящий газ
Настоящие газы являются неидеальными газами, молекулы которых занимают пространство и взаимодействуют друг с другом; следовательно, они не соблюдают закон идеального газа.Чтобы понять поведение реальных газов, необходимо принять во внимание следующее:
- сжимаемость последствия;
- Переменная удельная теплоемкость;
- силы Ван дер Ваальса;
- неравновесные термодинамические эффекты;
- вопросы молекулярной диссоциации и элементарных реакций с переменным составом
Для большинства приложений такой подробный анализ не нужен, и идеальный газ приближение можно использовать с разумной точностью. С другой стороны, модели для реального газа должны использоваться вблизи конденсация точка газов, рядом критические точкипри очень высоких давлениях, чтобы объяснить Эффект Джоуля – Томсона и в других менее обычных случаях. Отклонение от идеальности можно описать коэффициент сжимаемости Z.
Модели

Синие кривые - изотермы ниже критической температуры. Зеленые участки - метастабильные состояния.
Сечение слева от точки F - нормальная жидкость.
Точка F - точка кипения.
Линия FG - равновесие жидкой и газовой фаз.
Раздел FA - перегретая жидкость.
Раздел F′A - растянутая жидкость (р <0).
Раздел AC - аналитическое продолжение изотермы, физически невозможно.
Раздел CG - переохлажденный пар.
Точка G - точка росы.
График справа от точки G - нормальный газ.
Площади FAB и GCB равны.
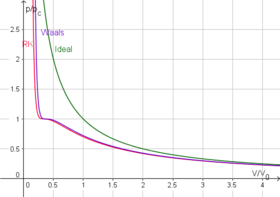
Красная кривая - критическая изотерма.
Точка К - критическая точка.
Голубые кривые - сверхкритические изотермы
Модель Ван дер Ваальса
Реальные газы часто моделируются с учетом их молярной массы и молярного объема.
или альтернативно:
Где п давление, Т это температура, р постоянная идеального газа, и Vм то молярный объем. а и б параметры, которые определяются эмпирически для каждого газа, но иногда оцениваются по их критическая температура (Тc) и критическое давление (пc) используя эти отношения:
Константы в критической точке можно выразить как функции параметров a, b:
С уменьшенные свойства уравнение можно записать в виде уменьшенная форма:
Модель Редлиха – Квонга
В Уравнение Редлиха – Квонга - еще одно двухпараметрическое уравнение, которое используется для моделирования реальных газов. Он почти всегда точнее, чем уравнение Ван-дер-Ваальса, и часто более точным, чем некоторые уравнения с более чем двумя параметрами. Уравнение
или альтернативно:
куда а и б два эмпирических параметра, которые нет те же параметры, что и в уравнении Ван-дер-Ваальса. Эти параметры можно определить:
Константы в критической точке можно выразить как функции параметров a, b:
С помощью уравнение состояния можно записать в виде уменьшенная форма:
- с
Бертло и модифицированная модель Бертло
Уравнение Бертло (названо в честь Д. Бертло)[1] очень редко используется,
но модифицированная версия несколько точнее
Дитеричи модель
Эта модель (названная в честь К. Дитеричи[2]) вышел из употребления в последние годы
с параметрами a, b и
Модель Клаузиуса
Уравнение Клаузиуса (названо в честь Рудольф Клаузиус) представляет собой очень простое трехпараметрическое уравнение, используемое для моделирования газов.
или альтернативно:
куда
куда Vc критический объем.
Вириальная модель
В Вириал уравнение выводится из пертурбативное лечение статистической механики.
или альтернативно
куда А, B, C, А′, B', и C′ - константы, зависящие от температуры.
Модель Пенга – Робинсона
Уравнение состояния Пенга – Робинсона. (названный в честь Д.-Ю. Пэн и Д. Б. Робинсон[3]) обладает интересным свойством, которое можно использовать при моделировании некоторых жидкостей, а также реальных газов.
Модель Wohl
Уравнение Воля (названо в честь А. Воля[4]) сформулирован в терминах критических значений, что делает его полезным, когда реальные газовые константы недоступны, но его нельзя использовать для высоких плотностей, так как, например, критическая изотерма показывает резкое снижаться давления, когда объем сокращается за пределы критического объема.
или же:
или, альтернативно:
куда
- с
- , куда - (соответственно) молярный объем, давление и температура на критическая точка.
И с уменьшенные свойства можно записать первое уравнение в уменьшенная форма:
Модель Битти – Бриджмена
[5] Это уравнение основано на пяти экспериментально определенных константах. Это выражается как
куда
Известно, что это уравнение достаточно точное для плотностей примерно до 0,8.ρcr, куда ρcr - плотность вещества в его критической точке. Константы, фигурирующие в приведенном выше уравнении, доступны в следующей таблице при п в кПа, v в , Т находится в K и р = 8.314[6]
| Газ | А0 | а | B0 | б | c |
|---|---|---|---|---|---|
| Воздуха | 131.8441 | 0.01931 | 0.04611 | −0.001101 | 4.34×104 |
| Аргон, Ar | 130.7802 | 0.02328 | 0.03931 | 0.0 | 5.99×104 |
| Углекислый газ, CO2 | 507.2836 | 0.07132 | 0.10476 | 0.07235 | 6.60×105 |
| Гелий, He | 2.1886 | 0.05984 | 0.01400 | 0.0 | 40 |
| Водород, H2 | 20.0117 | −0.00506 | 0.02096 | −0.04359 | 504 |
| Азот, N2 | 136.2315 | 0.02617 | 0.05046 | −0.00691 | 4.20×104 |
| Кислород, O2 | 151.0857 | 0.02562 | 0.04624 | 0.004208 | 4.80×104 |
Модель Бенедикта – Уэбба – Рубина
Уравнение BWR, иногда называемое уравнением BWRS,
куда d - молярная плотность и где а, б, c, А, B, C, α, и γ являются эмпирическими константами. Обратите внимание, что γ константа является производной константы α и поэтому почти идентичен 1.
Работа по термодинамическому расширению
Работа расширения реального газа отличается от работы идеального газа на величину .
Смотрите также
- Коэффициент сжимаемости
- Уравнение состояния
- Газовые законы
- Закон идеального газа: Закон Бойля и Закон Гей-Люссака
Рекомендации
- ^ Д. Бертело в Travaux et Mémoires du Bureau International des Poids et Mesures - Том XIII (Париж: Готье-Виллар, 1907 г.)
- ^ К. Дитеричи, Анна. Phys. Chem. Wiedemanns Ann. 69, 685 (1899)
- ^ Пэн Д. Ю. и Робинсон Д. Б. (1976). «Новое двухпостоянное уравнение состояния». Промышленная и инженерная химия: основы. 15: 59–64. Дои:10.1021 / i160057a011.
- ^ А. Воль (1914). «Исследование уравнения состояния». Zeitschrift für Physikalische Chemie. 87: 1–39.
- ^ Юнус А. Ценгель и Майкл А. Болес, Термодинамика: инженерный подход 7-е издание, McGraw-Hill, 2010 г., ISBN 007-352932-X
- ^ Гордан Дж. Ван Уилен и Ричард Э. Соннтадж, Основы классической термодинамики, 3-е изд., Нью-Йорк, John Wiley & Sons, 1986 P46, таблица 3.3.
дальнейшее чтение
- Кондепуди, Д. К .; Пригожин И. (1998). Современная термодинамика: от тепловых двигателей до диссипативных структур. Джон Уайли и сыновья. ISBN 978-0-471-97393-5.
- Се, Дж. С. (1993). Инженерная термодинамика. Prentice-Hall. ISBN 978-0-13-275702-7.
- Валас, С. М. (1985). Фазовые равновесия в химической технологии в 2 кастах. Butterworth Publishers. ISBN 978-0-409-95162-2.
- Азнар, М .; Сильва Теллес, А. (1997). «Банк данных параметров для привлекательного коэффициента уравнения состояния Пенга-Робинсона». Бразильский журнал химической инженерии. 14 (1): 19–39. Дои:10.1590 / S0104-66321997000100003.
- Рао, Ю. В. Ц (2004). Введение в термодинамику. Университеты Пресса. ISBN 978-81-7371-461-0.
- Сян, Х. В. (2005). Принцип соответствия состояний и его практика: термодинамические, транспортные и поверхностные свойства жидкостей. Эльзевир. ISBN 978-0-08-045904-2.









![{ displaystyle p_ {c} = { frac {({ sqrt [{3}] {2}} - 1) ^ {7/3}} {3 ^ {1/3}}} R ^ {1 / 3} { frac {a ^ {2/3}} {b ^ {5/3}}}, quad T_ {c} = 3 ^ {2/3} ({ sqrt [{3}] {2 }} - 1) ^ {4/3} ({ frac {a} {bR}}) ^ {2/3}, qquad V_ {m, c} = { frac {b} {{ sqrt [ {3}] {2}} - 1}}, qquad Z_ {c} = { frac {1} {3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2049ffdf2acaa75fec73b555bb8da98d3e4f28b0)


![{ displaystyle b '= { sqrt [{3}] {2}} - 1 приблизительно 0,26}](https://wikimedia.org/api/rest_v1/media/math/render/svg/578b7130159a520fdd079b4a4857ef08fc6e898f)

![{ displaystyle p = { frac {RT} {V _ { text {m}}}} left [1 + { frac {9 { frac {p} {p _ { text {c}}}}} {128 { frac {T} {T _ { text {c}}}}}} left (1 - { frac {6} { frac {T ^ {2}} {T _ { text {c}) } ^ {2}}}} right) right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/104eeedf4bd470d77be66a443ce8dee79018befa)





![{ displaystyle pV _ { text {m}} = RT left [1 + { frac {B (T)} {V _ { text {m}}}}} + { frac {C (T)} {V_ { text {m}} ^ {2}}} + { frac {D (T)} {V _ { text {m}} ^ {3}}} + ldots right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24872e14ac2166d1a8b69843092b4cd5466163c1)
![{ displaystyle pV _ { text {m}} = RT left [1 + B '(T) p + C' (T) p ^ {2} + D '(T) p ^ {3} ldots right ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4210d94e484090005b5c79e62c4d1697b14f79b2)
















![{ displaystyle p = RTd + d ^ {2} left (RT (B + bd) - left (A + ad-a alpha d ^ {4} right) - { frac {1} {T ^ {2}}} left [C-cd left (1+ gamma d ^ {2} right) exp left (- gamma d ^ {2} right) right] right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08d43caaf20d4f8946f7449bba37b3849305619e)
