WikiDer > Закон больших чисел

эта статья нужны дополнительные цитаты для проверка. Пожалуйста помоги улучшить эту статью от добавление цитат в надежные источники. Материал, не полученный от источника, может быть оспорен и удален. Найдите источники: «Закон больших чисел» – Новости · газеты · книги · ученый · JSTOR (Март 2015 г.) (Узнайте, как и когда удалить этот шаблон сообщения)

Иллюстрация закона больших чисел с использованием конкретной серии рулонов одного умри. По мере увеличения количества бросков в этом прогоне среднее значение всех результатов приближается к 3,5. Хотя каждый прогон будет показывать отличительную форму при небольшом количестве бросков (слева), при большом количестве бросков (справа) формы будут очень похожими.

Часть серии по статистика
Теория вероятности
Аксиомы вероятности
Пространство вероятностей Образец пространства Элементарное событие Мероприятие Случайная переменная Вероятностная мера
Дополнительное мероприятие Совместная вероятность Предельная вероятность Условная возможность
Независимость Условная независимость Закон полной вероятности Закон больших чисел Теорема Байеса Неравенство Буля
Диаграмма Венна Древовидная диаграмма
v т е

В теория вероятности, то закон больших чисел (LLN) это теорема который описывает результат выполнения одного и того же эксперимента большое количество раз. Согласно закону, средний результатов, полученных в результате большого количества испытаний, должны быть близки к ожидаемое значение и будет иметь тенденцию приближаться к ожидаемому значению по мере выполнения большего количества испытаний.^[1]

LLN важен, потому что он гарантирует стабильные долгосрочные результаты для средних значений некоторых случайных событий.^[1][2] Например, пока казино может потерять деньги в одном вращении рулетка wheel, его прибыль будет иметь тенденцию к предсказуемому проценту за большое количество вращений. Любая выигрышная серия игрока в конечном итоге будет преодолена параметрами игры. Важно помнить, что закон применяется (как следует из названия) только тогда, когда большое количество наблюдений. Не существует принципа, согласно которому небольшое количество наблюдений будет совпадать с ожидаемым значением или что полоса одного значения будет немедленно «сбалансирована» другими (см. заблуждение игрока).

Примеры

Например, один бросок честных шестигранных кубиков дает одно из чисел 1, 2, 3, 4, 5 или 6, каждое с равным вероятность. Таким образом, ожидаемое значение среднего бросков составляет:

${ displaystyle { frac {1 + 2 + 3 + 4 + 5 + 6} {6}} = 3,5}$

Согласно закону больших чисел, если выпадает большое количество шестигранных игральных костей, среднее из их значений (иногда называемое выборочное среднее), вероятно, будет близко к 3,5, с увеличением точности по мере того, как бросается больше кубиков.

Из закона больших чисел следует, что эмпирическая вероятность успеха в серии Бернулли испытания будет сходиться к теоретической вероятности. Для Случайная величина Бернулли, ожидаемое значение - это теоретическая вероятность успеха, а среднее значение п такие переменные (при условии, что они независимые и одинаково распределенные (i.i.d.)) и есть относительная частота.

Например, честная монета бросок - это испытание Бернулли. Когда честная монета подбрасывается один раз, теоретическая вероятность того, что выпадет орел, равна¹⁄₂. Следовательно, согласно закону больших чисел, доля орлов в «большом» количестве подбрасываний монеты »должна быть« примерно¹⁄₂. В частности, доля голов после п сальто будет почти наверняка сходиться к¹⁄₂ так как п приближается к бесконечности.

Хотя доля орлов (и решек) приближается к 1/2, почти наверняка абсолютная разница количество орлов и решек станет большим по мере того, как станет большим количеством флипов. То есть вероятность того, что абсолютная разница является малым числом, приближается к нулю, когда количество переворотов становится большим. Кроме того, почти наверняка отношение абсолютной разницы к количеству флипов приблизится к нулю. Интуитивно ожидаемая разница растет, но медленнее, чем количество переворотов.

Еще один хороший пример LLN - это Метод Монте-Карло. Эти методы представляют собой широкий класс вычислительный алгоритмы которые полагаются на повторяющиеся случайная выборка для получения численных результатов. Чем больше количество повторений, тем лучше приближение. Причина, по которой этот метод важен, в основном состоит в том, что иногда трудно или невозможно использовать другие подходы.^[3]

Ограничение

Среднее значение результатов, полученных в результате большого количества испытаний, в некоторых случаях может не совпадать. Например, среднее значение п результаты взяты из Распределение Коши или несколько Распределения Парето (α <1) не будет сходиться при п становится больше; причина в том тяжелые хвосты. Распределение Коши и распределение Парето представляют два случая: распределение Коши не имеет математического ожидания,^[4] тогда как математическое ожидание распределения Парето (α <1) бесконечно.^[5] Другой пример: случайные числа равны касательная угла, равномерно распределенного между -90 ° и + 90 °. В медиана равно нулю, но ожидаемого значения не существует, и действительно, среднее значение п такие переменные имеют то же распределение, что и одна такая переменная. Он не сходится по вероятности к нулю (или любому другому значению) как п уходит в бесконечность.

История

Распространение является примером закона больших чисел. Изначально есть растворенное вещество молекулы слева от барьера (пурпурная линия) и ни одного справа. Барьер удаляется, и растворенное вещество диффундирует, заполняя весь контейнер.
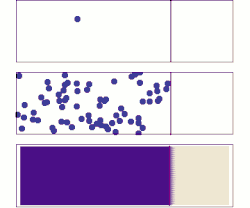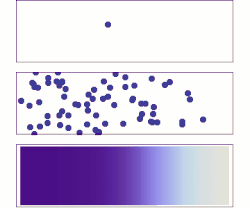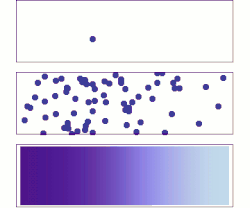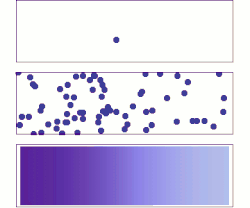
Верхний: В случае одиночной молекулы движение кажется довольно случайным.
Средний: При большем количестве молекул явно наблюдается тенденция к тому, что растворенное вещество заполняет контейнер все более и более равномерно, но также наблюдаются случайные колебания.
Дно: С огромным количеством молекул растворенного вещества (слишком много, чтобы увидеть) случайность по существу исчезла: растворенное вещество, кажется, плавно и систематически перемещается из областей с высокой концентрацией в области с низкой концентрацией. В реальных ситуациях химики могут описать диффузию как детерминированное макроскопическое явление (см. Законы Фика), несмотря на его случайную природу.

Итальянский математик Джероламо Кардано (1501–1576) без доказательств заявили, что точность эмпирической статистики имеет тенденцию улучшаться с увеличением количества испытаний.^[6] Затем это было формализовано как закон больших чисел. Специальная форма LLN (для двоичной случайной величины) была впервые доказана Джейкоб Бернулли.^[7] Ему потребовалось более 20 лет, чтобы разработать достаточно строгое математическое доказательство, которое было опубликовано в его Ars Conjectandi (Искусство гадания) в 1713 году. Он назвал это своей «Золотой теоремой», но она стала широко известна как «Теорема Бернулли". Это не следует путать с Принцип Бернулли, названный в честь племянника Якоба Бернулли Даниэль Бернулли. В 1837 г. S.D. Пуассон далее описал его под названием "La Loi des Grands Nombres"(" закон больших чисел ").^[8][9] В дальнейшем он был известен под обоими названиями, но наиболее часто использовался «закон больших чисел».

После того, как Бернулли и Пуассон опубликовали свои исследования, другие математики также внесли свой вклад в уточнение закона, в том числе Чебышев,^[10] Марков, Борель, Кантелли и Колмогоров и Хинчин. Марков показал, что этот закон может применяться к случайной величине, которая не имеет конечной дисперсии при другом более слабом предположении, а Хинчин показал в 1929 году, что если ряд состоит из независимых одинаково распределенных случайных величин, достаточно, чтобы ожидаемое значение существует для выполнения слабого закона больших чисел.^[11][12] Эти дальнейшие исследования привели к появлению двух известных форм LLN. Один называется «слабым» законом, а другой - «сильным» законом в отношении двух различных способов конвергенция совокупных выборочных средних до ожидаемого значения; в частности, как объясняется ниже, сильная форма подразумевает слабую.^[11]

Формы

Есть две разные версии закон больших чисел которые описаны ниже. Их называют строгий закон большого количества и слабый закон большого количества.^[13][1] Заявлено для случая, когда Икс₁, Икс₂, ... бесконечная последовательность независимые и одинаково распределенные (i.i.d.) Интегрируемые по Лебегу случайные величины с математическим ожиданием E (Икс₁) = E (Икс₂) = ...= µ, обе версии закона заявляют, что - с виртуальной достоверностью - выборочное среднее

${ displaystyle { overline {X}} _ {n} = { frac {1} {n}} (X_ {1} + cdots + X_ {n})}$

сходится к ожидаемому значению

${ displaystyle { begin {matrix} {} { overline {X}} _ {n} , to , mu qquad { textrm {for}} qquad n to infty, {} end {matrix}}}$

(закон. 1)

(Интегрируемость по Лебегу Икс_j означает, что ожидаемое значение E (Икс_j) существует согласно Интеграция Лебега и конечно. Оно делает не означают, что соответствующая вероятностная мера абсолютно непрерывный относительно Мера Лебега.)

Исходя из предположения конечности отклонение ${ displaystyle operatorname {Var} (X_ {i}) = sigma ^ {2}}$ (для всех ${ displaystyle i}$) и отсутствие корреляции между случайными величинами, дисперсия среднего n случайных величин

${ displaystyle operatorname {Var} ({ overline {X}} _ {n}) = operatorname {Var} ({ tfrac {1} {n}} (X_ {1} + cdots + X_ {n })) = { frac {1} {n ^ {2}}} operatorname {Var} (X_ {1} + cdots + X_ {n}) = { frac {n sigma ^ {2}} {n ^ {2}}} = { frac { sigma ^ {2}} {n}}.}$

Иногда предположение о конечном отклонение ${ displaystyle operatorname {Var} (X_ {1}) = operatorname {Var} (X_ {2}) = ldots = sigma ^ {2} < infty}$ является не обязательно. Большая или бесконечная дисперсия замедлит сходимость, но LLN все равно сохраняется. Это предположение часто используется, потому что оно упрощает и сокращает доказательства.

Взаимная независимость случайных величин можно заменить на попарная независимость в обеих версиях закона.^[14]

Разница между сильной и слабой версиями связана с утверждаемым способом конвергенции. Для интерпретации этих режимов см. Сходимость случайных величин.

Слабый закон

Моделирование, иллюстрирующее закон больших чисел. В каждом кадре монета, красная с одной стороны и синяя с другой, переворачивается, и в соответствующий столбец добавляется точка. Круговая диаграмма показывает соотношение красного и синего на данный момент. Обратите внимание, что, хотя сначала пропорция значительно варьируется, по мере увеличения количества испытаний она приближается к 50%.

В слабый закон больших чисел (также называется Хинчинзакон) гласит, что выборочное среднее сходится по вероятности к ожидаемой стоимости^[15]

${ displaystyle { begin {matrix} {} { overline {X}} _ {n} { xrightarrow {P}} mu qquad { textrm {when}} n to infty . {} end {matrix}}}$

(закон. 2)

То есть для любого положительного числа ε,

${ displaystyle lim _ {n to infty} Pr ! left (, | { overline {X}} _ {n} - mu |> varepsilon , right) = 0.}$

Интерпретируя этот результат, слабый закон утверждает, что для любого заданного ненулевого запаса, независимо от того, насколько он мал, с достаточно большой выборкой будет очень высокая вероятность того, что среднее значение наблюдений будет близко к ожидаемому значению; то есть в пределах поля.

Как упоминалось ранее, слабый закон применяется в случае i.i.d. случайные величины, но это применимо и в некоторых других случаях. Например, дисперсия может быть разной для каждой случайной переменной в ряду, при этом ожидаемое значение остается постоянным. Если отклонения ограничены, то применяется закон, как показано Чебышев еще в 1867 г. (Если ожидаемые значения меняются в течение ряда, то мы можем просто применить закон к среднему отклонению от соответствующих ожидаемых значений. Затем закон гласит, что это сходится по вероятности к нулю.) Фактически, доказательство Чебышева работает до тех пор, пока дисперсия среднего первого п значения стремятся к нулю как п уходит в бесконечность.^[12] В качестве примера предположим, что каждая случайная величина в серии следует за Гауссово распределение со средним нулем, но с дисперсией, равной ${ Displaystyle 2n / журнал (п + 1)}$, который не ограничен. На каждом этапе среднее значение будет нормально распределенным (как среднее значение набора нормально распределенных переменных). Дисперсия суммы равна сумме дисперсий, которая равна асимптотический к ${ Displaystyle п ^ {2} / журнал п}$. Следовательно, дисперсия среднего асимптотика ${ Displaystyle 1 / журнал п}$ и уходит в ноль.

Есть также примеры применения слабого закона, даже если ожидаемого значения не существует.

Сильный закон

В сильный закон больших чисел заявляет, что выборочное среднее сходится почти наверняка к ожидаемому значению^[16]

${ displaystyle { begin {matrix} {} { overline {X}} _ {n} xrightarrow { text {as}} mu qquad { textrm {when}} n to infty. {} end {matrix}}}$

(закон. 3)

Это,

${ displaystyle Pr ! left ( lim _ {n to infty} { overline {X}} _ {n} = mu right) = 1.}$

Это означает, что вероятность того, что количество испытаний п уходит в бесконечность, среднее из наблюдений сходится к ожидаемому значению, равному единице.

Доказательство более сложное, чем доказательство слабого закона.^[17] Этот закон оправдывает интуитивную интерпретацию ожидаемого значения (только для интегрирования Лебега) случайной величины при повторной выборке как «долгосрочное среднее».

Почти наверное сходимость также называется сильной сходимостью случайных величин. Эта версия называется усиленным законом, потому что случайные величины, которые сходятся сильно (почти наверняка), гарантированно сходятся слабо (по вероятности). Однако известно, что слабый закон выполняется в определенных условиях, когда сильный закон не выполняется, и тогда сходимость является только слабой (по вероятности). Увидеть # Различия между слабым и сильным законом.

Сам по себе усиленный закон больших чисел можно рассматривать как частный случай поточечно эргодическая теорема.

Сильный закон применяется к независимым одинаково распределенным случайным величинам, имеющим ожидаемое значение (например, слабый закон). Это было доказано Колмогоровым в 1930 году. Это применимо и в других случаях. Колмогоров также показал в 1933 году, что если переменные независимы и одинаково распределены, то среднее почти наверняка сходится на что нибудь (это можно считать еще одним утверждением сильного закона), необходимо, чтобы они имели ожидаемое значение (и тогда, конечно, среднее почти наверняка будет сходиться с ним).^[18]

Если слагаемые независимы, но не распределены одинаково, то

${ displaystyle { overline {X}} _ {n} - operatorname {E} { big [} { overline {X}} _ {n} { big]} { xrightarrow { text {как }}} 0,}$

при условии, что каждый Икс_k имеет конечный второй момент и

${ displaystyle sum _ {k = 1} ^ { infty} { frac {1} {k ^ {2}}} operatorname {Var} [X_ {k}] < infty.}$

Это заявление известно как Сильный закон Колмогоровасм. например Сен и певец (1993, Теорема 2.3.10).

Пример серии, в которой применяется слабый закон, но не сильный, - это когда Икс_k плюс или минус ${ displaystyle { sqrt {k / log log log k}}}$ (начиная с достаточно большого k так что знаменатель положительный) с вероятностью 1/2 для каждого.^[18] Дисперсия Икс_k затем ${ Displaystyle к / журнал журнал журнал к.}$ Строгий закон Колмогорова неприменим, поскольку частичная сумма в его критерии до к = п асимптотичен ${ Displaystyle журнал п / журнал журнал журнал п}$ и это безгранично.

Если мы заменим случайные величины на гауссовские переменные с такой же дисперсией, а именно ${ displaystyle { sqrt {k / log log log k}},}$ тогда среднее значение в любой точке также будет нормально распределено. Ширина распределения среднего будет стремиться к нулю (асимптотика стандартного отклонения ${ displaystyle 1 / { sqrt {2 log log log n}}}$), но для данного ε существует вероятность, которая не стремится к нулю при п, в то время как в среднем через некоторое время после п-ое испытание вернется к ε. Поскольку ширина распределения среднего не равна нулю, оно должно иметь положительную нижнюю границу. п(ε), что означает, что существует вероятность не менее п(ε), что среднее значение достигнет ε после п испытания. Это произойдет с вероятностью п(ε) / 2 перед некоторыми м что зависит от п. Но даже после м, остается вероятность не менее п(ε), что это произойдет. (Это, кажется, указывает на то, что п(ε) = 1, и среднее будет достигать ε бесконечное число раз.)

Различия между слабым законом и сильным законом

В слабый закон заявляет, что для указанного большого п, среднее ${ displaystyle { overline {X}} _ {n}}$ вероятно будет рядом μ. Таким образом, остается возможность, что ${ displaystyle | { overline {X}} _ {n} - mu |> varepsilon}$ происходит бесконечное количество раз, хотя и с нечастыми интервалами. (Не обязательно ${ displaystyle | { overline {X}} _ {n} - mu | neq 0}$ для всех п).

В строгий закон показывает, что это почти наверняка не произойдет. В частности, это означает, что с вероятностью 1 мы имеем это для любого ε > 0 неравенство ${ displaystyle | { overline {X}} _ {n} - mu | < varepsilon}$ держит для всех достаточно больших п.^[19]

Сильный закон не выполняется в следующих случаях, но слабый закон выполняется.^[20][21][22]

1. Пусть X - экспоненциально распределенная случайная величина с параметром 1. Случайная величина ${ Displaystyle грех (X) е ^ {X} X ^ {- 1}}$ не имеет ожидаемого значения согласно интегрированию Лебега, но использует условную сходимость и интерпретирует интеграл как Интеграл Дирихле, что является неправильным Интеграл Римана, мы можем сказать:

${ displaystyle E left ({ frac { sin (X) e ^ {X}} {X}} right) = int _ {0} ^ { infty} { frac { sin (x ) e ^ {x}} {x}} e ^ {- x} dx = { frac { pi} {2}}}$

2. Пусть x будет геометрическое распределение с вероятностью 0,5. Случайная величина ${ Displaystyle 2 ^ {X} (- 1) ^ {X} X ^ {- 1}}$ не имеет ожидаемого значения в общепринятом смысле, потому что бесконечное серии не является абсолютно сходящимся, но, используя условную сходимость, мы можем сказать:

${ displaystyle E left ({ frac {2 ^ {X} (- 1) ^ {X}} {X}} right) = sum _ {1} ^ { infty} { frac {2 ^ {x} (- 1) ^ {x}} {x}} 2 ^ {- x} = - ln (2)}$

3. Если кумулятивная функция распределения случайной величины

${ displaystyle 1-F (x) = { frac {e} {2x ln (x)}}, x geq e}$

${ Displaystyle F (x) = { frac {e} {- 2x ln (-x)}}, x leq -e}$

тогда он не имеет ожидаемого значения, но слабый закон верен.^[23][24]

Единый закон больших чисел

Предположим ж(Икс,θ) это некоторые функция определены для θ ∈ Θ и непрерывна по θ. Тогда для любого фиксированного θ, последовательность {ж(Икс₁,θ), ж(Икс₂,θ), ...} будет последовательностью независимых и одинаково распределенных случайных величин, такой, что выборочное среднее этой последовательности сходится по вероятности к E [ж(Икс,θ)]. Это точечно (в θ) сходимость.

В единый закон больших чисел устанавливает условия, при которых происходит сходимость равномерно в θ. Если^[25][26]

1. Θ компактно,
2. ж(Икс,θ) непрерывна на каждом θ ∈ Θ для почти все Иксs, и измеримая функция Икс на каждом θ.
3. существует доминирующий функция d(Икс) такое, что E [d(Икс)] <∞, и

   ${ Displaystyle left | е (х, theta) right | leq d (x) quad { text {для всех}} theta in Theta.}$

Тогда E [ж(Икс,θ)] непрерывна в θ, и

${ displaystyle sup _ { theta in Theta} left | { frac {1} {n}} sum _ {i = 1} ^ {n} f (X_ {i}, theta) - operatorname {E} [f (X, theta)] right | { xrightarrow { mathrm {as}}} 0.}$

Этот результат полезен для получения согласованности большого класса оценок (см. Экстремальная оценка).

Закон больших чисел Бореля

Закон больших чисел Бореля, названный в честь Эмиль Борель, заявляет, что если эксперимент повторяется большое количество раз, независимо при идентичных условиях, то доля раз, когда любое указанное событие происходит, приблизительно равна вероятности возникновения события в любом конкретном испытании; чем больше количество повторений, тем лучше приближение. Точнее, если E обозначает рассматриваемое событие, п вероятность его появления, и N_п(E) количество раз E происходит в первом п испытания, то с вероятностью один,^[27]

${ displaystyle { frac {N_ {n} (E)} {n}} to p { text {as}} n to infty.}$

Эта теорема укрепляет интуитивное понятие вероятности как долгосрочную относительную частоту возникновения события. Это частный случай любого из нескольких более общих законов больших чисел в теории вероятностей.

Неравенство Чебышева. Позволять Икс быть случайная переменная с конечным ожидаемое значение μ и конечное ненулевое отклонение σ². Тогда для любого настоящий номер k > 0,

${ displaystyle Pr (| X- mu | geq k sigma) leq { frac {1} {k ^ {2}}}.}$

Доказательство слабого закона

Данный Икс₁, Икс₂, ... бесконечная последовательность i.i.d. случайные величины с конечным ожидаемым значением E(Икс₁) = E(Икс₂) = ... = µ <∞, нас интересует сходимость выборочного среднего

${ displaystyle { overline {X}} _ {n} = { tfrac {1} {n}} (X_ {1} + cdots + X_ {n}).}$

Слабый закон больших чисел гласит:

Теорема: ${ displaystyle { begin {matrix} {} { overline {X}} _ {n} { xrightarrow {P}} mu qquad { textrm {when}} n to infty . {} end {matrix}}}$

(закон. 2)

Доказательство с использованием неравенства Чебышева в предположении конечной дисперсии

Это доказательство использует предположение конечности отклонение ${ displaystyle operatorname {Var} (X_ {i}) = sigma ^ {2}}$ (для всех ${ displaystyle i}$). Независимость случайных величин подразумевает отсутствие корреляции между ними, и мы имеем

${ displaystyle operatorname {Var} ({ overline {X}} _ {n}) = operatorname {Var} ({ tfrac {1} {n}} (X_ {1} + cdots + X_ {n })) = { frac {1} {n ^ {2}}} operatorname {Var} (X_ {1} + cdots + X_ {n}) = { frac {n sigma ^ {2}} {n ^ {2}}} = { frac { sigma ^ {2}} {n}}.}$

Общее среднее значение μ последовательности - это среднее значение выборочного среднего:

${ Displaystyle E ({ overline {X}} _ {n}) = mu.}$

С помощью Неравенство Чебышева на ${ displaystyle { overline {X}} _ {n}}$ приводит к

${ displaystyle operatorname {P} ( left | { overline {X}} _ {n} - mu right | geq varepsilon) leq { frac { sigma ^ {2}} {n варепсилон ^ {2}}}.}$

Это может быть использовано для получения следующего:

${ displaystyle operatorname {P} ( left | { overline {X}} _ {n} - mu right | < varepsilon) = 1- operatorname {P} ( left | { overline {X }} _ {n} - mu right | geq varepsilon) geq 1 - { frac { sigma ^ {2}} {n varepsilon ^ {2}}}.}$

Так как п приближается к бесконечности, выражение приближается к 1. И по определению сходимость по вероятности, мы получили

${ displaystyle { begin {matrix} {} { overline {X}} _ {n} { xrightarrow {P}} mu qquad { textrm {when}} n to infty . {} end {matrix}}}$

(закон. 2)

Доказательство с использованием сходимости характеристических функций.

От Теорема Тейлора для сложные функции, то характеристическая функция любой случайной величины, Икс, с конечным средним μ, можно записать как

${ displaystyle varphi _ {X} (t) = 1 + it mu + o (t), quad t rightarrow 0.}$

Все Икс₁, Икс₂, ... имеют одну и ту же характеристическую функцию, поэтому обозначим это просто φ_Икс.

Среди основных свойств характеристических функций:

${ displaystyle varphi _ {{ frac {1} {n}} X} (t) = varphi _ {X} ({ tfrac {t} {n}}) quad { text {и}} quad varphi _ {X + Y} (t) = varphi _ {X} (t) varphi _ {Y} (t) quad}$ если Икс и Y независимы.

Эти правила можно использовать для вычисления характеристической функции ${ displaystyle scriptstyle { overline {X}} _ {n}}$ с точки зрения φ_Икс:

${ displaystyle varphi _ {{ overline {X}} _ {n}} (t) = left [ varphi _ {X} left ({t over n} right) right] ^ {n } = left [1 + i mu {t over n} + o left ({t over n} right) right] ^ {n} , rightarrow , e ^ {it mu} , quad { text {as}} quad n rightarrow infty.}$

Пределе^Этоμ - характеристическая функция постоянной случайной величины μ, и, следовательно, по Теорема Леви о непрерывности, ${ displaystyle scriptstyle { overline {X}} _ {n}}$ сходится в распределении к μ:

${ displaystyle { overline {X}} _ {n} , { xrightarrow { mathcal {D}}} , mu qquad { text {for}} qquad n to infty.}$

μ - константа, из которой следует, что сходимость по распределению к μ и сходимость по вероятности к μ эквивалентны (см. Сходимость случайных величин.) Следовательно,

${ displaystyle { begin {matrix} {} { overline {X}} _ {n} { xrightarrow {P}} mu qquad { textrm {when}} n to infty . {} end {matrix}}}$

(закон. 2)

Это показывает, что выборочное среднее сходится по вероятности к производной характеристической функции в начале координат, пока последняя существует.

Последствия

Закон больших чисел обеспечивает ожидание неизвестного распределения от реализации последовательности, но также и любой особенности распределения вероятностей.^[1] Применяя Закон больших чисел Бореля, можно легко получить функцию массы вероятности. Для каждого события в целевой функции вероятности и масс можно аппроксимировать вероятность возникновения события пропорциональностью того, сколько раз происходит любое указанное событие. Чем больше количество повторов, тем лучше приближение. Что касается непрерывного случая: ${ Displaystyle С = (а-ч, а + ч]}$, для небольшого положительного h. Таким образом, для больших n:

${ Displaystyle { гидроразрыва {N_ {n} (C)} {n}} Thickapprox p = P (X in C) = int _ {ah} ^ {a + h} f (x) dx Thickapprox 2hf (а)}$

С помощью этого метода можно покрыть всю ось x сеткой (с размером сетки 2h) и получить гистограмму, которая называется гистограмма.

Смотрите также

• Асимптотическое свойство равнораспределения
• Центральная предельная теорема
• Теорема о бесконечной обезьяне
• Закон средних чисел
• Закон повторного логарифма
• Закон действительно больших чисел
• Линди эффект
• Регресс к среднему
• Сортировка

Заметки

использованная литература

внешние ссылки

• «Закон больших чисел», Энциклопедия математики, EMS Press, 2001 [1994]
• Вайсштейн, Эрик В. «Слабый закон больших чисел». MathWorld.
• Вайсштейн, Эрик В. «Сильный закон больших чисел». MathWorld.
• Анимации для закона больших чисел Ихуи Се с помощью р пакет анимация
• Генеральный директор Apple Тим Кук сказал то, что заставило бы статистиков съежиться. «Мы не верим в такие законы, как законы больших чисел. Я думаю, это своего рода старая догма, которую кто-то придумал [..]», - сказал Тим Кук, а затем: «Однако закон больших чисел не имеет ничего общего с крупными компаниями, большими доходами или высокими темпами роста. Закон больших чисел является фундаментальной концепцией в теории вероятностей и статистике, связывая вместе теоретические вероятности, которые мы можем вычислить, с фактическими результатами экспериментов, которые мы эмпирически выполнить. объяснил Business Insider