WikiDer > Магический шестиугольник

Magic hexagon

Заказ n = 3
M = 38

А магический шестиугольник порядка п это расположение чисел в гексагональный узор по центру с участием п ячейки на каждом краю таким образом, чтобы числа в каждой строке во всех трех направлениях суммировались одинаково магическая константа M. А нормальный магический шестиугольник содержит последовательный целые числа от 1 до 3п² − 3п + 1. Получается, что нормальные магические шестиугольники существуют только для п = 1 (что тривиально, так как состоит всего из одного шестиугольника) и п = 3. Более того, решение порядка 3 практически единственно.^[1] Мэн также дал менее сложное конструктивное доказательство.^[2]

Магический шестиугольник порядка 3 много раз публиковался как «новое» открытие. Первым упоминанием и, возможно, первым первооткрывателем является Эрнст фон Хазельберг (1887).

Доказательство нормальных магических шестиугольников

Цифры в шестиугольнике идут подряд от 1 до ${ displaystyle (3n ^ {2} -3n + 1)}$ . Следовательно, их сумма равна треугольное число, а именно

{ displaystyle s = {1 over {2}} (3n ^ {2} -3n + 1) (3n ^ {2} -3n + 2) = {9n ^ {4} -18n ^ {3} + 18n ^ {2} -9n + 2 более {2}}}

Есть р = (2п - 1) ряды, идущие в любом заданном направлении (В-З, СВ-Ю или СЗ-ЮВ). Сумма каждой из этих строк равна одному и тому же числу M. Следовательно:

{ Displaystyle M = {s over {r}} = {9n ^ {4} -18n ^ {3} + 18n ^ {2} -9n + 2 over {2 (2n-1)}}}

Это можно переписать как

{ displaystyle M = left ({ frac {9n ^ {3}} {4}} - { frac {27n ^ {2}} {8}} + { frac {45n} {16}} - { frac {27} {32}} right) + { frac {5} {32 left (2n-1 right)}}}

Умножение на 32 дает

{ displaystyle 32M = 72n ^ {3} -108n ^ {2} + 90n-27 + {5 over 2n-1}}

что показывает, что ${ displaystyle { frac {5} {2n-1}}}$ должно быть целым числом, следовательно, 2n-1 должно быть множителем 5, а именно 2n-1 = 1 или 2n-1 = 5. Единственный ${ Displaystyle п geq 1}$ которые соответствуют этому условию ${ Displaystyle п = 1}$ и ${ displaystyle n = 3}$ , что доказывает, что не существует нормальных магических шестиугольников, кроме первого и третьего порядка.

Аномальные магические шестиугольники

Хотя не существует нормальных магических шестиугольников с порядком выше 3, некоторые аномальные существуют. В данном случае ненормальное означает начало последовательности чисел, отличных от 1. Арсен Захрей обнаружил эти шестиугольники порядка 4 и 5:


Заказ 4 M = 111	Заказ 5 M = 244

Шестиугольник четвертого порядка начинается с 3 и заканчивается 39, сумма строк в нем составляет 111. Шестиугольник пятого порядка начинается с 6 и заканчивается 66 и в сумме составляет 244.

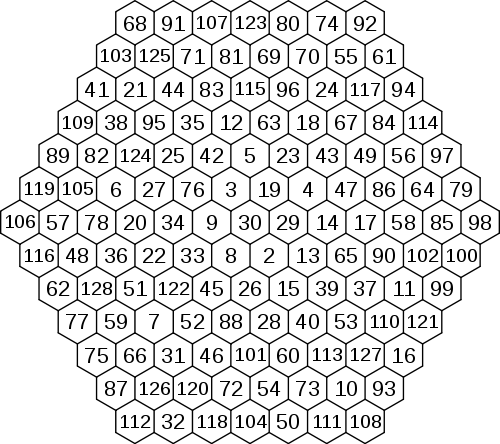
Шестиугольник порядка 5, начинающийся с 15, заканчивающийся 75 и суммируемый до 305, выглядит следующим образом:

         56  61  70  67  51       55  45  36  48  53  68     74  37  26  29  27  39  73   62  42  33  19  16  31  38  64 58  57  22  20  15  18  23  43  49   63  47  28  21  17  30  34  65     71  35  24  32  25  46  72       59  44  40  41  52  69         54  60  75  66  50

Сумма, превышающая 305 для шестиугольников порядка 5, невозможна.

Шестиугольники порядка 5, где «X» - заполнители для шестиугольников порядка 3, которые завершают числовую последовательность. В верхнем уместится шестиугольник с суммой 38 (числа от 1 до 19), а в нижнем - из 26 шестиугольников с суммой 0 (числа от -9 до 9). (для получения дополнительной информации посетите Немецкая статья в Википедии)

        39 35-14 21-20-16-12 37 22 34-4 XXX -5-7-1 36 XXXX -13-17 30 23X XXXX -6 24-21 26 XXXX -3 0 28-2 XXX 27-11 - 18 25-15-9 33-8 29 31 38 32-10 20-19 30 28-18-13-27-30-28 18 15 13 12 XXX 27 21-22-26 XXXX -11-24 16 19X XXXX - 12 10-20 22 XXXX -16-21 11 26 XXX 20 14-19-15-29-25 17 24 23-10 29 25-17-14-23

Шестиугольник порядка 6 можно увидеть ниже. Его создал Луи Хелблинг, 11 октября 2004 г .:

Он начинается с 21, заканчивается на 111, а его сумма равна 546.

Этот волшебный шестиугольник 7-го порядка был обнаружен Арсеном Захреем 22 марта 2006 года с помощью моделированного отжига:

Он начинается с 2, заканчивается 128, а его сумма равна 635.

Магический шестиугольник порядка 8 был создан Луи К. Хелблингом 5 февраля 2006 года:

Он начинается с -84 и заканчивается 84, а его сумма равна 0.

Волшебные Т-образные шестиугольники

Шестиугольники также могут быть построены из треугольников, как показано на следующих диаграммах.


Заказ 2	Заказ 2 с номерами 1–24

Этот тип конфигурации можно назвать Т-образным шестиугольником, и он имеет гораздо больше свойств, чем шестиугольник шестиугольников.

Как и в предыдущем случае, ряды треугольников проходят в трех направлениях, и есть 24 треугольника в Т-шестиугольнике порядка 2. Как правило, Т-шестиугольник порядка п имеет ${ displaystyle 6n ^ {2}}$ треугольники. Сумма всех этих чисел определяется как:

{ Displaystyle S = 3n ^ {2} (6n ^ {2} +1)}

Если мы попытаемся построить волшебный Т-образный шестиугольник со стороной п, мы должны выбрать п быть ровным, потому что есть $р = 2 п$ строк, поэтому сумма в каждой строке должна быть

{ displaystyle M = { frac {S} {R}} = { frac {3n ^ {2} (6n ^ {2} +1)} {2n}}}

Чтобы это было целое число, п должно быть даже. На сегодняшний день открыты волшебные Т-шестиугольники 2, 4, 6 и 8 порядка. Первым был магический Т-шестиугольник порядка 2, открытый Джоном Бейкером 13 сентября 2003 года. С тех пор Джон сотрудничал с Дэвидом Кингом, который обнаружил 59 674 527 несовпадающих магических Т-шестиугольников порядка 2.

Магические Т-образные шестиугольники обладают рядом свойств, общих с магическими квадратами, но у них также есть свои особенности. Самым удивительным из них является то, что сумма чисел в треугольниках, указывающих вверх, такая же, как и сумма чисел в треугольниках, направленных вниз (независимо от размера Т-шестиугольника). В приведенном выше примере

17 + 20 + 22 + 21 + 2 + 6 + 10 + 14 + 3 + 16 + 12 + 7

= 5 + 11 + 19 + 9 + 8 + 13 + 4 + 1 + 24 + 15 + 23 + 18

= 150

Заметки

^ Тригг, К.В. «Уникальный магический шестиугольник», Журнал развлекательной математики, Январь – февраль 1964. Проверено 16 декабря 2009 г.
^ <Мэн, Ф. "Исследование магического шестиугольника Порядка 3", Награды Шинг-Тунг Яу, Октябрь 2008. Проверено 16 декабря 2009 г.

использованная литература

Бейкер. Дж. Э. и Кинг Д. Р. (2004) «Использование визуальной схемы для определения свойств шестиугольника» Визуальная математика, том 5, номер 3
Бейкер, Дж. Э. и Бейкер, А. Дж. (2004) «Шестиугольник, выбор природы» Архимед, том 4

Смотрите также

[1] Тригг, К.В. «Уникальный магический шестиугольник», Журнал развлекательной математики, Январь – февраль 1964. Проверено 16 декабря 2009 г.

[2] <Мэн, Ф. "Исследование магического шестиугольника Порядка 3", Награды Шинг-Тунг Яу, Октябрь 2008. Проверено 16 декабря 2009 г.

[1]

[2]

v т е Магические многоугольники
Типы	Магический круг Магический шестиугольник Магическая гексаграмма Магический квадрат Волшебная звезда Магический треугольник
Связанные фигуры	Альфа-магический квадрат Антимагический квадрат Геомагический квадрат Гетероквадрат Пандиагональный магический квадрат Самый совершенный магический квадрат
Формы более высоких размеров	Волшебный куб классы Магический гиперкуб Магический гиперпучок
Классификация	Ассоциативный магический квадрат Пандиагональный магический квадрат Мультимагический квадрат
Связанные понятия	Латинский квадрат Слово квадрат Number Scrabble Пазл о восьми ферзях Магическая константа Магический граф Волшебная серия

Navigation