WikiDer > Классы магического куба

Эта статья возможно содержит оригинальные исследования. Пожалуйста Улучши это к проверка заявленные претензии и добавление встроенные цитаты. Заявления, содержащие только оригинальные исследования, следует удалить. (Июнь 2012 г.) (Узнайте, как и когда удалить этот шаблон сообщения)

Каждый волшебный куб может быть отнесен к одному из шести классы магического куба, исходя из характеристик куба.

Эта новая система более точно определяет магические кубики. Но, что, возможно, более важно, он одинаков для всех заказов и всех размеров магические гиперкубы.

Минимальные требования Для того, чтобы куб был волшебным, следующие: все строки, столбцы, столбы и 4 треугольника должны в сумме давать одно и то же значение.

Шесть классов

• Простой:

Минимальные требования для магического куба: Сумма всех строк, столбцов, столбов и четырех треугольников должна быть одинаковой. А Простой волшебный куб не содержит магических квадратов или недостаточно, чтобы претендовать на следующий класс.
Наименьший нормальный простой магический куб имеет порядок 3. Минимально необходимое правильное суммирование = 3м² + 4

• Диагональ:

Каждый из 3м плоские массивы должны быть простой магический квадрат. 6 наклонных квадратов - тоже простая магия. Наименьший нормальный диагональный магический куб имеет порядок 5.
Эти квадраты были названы Гарднером и другими «идеальными»! В то же время он назвал пандиагональный куб Ленгмана 1962 года «Совершенным».
Кристиан Бойер и Уолтер Трамп теперь рассматривают это и следующие два класса будут Идеально. (Видеть Альтернативный идеальный ниже).
А. Х. Фрост называл все классы, кроме простых, Насик кубики.
Наименьший нормальный диагональный магический куб имеет порядок 5. См. Диагональный магический куб. Требуется минимальное количество правильных сумм = 3м² + 6м + 4

• Пантриагональ:

Все 4м² пантриагонали должны суммироваться правильно (то есть 4 односегментных, 12 (м-1) двухсегментный и 4 (м-2)(м-1) трехсегментный). Может быть несколько простых пандиагональных магических квадратов И / ИЛИ, но их недостаточно, чтобы удовлетворить любую другую классификацию.
Наименьший нормальный пантриагональный магический куб имеет порядок 4. См. Пантриагональный магический куб.
Требуется минимальное количество правильных сумм = 7м². Все пан-р-агонали суммируются правильно для р = 1 и 3.

• PantriagDiag:

Куб этого класса был впервые построен в конце 2004 года Мицутоси Накамура. Этот куб представляет собой комбинацию Пантриагональный магический куб и Диагональный магический куб. Поэтому все основное и сломанное триагонали сумма правильно, и она содержит 3м планарный простые магические квадраты. Кроме того, все 6 наклонных квадратов пандиагональные магические квадраты. Единственный такой куб, построенный на данный момент, - это порядок 8. Неизвестно, какие другие порядки возможны. Видеть Магический куб Pantriagdiag. Требуется минимальное количество правильных сумм = 7м² + 6м

• Пандиагональ:

ВСЕ 3м плоские массивы должны быть пандиагональные магические квадраты. 6 наклонных квадратов всегда магические (обычно простая магия). Некоторые из них МОГУТ быть пандиагональной магией. Гарднер также назвал этот (пандиагональный) куб Ленгмана «идеальным» кубом, по-видимому, не осознавая, что это более высокий класс, чем куб Майера. См. Предыдущую заметку о Бойе и Трампе.
Наименьший нормальный пандиагональный магический куб имеет порядок 7. См. Пандиагональный магический куб.
Требуется минимальное количество правильных сумм = 9м² + 4. Все пан-р-агонали суммируются правильно для р = 1 и 2.

• Идеально:

ВСЕ 3м плоские массивы должны быть пандиагональные магические квадраты. Кроме того, ВСЕ пантриагонали должны правильно суммироваться. Эти два условия в совокупности дают в общей сложности 9 миллионов пандиагональных магических квадратов.
Наименьший нормальный совершенный магический куб имеет порядок 8. См. Идеальный волшебный куб.

Насик;А. Х. Фрост (1866) называл Насиком всех, кроме простого магического куба!
К. Планк (1905) переосмыслил Насик означать магические гиперкубы любого порядка и размерности, в которых правильно суммированы все возможные линии.
т.е. Насик это предпочтительный вариант, и менее двусмысленный термин для идеально учебный класс.
Требуется минимум правильных сумм = 13м². Все пан-р-агонали суммируются правильно для р = 1, 2 и 3.

Альтернативный идеальныйОбратите внимание, что приведенное выше определение термина идеально. Примерно до 1995 года было много путаницы в том, что представляет собой идеально магический куб (см. обсуждение под диагональ:)
. Ниже приведены ссылки и ссылки на обсуждения старого определения.
С ростом популярности персональных компьютеров стало легче исследовать мельчайшие детали волшебных кубов. Также все больше и больше работ было сделано с магическими гиперкубами более высоких измерений. Например, Джон Хендрикс построил первый в мире Насик магический тессеракт в 2000 году. Классифицирован как идеальный магический тессеракт по определению Хендрикса.

Обобщено для всех измерений

Волшебный гиперкуб измерения п идеально, если сумма всех пан-n-агоналей правильно. Тогда все содержащиеся в нем гиперкубы более низкой размерности также совершенны.
Для измерения 2 Пандиагональный Магический Квадрат был назван идеально на протяжении многих лет. Это согласуется с определениями perfect (nasik), данными выше для куба. В этом измерении нет двусмысленности, потому что существует только два класса магических квадратов: простые и совершенные.
В случае четырех измерений, магического тессеракта, Мицутоши Накамура определил, что существует 18 классов. Он определил их характеристики и построил примеры каждого из них. Идеально (насик) В магическом тессеракте правильно суммируются все возможные линии, и все кубики и квадраты, содержащиеся в нем, также являются насик-магией.

Другое определение и таблица

Правильный:Правильный магический куб - это магический куб, принадлежащий к одному из шести классов магических кубов, но содержащий в точности минимальные требования для этого класса куба. т.е. правильный простой или пятиугольный магический куб не будет содержать магических квадратов, правильный диагональный магический куб будет содержать ровно 3м + 6 простых магических квадратов и др. Этот термин был введен Мицутоси Накамурой в апреле 2004 года.

Примечания к таблице

1. Для диагональных или пандиагональных классов один или, возможно, 2 из 6 наклонных магических квадратов могут быть пандиагональной магией. Все, кроме 6 наклонных квадратов, «сломаны». Это аналогично разбитым диагоналям в пандиагональном магическом квадрате. т.е. разорванные диагонали - это 1-D в квадрате 2_D; ломаные косые квадраты - это двумерные в трехмерном кубе.
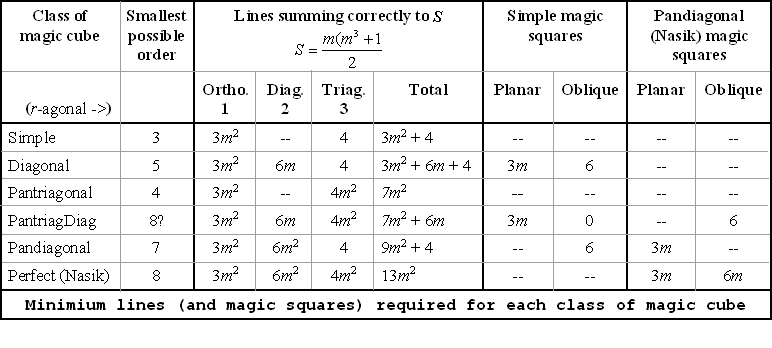
2. В таблице показано минимальное количество линий или квадратов, необходимых для каждого класса (т.е. надлежащего). Обычно их больше, но недостаточно одного типа, чтобы претендовать на следующий класс.

Смотрите также

• Магический гиперкуб
• Насик магический гиперкуб
• Панмагическая площадь
• Диагональ пространства
• Джон Р. Хендрикс

Рекомендации

Эта статья не цитировать любой источники. Пожалуйста помоги улучшить эту статью к добавление цитат в надежные источники. Материал, не полученный от источника, может быть оспорен и удаленный. Найдите источники: «Классы магического куба» – Новости · газеты · книги · ученый · JSTOR (Июль 2008 г.) (Узнайте, как и когда удалить этот шаблон сообщения)

дальнейшее чтение

• Фрост, доктор А. Х., Об общих свойствах кубиков Насика, QJM 15, 1878, стр. 93–123.
• Планк К., Theory of Paths Nasik, Отпечатано для частного обращения, A.J. Лоуренс, принтер, регби (Англия), 1905 г.
• Хайнц, Х. и Хендрикс, Дж. Р., Magic Square Lexicon: Illustrated. Самостоятельно опубликовано, 2000 г., 0-9687985-0-0.
• Хендрикс, Джон Р., Пан-4-агональный магический тессеракт, The American Mathematical Monthly, Vol. 75, No. 4, апрель 1968 г., стр. 384.
• Хендрикс, Джон Р., Пан-3-агональный магический куб, Журнал развлекательной математики, 5: 1, 1972, стр. 51–52.
• Хендрикс, Джон Р., Пан-3-агональный Магический Куб Порядка-5, JRM, 5: 3, 1972, стр 205–206
• Хендрикс, Джон Р., Компьютерные магические квадраты и тессеракты, самоиздан, 1999. 0-9684700-0-9
• Хендрикс, Джон Р., Совершенные n-мерные магические гиперкубы порядка 2n, самоиздание, 1999. 0-9684700-4-1
• Клиффорд А. Пиковер (2002). Дзен магических квадратов, кругов и звезд. Princeton Univ. Press, 2002, 0-691-07041-5. стр. 101–121

внешняя ссылка

Кубические классы

• Кристиан Бойер: Совершенные волшебные кубики
• Харви Хайнц: Совершенные волшебные гиперкубы
• Харви Хайнц: 6 классов кубиков
• Уолтер Трамп: в поисках самого маленького
• Самый совершенный куб

Идеальный куб

• Аале де Винкель: Магическая энциклопедия
• Длинная цитата из К. Планка (1917) на тему насик как заменяющий термин для идеально.

Классы Tesseract

• Классы Square, Cube и Tesseract