А неогуковское твердое тело[1] это сверхупругий материал модель, похожая на Закон Гука, который можно использовать для прогнозирования нелинейного поведения напряженно-деформированного материала в материалах, подвергающихся большим деформации. Модель была предложена Рональд Ривлин в 1948 году. В отличие от линейная эластичность материалы, кривая напряжения-деформации неогуковского материала не линейный. Вместо этого зависимость между приложенным напряжением и деформацией изначально является линейной, но в определенный момент кривая напряжения-деформации выйдет на плато. Неогуковская модель не учитывает диссипативный выделение энергии в виде тепла при деформации материала и совершенная эластичность предполагается на всех этапах деформации.
Модель нео-Гука основана на статистической термодинамике сшитых полимерных цепей и может использоваться для пластмассы и резинка-подобные вещества. Сшитые полимеры будут действовать неогуковским образом, потому что первоначально полимерные цепи могут перемещаться относительно друг друга при приложении напряжения. Однако в определенный момент полимерные цепи будут растянуты до максимальной точки, допускаемой ковалентными поперечными связями, и это вызовет резкое увеличение модуля упругости материала. Неогуковская модель материала не предсказывает это увеличение модуля при больших деформациях и обычно точна только для деформаций менее 20%.[2] Модель также неадекватна для двухосных напряженных состояний и была заменена Муни-Ривлин модель.
В функция плотности энергии деформации для несжимаемый неогуковский материал в трехмерном описании

куда  - материальная постоянная, а
- материальная постоянная, а  это первый инвариант (след), из правый тензор деформации Коши-Грина, т.е.
это первый инвариант (след), из правый тензор деформации Коши-Грина, т.е.

куда  являются основные участки.[1]
являются основные участки.[1]
Для сжимаемый В неогуковском материале функция плотности энергии деформации определяется выражением

куда  материальная постоянная и
материальная постоянная и  это градиент деформации. Можно показать, что в 2D функция плотности энергии деформации имеет вид
это градиент деформации. Можно показать, что в 2D функция плотности энергии деформации имеет вид

Существует несколько альтернативных составов сжимаемых материалов неогуковского периода, например:

куда  это первый инвариант из изохорный часть
это первый инвариант из изохорный часть  из правый тензор деформации Коши – Грина.
из правый тензор деформации Коши – Грина.
Для однородности с линейной эластичностью,

куда  модуль сдвига или первый Параметры Ламе и
модуль сдвига или первый Параметры Ламе и  это объемный модуль.[3]
это объемный модуль.[3]
Напряжение Коши в терминах тензоров деформации
Сжимаемый материал в стиле нео-Гук
Для сжимаемого неогуковского материала Ривлина напряжение Коши определяется выражением

куда  - левый тензор деформации Коши - Грина, а
- левый тензор деформации Коши - Грина, а

Для бесконечно малых деформаций ( )
)

а напряжение Коши можно выразить как

В сравнении с Закон Гука показывает, что  и
и  .
.
| Доказательство: |
|---|
В Напряжение Коши в сжимаемый сверхупругий материал определяется выражением ![{ displaystyle { boldsymbol { sigma}} = { cfrac {2} {J}} left [{ cfrac {1} {J ^ {2/3}}} left ({ cfrac { partial {W}} { partial { bar {I}} _ {1}}} + { bar {I}} _ {1} ~ { cfrac { partial {W}} { partial { bar { I}} _ {2}}} right) { boldsymbol {B}} - { cfrac {1} {J ^ {4/3}}} ~ { cfrac { partial {W}} { partial { bar {I}} _ {2}}} ~ { boldsymbol {B}} cdot { boldsymbol {B}} right] + left [{ cfrac { partial {W}} { partial J}} - { cfrac {2} {3J}} left ({ bar {I}} _ {1} ~ { cfrac { partial {W}} { partial { bar {I}} _ {1}}} + 2 ~ { bar {I}} _ {2} ~ { cfrac { partial {W}} { partial { bar {I}} _ {2}}} right) справа] ~ { boldsymbol {I}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a02006f31ec08f5ff11d32479fcc80ae15ffb0ea)
Для сжимаемого материала Rivlin neo-Hookean, 
в то время как для сжимаемого материала Ogden neo-Hookean, 
Следовательно, напряжение Коши в сжимаемом материале Ривлина неогуковского типа определяется выражением ![{ displaystyle { boldsymbol { sigma}} = { cfrac {2} {J}} left [{ cfrac {1} {J ^ {2/3}}} ~ C_ {1} ~ { boldsymbol {B}} right] + left [2D_ {1} (J-1) - { cfrac {2} {3J}} ~ C_ {1} { bar {I}} _ {1} right] { boldsymbol {I}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/120f858b142ddd9ee4ad00a67d5fb3bb9b99c1ae)
в то время как для соответствующего материала Огдена ![{ displaystyle { boldsymbol { sigma}} = { cfrac {2} {J}} left [{ cfrac {1} {J ^ {2/3}}} ~ C_ {1} ~ { boldsymbol {B}} right] + left [2D_ {1} (J-1) - { cfrac {2C_ {1}} {J}} - { cfrac {2} {3J}} ~ C_ {1} { bar {I}} _ {1} right] { boldsymbol {I}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83d1614008549ca9e50b92d17563b2f0c2bcf4ac)
Если изохорный часть левого тензора деформации Коши - Грина определяется как  , то мы можем записать напряжение Ривлина нео-Хеукена как , то мы можем записать напряжение Ривлина нео-Хеукена как ![{ displaystyle { boldsymbol { sigma}} = { cfrac {2C_ {1}} {J}} left [{ bar { boldsymbol {B}}} - { tfrac {1} {3}} { bar {I}} _ {1} { boldsymbol {I}} right] + 2D_ {1} (J-1) { boldsymbol {I}} = { cfrac {2C_ {1}} {J }} operatorname {dev} ({ bar { boldsymbol {B}}}) + 2D_ {1} (J-1) { boldsymbol {I}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b584cedbf95ffa49a8e0ced00a2756041e5cc65)
и неогуковское напряжение Огдена как ![{ displaystyle { boldsymbol { sigma}} = { cfrac {2C_ {1}} {J}} left [{ bar { boldsymbol {B}}} - { tfrac {1} {3}} { bar {I}} _ {1} { boldsymbol {I}} - { boldsymbol {I}} right] + 2D_ {1} (J-1) { boldsymbol {I}} = { cfrac {2C_ {1}} {J}} left [ operatorname {dev} ({ bar { boldsymbol {B}}}) - { boldsymbol {I}} right] + 2D_ {1} (J- 1) { boldsymbol {I}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/336115e7026192205dd2f146f41c09e65b22caf8)
Количество 
иметь форму давление и обычно рассматриваются как таковые. Неогуковское напряжение Ривлина может быть выражено в форме 
в то время как неогуковское ударение Огдена имеет форму 
|
Несжимаемый материал в стиле нео-Гук
Для несжимаемый неогукейский материал с 

куда  неопределенное давление.
неопределенное давление.
Напряжение Коши в терминах главных растяжений
Сжимаемый материал неогукевского стиля
Для сжимаемого нео-гука сверхупругий материал, главные компоненты напряжения Коши задаются формулами
![sigma _ {{i}} = 2C_ {1} J ^ {{- 5/3}} left [ lambda _ {i} ^ {2} - { cfrac {I_ {1}} {3}} right] + 2D_ {1} (J-1) ~; ~~ i = 1,2,3](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1e8671c7cc3313e7f11cd4b42d7d466d7b4bf69)
Следовательно, разница между главными напряжениями составляет

| Доказательство: |
|---|
Для сжимаемого сверхупругий материал, главные компоненты напряжения Коши задаются формулами 
Функция плотности энергии деформации для сжимаемого неогуковского материала имеет вид ![W = C_ {1} ({ bar {I}} _ {1} -3) + D_ {1} (J-1) ^ {2} = C_ {1} left [J ^ {{- 2 / 3}} ( lambda _ {1} ^ {2} + lambda _ {2} ^ {2} + lambda _ {3} ^ {2}) - 3 right] + D_ {1} (J- 1) ^ {2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3080a7a8adbd13388160411dcb3347e301d86d0)
Следовательно, ![lambda _ {i} { frac { partial W} { partial lambda _ {i}}} = C_ {1} left [- { frac {2} {3}} J ^ {{- 5 / 3}} lambda _ {i} { frac { partial J} { partial lambda _ {i}}} ( lambda _ {1} ^ {2} + lambda _ {2} ^ {2 } + lambda _ {3} ^ {2}) + 2J ^ {{- 2/3}} lambda _ {i} ^ {2} right] + 2D_ {1} (J-1) lambda _ {i} { frac { partial J} { partial lambda _ {i}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87611cb53239ecb742121e0e9535183c69fc69b5)
С  у нас есть у нас есть 
Следовательно, ![{ begin {align} lambda _ {i} { frac { partial W} { partial lambda _ {i}}} & = C_ {1} left [- { frac {2} {3} } J ^ {{- 2/3}} ( lambda _ {1} ^ {2} + lambda _ {2} ^ {2} + lambda _ {3} ^ {2}) + 2J ^ {{ -2/3}} lambda _ {i} ^ {2} right] + 2D_ {1} J (J-1) & = 2C_ {1} J ^ {{- 2/3}} left [- { frac {1} {3}} ( lambda _ {1} ^ {2} + lambda _ {2} ^ {2} + lambda _ {3} ^ {2}) + lambda _ {i} ^ {2} right] + 2D_ {1} J (J-1) end {выравнивается}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c326c274fc12ae0344245cd5c390a34b06a6dd74)
Таким образом, главные напряжения Коши определяются выражением ![sigma _ {i} = 2C_ {1} J ^ {{- 5/3}} left [ lambda _ {i} ^ {2} - { cfrac {I_ {1}} {3}} right ] + 2D_ {1} (J-1)](https://wikimedia.org/api/rest_v1/media/math/render/svg/ceaecb06369b0b2869a0bb4180f929d238ef28c9)
|
Несжимаемый материал в стиле нео-Гук
Что касается основные участки, разности напряжений Коши для несжимаемый сверхупругий материал

Для несжимаемый неогукейский материал,

Следовательно,

который дает

Одноосное расширение
Сжимаемый материал неогукевского стиля
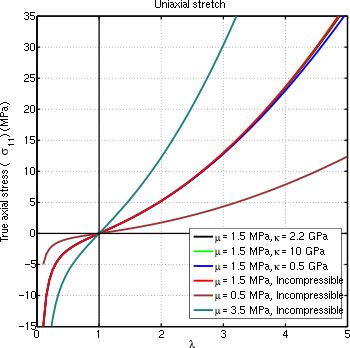
Истинное напряжение как функция одноосного растяжения, предсказанное сжимаемым материалом неогуковского периода для различных значений

. Свойства материала типичны для
натуральная резина.
Для сжимаемого материала, подвергающегося одноосному растяжению, основные растяжения равны

Следовательно, истинные напряжения (Коши) для сжимаемого неогуковского материала задаются выражением

Различия в напряжении представлены как

Если материал не ограничен, мы имеем  . потом
. потом

Приравнивая два выражения для  дает соотношение для
дает соотношение для  как функция
как функция  , т.е.
, т.е.

или же

Вышеупомянутое уравнение можно решить численно с помощью Ньютон-Рафсон итеративная процедура поиска корня.
Несжимаемый материал в стиле нео-Гук
При одноосном растяжении  и
и  . Следовательно,
. Следовательно,

Предполагая отсутствие тяги по бокам,  , поэтому мы можем написать
, поэтому мы можем написать

куда  это инженерия напряжение. Это уравнение часто записывают в альтернативных обозначениях как
это инженерия напряжение. Это уравнение часто записывают в альтернативных обозначениях как

Вышеприведенное уравнение предназначено для настоящий стресс (отношение силы удлинения к деформированному сечению). Для инженерное напряжение уравнение:

Для небольших деформаций  у нас будет:
у нас будет:

Таким образом, эквивалент Модуль для младших неогуковского твердого тела при одноосном растяжении  , что соответствует линейной упругости (
, что соответствует линейной упругости ( с
с  на несжимаемость).
на несжимаемость).
Равноосное удлинение
Сжимаемый материал в стиле нео-Гук

Истинное напряжение как функция двухосного растяжения, предсказанное сжимаемым материалом неогуковского периода для различных значений

. Свойства материала типичны для
натуральная резина.
В случае равноосного удлинения

Следовательно,
![{ begin {align} sigma _ {{11}} & = 2C_ {1} left [{ cfrac { lambda ^ {2}} {J ^ {{5/3}}}}} - { cfrac {1} {3J}} left (2 lambda ^ {2} + { cfrac {J ^ {2}} { lambda ^ {4}}} right) right] + 2D_ {1} (J -1) & = sigma _ {{22}} sigma _ {{33}} & = 2C_ {1} left [{ cfrac {J ^ {{1/3}}}} { лямбда ^ {4}}} - { cfrac {1} {3J}} left (2 lambda ^ {2} + { cfrac {J ^ {2}} { lambda ^ {4}}} right ) right] + 2D_ {1} (J-1) end {align}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad7fd4f530a9b5f2bc1a10096975392ba12ae0be)
Различия в напряжении

Если материал находится в состоянии плоского напряжения, тогда  и у нас есть
и у нас есть

У нас также есть связь между  и
и  :
:
![2C_ {1} left [{ cfrac { lambda ^ {2}} {J ^ {{5/3}}}} - { cfrac {1} {3J}} left (2 lambda ^ {2 } + { cfrac {J ^ {2}} { lambda ^ {4}}} right) right] + 2D_ {1} (J-1) = { cfrac {2C_ {1}} {J ^ {{5/3}}}} left ( lambda ^ {2} - { cfrac {J ^ {2}} { lambda ^ {4}}} right)](https://wikimedia.org/api/rest_v1/media/math/render/svg/650a293ebe9af900c3775c1f566a4214c33edc38)
или же,

Это уравнение можно решить для  используя метод Ньютона.
используя метод Ньютона.
Несжимаемый материал в стиле нео-Гук
Для несжимаемого материала  а разности главных напряжений Коши принимают вид
а разности главных напряжений Коши принимают вид

В условиях плоского напряжения имеем

Чистая дилатация
В случае чистой дилатации

Следовательно, главные напряжения Коши для сжимаемого неогуковского материала определяются выражением

Если материал несжимаемый, то  а главные напряжения могут быть произвольными.
а главные напряжения могут быть произвольными.
На рисунках ниже показано, что для достижения большого трехосного растяжения или сжатия необходимы чрезвычайно высокие напряжения. Эквивалентно относительно небольшие состояния трехосного растяжения могут вызывать очень высокие напряжения в резиноподобном материале. Величина напряжения весьма чувствительна к модулю объемной упругости, но не к модулю сдвига.
 Истинное напряжение как функция равнотриаксиального растяжения, предсказанное сжимаемым материалом неогуковского периода для различных значений  . Свойства материала типичны для натуральная резина. |  Истинное напряжение как функция J, предсказанное сжимаемым материалом неогуковского периода для различных значений  . Свойства материала типичны для натуральная резина. |
Простой сдвиг
В случае простой сдвиг градиент деформации по компонентам относительно базисного значения имеет вид [1]

куда  деформация сдвига. Следовательно, левый тензор деформации Коши - Грина имеет вид
деформация сдвига. Следовательно, левый тензор деформации Коши - Грина имеет вид

Сжимаемый материал в стиле нео-Гук
В этом случае  . Следовательно,
. Следовательно,  . Сейчас же,
. Сейчас же,

Следовательно, напряжение Коши определяется выражением

Несжимаемый материал в стиле нео-Гук
Используя соотношение для напряжения Коши для несжимаемого неогуковского материала, получаем

Таким образом, неогуковское твердое тело показывает линейную зависимость касательных напряжений от деформации сдвига и квадратичную зависимость разности нормальных напряжений от деформации сдвига. Выражения для напряжения Коши для сжимаемого и несжимаемого неогуковского материала при простом сдвиге представляют одну и ту же величину и обеспечивают средство определения неизвестного давления.  .
.
Рекомендации
- ^ а б c Огден, Р. У. (26 апреля 2013 г.). Нелинейные упругие деформации. Курьерская корпорация. ISBN 978-0-486-31871-4.
- ^ Гент, А. Н., изд., 2001, Инжиниринг с резиной, Карл Хансер Верлаг, Мюнхен.
- ^ Пенс, Т. Дж., И Гоу, К. (2015). О сжимаемых версиях несжимаемого материала нео-Гука. Математика и механика твердого тела, 20(2), 157–182. [1]
Смотрите также




























![{ displaystyle { boldsymbol { sigma}} = { cfrac {2} {J}} left [{ cfrac {1} {J ^ {2/3}}} left ({ cfrac { partial {W}} { partial { bar {I}} _ {1}}} + { bar {I}} _ {1} ~ { cfrac { partial {W}} { partial { bar { I}} _ {2}}} right) { boldsymbol {B}} - { cfrac {1} {J ^ {4/3}}} ~ { cfrac { partial {W}} { partial { bar {I}} _ {2}}} ~ { boldsymbol {B}} cdot { boldsymbol {B}} right] + left [{ cfrac { partial {W}} { partial J}} - { cfrac {2} {3J}} left ({ bar {I}} _ {1} ~ { cfrac { partial {W}} { partial { bar {I}} _ {1}}} + 2 ~ { bar {I}} _ {2} ~ { cfrac { partial {W}} { partial { bar {I}} _ {2}}} right) справа] ~ { boldsymbol {I}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a02006f31ec08f5ff11d32479fcc80ae15ffb0ea)


![{ displaystyle { boldsymbol { sigma}} = { cfrac {2} {J}} left [{ cfrac {1} {J ^ {2/3}}} ~ C_ {1} ~ { boldsymbol {B}} right] + left [2D_ {1} (J-1) - { cfrac {2} {3J}} ~ C_ {1} { bar {I}} _ {1} right] { boldsymbol {I}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/120f858b142ddd9ee4ad00a67d5fb3bb9b99c1ae)
![{ displaystyle { boldsymbol { sigma}} = { cfrac {2} {J}} left [{ cfrac {1} {J ^ {2/3}}} ~ C_ {1} ~ { boldsymbol {B}} right] + left [2D_ {1} (J-1) - { cfrac {2C_ {1}} {J}} - { cfrac {2} {3J}} ~ C_ {1} { bar {I}} _ {1} right] { boldsymbol {I}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83d1614008549ca9e50b92d17563b2f0c2bcf4ac)

![{ displaystyle { boldsymbol { sigma}} = { cfrac {2C_ {1}} {J}} left [{ bar { boldsymbol {B}}} - { tfrac {1} {3}} { bar {I}} _ {1} { boldsymbol {I}} right] + 2D_ {1} (J-1) { boldsymbol {I}} = { cfrac {2C_ {1}} {J }} operatorname {dev} ({ bar { boldsymbol {B}}}) + 2D_ {1} (J-1) { boldsymbol {I}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b584cedbf95ffa49a8e0ced00a2756041e5cc65)
![{ displaystyle { boldsymbol { sigma}} = { cfrac {2C_ {1}} {J}} left [{ bar { boldsymbol {B}}} - { tfrac {1} {3}} { bar {I}} _ {1} { boldsymbol {I}} - { boldsymbol {I}} right] + 2D_ {1} (J-1) { boldsymbol {I}} = { cfrac {2C_ {1}} {J}} left [ operatorname {dev} ({ bar { boldsymbol {B}}}) - { boldsymbol {I}} right] + 2D_ {1} (J- 1) { boldsymbol {I}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/336115e7026192205dd2f146f41c09e65b22caf8)






![sigma _ {{i}} = 2C_ {1} J ^ {{- 5/3}} left [ lambda _ {i} ^ {2} - { cfrac {I_ {1}} {3}} right] + 2D_ {1} (J-1) ~; ~~ i = 1,2,3](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1e8671c7cc3313e7f11cd4b42d7d466d7b4bf69)


![W = C_ {1} ({ bar {I}} _ {1} -3) + D_ {1} (J-1) ^ {2} = C_ {1} left [J ^ {{- 2 / 3}} ( lambda _ {1} ^ {2} + lambda _ {2} ^ {2} + lambda _ {3} ^ {2}) - 3 right] + D_ {1} (J- 1) ^ {2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3080a7a8adbd13388160411dcb3347e301d86d0)
![lambda _ {i} { frac { partial W} { partial lambda _ {i}}} = C_ {1} left [- { frac {2} {3}} J ^ {{- 5 / 3}} lambda _ {i} { frac { partial J} { partial lambda _ {i}}} ( lambda _ {1} ^ {2} + lambda _ {2} ^ {2 } + lambda _ {3} ^ {2}) + 2J ^ {{- 2/3}} lambda _ {i} ^ {2} right] + 2D_ {1} (J-1) lambda _ {i} { frac { partial J} { partial lambda _ {i}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87611cb53239ecb742121e0e9535183c69fc69b5)


![{ begin {align} lambda _ {i} { frac { partial W} { partial lambda _ {i}}} & = C_ {1} left [- { frac {2} {3} } J ^ {{- 2/3}} ( lambda _ {1} ^ {2} + lambda _ {2} ^ {2} + lambda _ {3} ^ {2}) + 2J ^ {{ -2/3}} lambda _ {i} ^ {2} right] + 2D_ {1} J (J-1) & = 2C_ {1} J ^ {{- 2/3}} left [- { frac {1} {3}} ( lambda _ {1} ^ {2} + lambda _ {2} ^ {2} + lambda _ {3} ^ {2}) + lambda _ {i} ^ {2} right] + 2D_ {1} J (J-1) end {выравнивается}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c326c274fc12ae0344245cd5c390a34b06a6dd74)
![sigma _ {i} = 2C_ {1} J ^ {{- 5/3}} left [ lambda _ {i} ^ {2} - { cfrac {I_ {1}} {3}} right ] + 2D_ {1} (J-1)](https://wikimedia.org/api/rest_v1/media/math/render/svg/ceaecb06369b0b2869a0bb4180f929d238ef28c9)




























![{ begin {align} sigma _ {{11}} & = 2C_ {1} left [{ cfrac { lambda ^ {2}} {J ^ {{5/3}}}}} - { cfrac {1} {3J}} left (2 lambda ^ {2} + { cfrac {J ^ {2}} { lambda ^ {4}}} right) right] + 2D_ {1} (J -1) & = sigma _ {{22}} sigma _ {{33}} & = 2C_ {1} left [{ cfrac {J ^ {{1/3}}}} { лямбда ^ {4}}} - { cfrac {1} {3J}} left (2 lambda ^ {2} + { cfrac {J ^ {2}} { lambda ^ {4}}} right ) right] + 2D_ {1} (J-1) end {align}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad7fd4f530a9b5f2bc1a10096975392ba12ae0be)



![2C_ {1} left [{ cfrac { lambda ^ {2}} {J ^ {{5/3}}}} - { cfrac {1} {3J}} left (2 lambda ^ {2 } + { cfrac {J ^ {2}} { lambda ^ {4}}} right) right] + 2D_ {1} (J-1) = { cfrac {2C_ {1}} {J ^ {{5/3}}}} left ( lambda ^ {2} - { cfrac {J ^ {2}} { lambda ^ {4}}} right)](https://wikimedia.org/api/rest_v1/media/math/render/svg/650a293ebe9af900c3775c1f566a4214c33edc38)













