WikiDer > Поверхностное натяжение
Эта статья требует внимания специалиста по физике. (Июнь 2019) |
Эта статья может потребоваться переписан соответствовать требованиям Википедии стандарты качества. (Июнь 2019) |

| Часть серии по | ||||
| Механика сплошной среды | ||||
|---|---|---|---|---|
Законы
| ||||
Поверхностное натяжение это тенденция жидкость поверхности сжать до минимума площадь поверхности возможный. Поверхностное натяжение позволяет насекомым (например, водомеры), обычно плотнее воды, чтобы плавать и скользить по поверхности воды.
На границах раздела жидкость – воздух поверхностное натяжение возникает в результате большего притяжения молекул жидкости друг к другу (из-за сплоченность), чем молекулы в воздухе (из-за адгезия).
Здесь задействованы два основных механизма. Один из них - внутренняя сила, действующая на молекулы поверхности, заставляющая жидкость сжиматься.[1][2] Во-вторых, это касательная сила, параллельная поверхности жидкости.[2] В результате жидкость ведет себя так, как если бы ее поверхность была покрыта растянутой эластичной мембраной.
Из-за относительно сильного притяжения молекул воды друг к другу через сеть водородных связей вода имеет более высокое поверхностное натяжение (72,8 миллиньютон (мН) на метр при 20 ° C), чем у большинства других жидкостей. Поверхностное натяжение - важный фактор в явлении капиллярность.
Поверхностное натяжение имеет измерение из сила на единицу длина, или из энергия на единицу площадь. Эти два эквивалента, но когда речь идет об энергии на единицу площади, обычно используется термин поверхностная энергия, который является более общим термином в том смысле, что он также применяется к твердые вещества.
В материаловедение, поверхностное натяжение используется либо для поверхностное напряжение или же поверхностная энергия.
Причины
Из-за силы сцепления молекула равномерно тянется во всех направлениях соседними молекулами жидкости, в результате чего результирующая сила равна нулю. Молекулы на поверхности не имеют одно и тоже молекулы со всех сторон и поэтому притягиваются внутрь. Это создает некоторые внутреннее давление и заставляет жидкие поверхности сжиматься до минимальной площади.[1]
Также существует напряжение, параллельное поверхности на границе раздела жидкость-воздух, которое будет противостоять внешней силе из-за когезионной природы молекул воды.[1][2]
Силы притяжения, действующие между молекулами одного типа, называются силами сцепления, а силы, действующие между молекулами разных типов, - силами сцепления. Баланс между сцеплением жидкости и ее адгезией к материалу контейнера определяет степень смачивание, то угол контакта и форма мениск. Когда когезия доминирует (в частности, энергия адгезии составляет менее половины энергии сцепления), смачивание низкое и мениск выпуклый у вертикальной стенки (как для ртути в стеклянном сосуде). С другой стороны, когда адгезия преобладает (энергия адгезии превышает половину энергии сцепления), смачивание высокое, и аналогичный мениск вогнутый (как в воде в стакане).
Поверхностное натяжение отвечает за форму жидких капель. Хотя капельки воды легко деформируются, они имеют тенденцию принимать сферическую форму из-за дисбаланса сил сцепления поверхностного слоя. В отсутствие других сил капли практически всех жидкостей были бы приблизительно сферическими. Сферическая форма сводит к минимуму необходимое «натяжение стенки» поверхностного слоя в соответствии с Закон Лапласа.

Другой способ увидеть поверхностное натяжение - это энергия. Молекула в контакте с соседом находится в более низком энергетическом состоянии, чем если бы она была одна. Внутренние молекулы имеют столько соседей, сколько возможно, но граничные молекулы не имеют соседей (по сравнению с внутренними молекулами) и, следовательно, имеют более высокую энергию. Чтобы жидкость минимизировала свое энергетическое состояние, необходимо минимизировать количество граничных молекул с более высокой энергией. Минимальное количество граничных молекул приводит к минимальной площади поверхности.[3]В результате минимизации площади поверхности поверхность примет максимально гладкую форму (математическое доказательство того, что «гладкие» формы минимизируют площадь поверхности, зависит от использования Уравнение Эйлера – Лагранжа.). Поскольку любая кривизна формы поверхности приводит к увеличению площади, в результате также будет увеличиваться энергия.
Эффекты поверхностного натяжения
Вода
С обычной водой можно увидеть несколько эффектов поверхностного натяжения:
- Бусинки дождевой воды на восковой поверхности, например на листе. Вода придерживается слабо воском и сильно к себе, поэтому вода собирается в капли. Поверхностное натяжение придает им форму, близкую к сферической, потому что сфера имеет наименьший возможный размер. отношение площади поверхности к объему.
- Формирование капли возникает, когда масса жидкости растягивается. На анимации (ниже) показано, как вода, приставшая к крану, набирает массу, пока не растянется до точки, в которой поверхностное натяжение больше не может удерживать каплю, связанную со смесителем. Затем он отделяется, и поверхностное натяжение превращает каплю в сферу. Если бы из крана текла струя воды, во время падения струя разбилась бы на капли. Гравитация растягивает ручей, а затем поверхностное натяжение сжимает его в сферы.[4]
- Плавание объектов, более плотных, чем вода, происходит, когда объект не смачивается, а его вес достаточно мал, чтобы выдерживать силы, возникающие из-за поверхностного натяжения.[3] Например, водомеры Используйте поверхностное натяжение для ходьбы по поверхности пруда следующим образом. Несмачиваемость ноги водомера означает, что нет притяжения между молекулами ноги и молекулами воды, поэтому, когда нога толкает воду, поверхностное натяжение воды пытается восстановить свою плоскостность только из-за ее деформации из-за нога. Такое поведение воды толкает водомер вверх, чтобы он мог стоять на поверхности воды, пока его масса достаточно мала, чтобы вода могла его поддерживать. Поверхность воды ведет себя как эластичная пленка: ноги насекомого вызывают вмятины на поверхности воды, увеличивая ее площадь.[5] и тенденция к минимизации кривизны поверхности (т.е. площади) воды подталкивает ноги насекомого вверх.
- Разделение масла и воды (в данном случае воды и жидкого воска) вызвано натяжением поверхности между разнородными жидкостями. Этот тип поверхностного натяжения называется «межфазным натяжением», но его химический состав тот же.
- Слезы вина образование капель и ручейков на стенке стакана с алкогольным напитком. Его причина - сложное взаимодействие между различными поверхностными натяжениями воды и этиловый спирт; это вызвано комбинацией модификации поверхностного натяжения воды за счет этиловый спирт вместе с этанолом испаряющийся быстрее воды.
С. Водомеры оставаться на поверхности жидкости из-за поверхностного натяжения
Д. Лавовая лампа при взаимодействии разнородных жидкостей: воды и жидкого воска
Э. Фотография с изображением "слезы вина"явление.
Поверхностно-активные вещества
Поверхностное натяжение проявляется в других общих явлениях, особенно когда поверхностно-активные вещества используются для его уменьшения:
- Мыльные пузыри имеют очень большую площадь поверхности при очень небольшой массе. Пузыри в чистой воде нестабильны. Однако добавление поверхностно-активных веществ может иметь стабилизирующий эффект на пузырьки (см. Эффект Марангони). Обратите внимание, что поверхностно-активные вещества фактически снижают поверхностное натяжение воды в три или более раз.
- Эмульсии представляют собой тип коллоида, в котором поверхностное натяжение играет роль. Крошечные фрагменты нефти, взвешенные в чистой воде, спонтанно собираются в гораздо более крупные массы. Но присутствие поверхностно-активного вещества обеспечивает снижение поверхностного натяжения, что обеспечивает стабильность мельчайших капелек масла в объеме воды (или наоборот).
Физика
Физические единицы
Поверхностное натяжение, обозначенное символом γ (альтернативно σ или же Т), измеряется в сила на длина единицы. Его SI единица ньютон за метр, но cgs единица Дайн на сантиметр также используется. Например,[6]
Рост площади поверхности
Поверхностное натяжение можно определить как силу или энергию.
С точки зрения силы
Поверхностное натяжение γ жидкости - сила на единицу длины. На рисунке справа прямоугольная рамка состоит из трех неподвижных сторон (черные), образующих U-образную форму, и четвертой подвижной стороны (синей), которая может сдвигаться вправо. Поверхностное натяжение потянет синюю полосу влево; сила F необходимая для удержания подвижной стороны пропорциональна длине L неподвижной стороны. Таким образом, соотношение F/L зависит только от внутренних свойств жидкости (состава, температуры и т. д.), а не от ее геометрии. Например, если рамка имела более сложную форму, соотношение F/L, с L длина подвижной стороны и F сила, необходимая для предотвращения скольжения, одинакова для всех форм. Поэтому мы определяем поверхностное натяжение как
Причина 1/2 состоит в том, что пленка имеет две стороны (две поверхности), каждая из которых вносит равный вклад в силу; поэтому сила, вносимая одной стороной, равна γL = F/2.
С точки зрения энергии
Поверхностное натяжение γ жидкости - это отношение изменения энергии жидкости к изменению площади поверхности жидкости (которое привело к изменению энергии). Это можно легко соотнести с предыдущим определением с точки зрения силы:[7] если F сила, необходимая, чтобы остановить сторону от начало скользить, то это также сила, которая удерживала бы сторону в состоянии скольжение с постоянной скоростью (по второму закону Ньютона). Но если сторона движется вправо (в направлении приложения силы), то площадь поверхности растянутой жидкости увеличивается, в то время как приложенная сила выполняет работу с жидкостью. Это означает, что увеличение площади поверхности увеличивает энергию пленки. Работа, проделанная силой F в движении бок о бок ΔИкс является W = FΔИкс; при этом общая площадь пленки увеличивается на ΔА = 2LΔИкс (коэффициент 2 здесь, потому что жидкость имеет две стороны, две поверхности). Таким образом, умножая числитель и знаменатель γ = 1/2F/L к ΔИкс, мы получили
- .
Эта работа W есть, по обычные аргументы, интерпретируется как запасенная как потенциальная энергия. Следовательно, поверхностное натяжение можно также измерить в системе СИ в джоулях на квадратный метр и в cgs система как эрг на см2. С механические системы пытаются найти состояние минимальной потенциальной энергиисвободная капля жидкости естественным образом принимает сферическую форму, которая имеет минимальную площадь поверхности для данного объема. Эквивалентность измерения энергии на единицу площади силе на единицу длины может быть доказана следующим образом: размерный анализ.[8]
Кривизна поверхности и давление

Если никакая сила не действует перпендикулярно натянутой поверхности, поверхность должна оставаться плоской. Но если давление на одной стороне поверхности отличается от давления на другой стороне, разность давлений, умноженная на площадь поверхности, дает нормальную силу. Чтобы силы поверхностного натяжения нейтрализовали силу давления, поверхность должна быть искривленной. На диаграмме показано, как кривизна поверхности крошечного участка поверхности приводит к суммарной составляющей сил поверхностного натяжения, действующих перпендикулярно центру пятна. Когда все силы уравновешены, результирующее уравнение известно как Уравнение Юнга – Лапласа:[9]
куда:
- Δп перепад давления, известный как Давление Лапласа.[10]
- γ поверхностное натяжение.
- рИкс и ру находятся радиусы кривизны в каждой из осей, параллельных поверхности.
Количество в скобках справа на самом деле (в два раза) больше средняя кривизна поверхности (в зависимости от нормализации) .Решение этого уравнения определяет форму водяных капель, луж, менисков, мыльных пузырей и все другие формы, определяемые поверхностным натяжением (например, форму отпечатков, которые ступни водомета делают на В таблице ниже показано, как внутреннее давление капли воды увеличивается с уменьшением радиуса. Для не очень маленьких капель эффект незначительный, но разница в давлении становится огромной, когда размер капель приближается к размеру молекулы. (В пределах одной молекулы концепция теряет смысл.)
| Радиус капли | 1 мм | 0,1 мм | 1 мкм | 10 нм |
|---|---|---|---|---|
| Δп (банкомат) | 0.0014 | 0.0144 | 1.436 | 143.6 |
Плавающие объекты
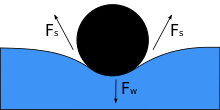
Когда объект помещается в жидкость, его вес Fш сдавливает поверхность, и если поверхностное натяжение и направленная вниз сила становятся равными, это уравновешивается силами поверхностного натяжения с обеих сторон Fs, каждая из которых параллельна поверхности воды в точках контакта с объектом. Обратите внимание, что небольшое движение тела может привести к тому, что объект утонет. По мере уменьшения угла контакта поверхностное натяжение уменьшается. Горизонтальные компоненты двух Fs стрелки указывают в противоположных направлениях, поэтому они компенсируют друг друга, но вертикальные компоненты указывают в одном направлении и, следовательно, складываются[3] сбалансировать Fш. Чтобы это произошло, поверхность объекта не должна быть смачиваемой, а его вес должен быть достаточно низким, чтобы его могло поддерживать поверхностное натяжение.
Жидкая поверхность
Чтобы найти форму минимальная поверхность ограниченный рамкой произвольной формы с использованием строго математических средств, может оказаться сложной задачей. Тем не менее, если сделать каркас из проволоки и окунуть его в мыльный раствор, в полученной мыльной пленке в течение нескольких секунд появится локально минимальная поверхность.[8][11]
Причина этого в том, что разность давлений на границе раздела жидкостей пропорциональна средняя кривизна, как видно на Уравнение Юнга – Лапласа. Для открытой мыльной пленки перепад давления равен нулю, следовательно, средняя кривизна равна нулю, а минимальные поверхности обладают свойством нулевой средней кривизны.
Углы контакта
Поверхность любой жидкости - это граница между этой жидкостью и какой-либо другой средой.[примечание 1] Например, верхняя поверхность пруда - это поверхность раздела между водой пруда и воздухом. Таким образом, поверхностное натяжение - это свойство не только жидкости, а свойство границы раздела жидкости с другой средой. Если жидкость находится в контейнере, то помимо поверхности раздела жидкость / воздух на его верхней поверхности существует также поверхность раздела между жидкостью и стенками контейнера. Поверхностное натяжение между жидкостью и воздухом обычно отличается (больше) от его поверхностного натяжения со стенками емкости. И там, где две поверхности встречаются, их геометрия должна быть такой, чтобы все силы уравновешивались.[8][9]
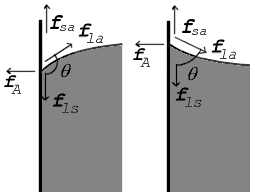
Где две поверхности встречаются, они образуют угол контакта, θ, который представляет собой угол касательной к поверхности с твердой поверхностью. Обратите внимание, что угол измеряется через жидкость, как показано на схемах выше. На диаграмме справа показаны два примера. Силы натяжения показаны для границы раздела жидкость-воздух, границы раздела жидкость-твердое тело и границы раздела твердое тело-воздух. Пример слева показывает разницу между поверхностным натяжением жидкость – твердое тело и твердое тело – воздух, γls − γса, меньше поверхностного натяжения жидкость – воздух, γля, но тем не менее положительный, то есть
На диаграмме вертикальные и горизонтальные силы должны компенсироваться точно в точке контакта, известной как равновесие. Горизонтальная составляющая жля отменяется силой сцепления, жА.[8]
Однако более показательный баланс сил находится в вертикальном направлении. Вертикальная составляющая жля должен точно компенсировать разность сил вдоль твердой поверхности, жls − жса.[8]
| Жидкость | Твердый | Угол контакта | |||
|---|---|---|---|---|---|
| воды |
| 0° | |||
| этиловый спирт | |||||
| диэтиловый эфир | |||||
| четыреххлористый углерод | |||||
| глицерин | |||||
| уксусная кислота | |||||
| воды | парафиновая свеча | 107° | |||
| серебро | 90° | ||||
| йодистый метил | натриево-известковое стекло | 29° | |||
| свинцовое стекло | 30° | ||||
| плавленый кварц | 33° | ||||
| Меркурий | натриево-известковое стекло | 140° | |||
| Некоторые краевые углы между жидкостью и твердым телом[8] | |||||
Поскольку силы прямо пропорциональны их поверхностному натяжению, мы также имеем:[9]
куда
- γls - поверхностное натяжение жидкость – твердое тело,
- γля - поверхностное натяжение жидкость – воздух,
- γса - поверхностное натяжение твердого тела и воздуха,
- θ - угол контакта, где вогнутая мениск имеет угол контакта менее 90 °, а выпуклый мениск имеет угол контакта более 90 °.[8]
Это означает, что хотя разница между поверхностным натяжением жидкость – твердое тело и твердое тело – воздух, γls − γса, трудно измерить напрямую, его можно определить по поверхностному натяжению жидкость – воздух, γля, а равновесный контактный угол θ, который является функцией легко измеряемых углов смачивания и удаления (см. основную статью угол контакта).
Такая же взаимосвязь существует на диаграмме справа. Но в этом случае мы видим, что, поскольку угол смачивания меньше 90 °, разница поверхностного натяжения жидкость-твердое тело / твердое тело-воздух должна быть отрицательной:
Специальные углы контакта
Обратите внимание, что в частном случае границы раздела вода-серебро, когда угол смачивания равен 90 °, разница поверхностного натяжения жидкость-твердое тело / твердое тело-воздух точно равна нулю.
Другой особый случай - угол контакта точно 180 °. Вода со специально подготовленной Тефлон подходит к этому.[9] Угол смачивания 180 ° возникает, когда поверхностное натяжение жидкость – твердое тело в точности равно поверхностному натяжению жидкость – воздух.
Методы измерения
Поскольку поверхностное натяжение проявляется в различных эффектах, он предлагает несколько способов его измерения. Выбор оптимального метода зависит от природы измеряемой жидкости, условий измерения ее натяжения и устойчивости ее поверхности при ее деформации. Инструмент, измеряющий поверхностное натяжение, называется тензиометр.
- Метод кольца Дю Нюи: Традиционный метод измерения поверхностного или межфазного натяжения. Смачивающие свойства поверхности или границы раздела мало влияют на этот метод измерения. Измеряется максимальное усилие, прилагаемое к кольцу поверхностью.[12]
- Метод пластины Вильгельми: Универсальный метод, особенно подходящий для проверки поверхностного натяжения в течение длительного времени. К весам прикрепляют вертикальную пластину известного периметра и измеряют силу, обусловленную смачиванием.[13]
- Метод вращающейся капли: Этот метод идеально подходит для измерения низкого межфазного натяжения. Диаметр капли в тяжелой фазе измеряется при вращении обеих.
- Подвесной метод падения: Поверхностное и межфазное натяжение можно измерить этим методом даже при повышенных температурах и давлениях. Геометрия капли анализируется оптически. Для подвесных капель максимальный диаметр и соотношение между этим параметром и диаметром на расстоянии максимального диаметра от вершины капли использовались для оценки параметров размера и формы с целью определения поверхностного натяжения.[13]
- Метод пузырькового давления (Метод Джегера): метод измерения для определения поверхностного натяжения при коротком поверхностном возрасте. Измеряется максимальное давление каждого пузырька.
- Метод объема капли: метод определения межфазного натяжения как функции возраста границы раздела фаз. Жидкость одной плотности перекачивается во вторую жидкость другой плотности, и измеряется время между появлением капель.[14]
- Метод капиллярного подъема: конец капилляра погружается в раствор. Высота, на которой раствор достигает внутри капилляра, связана с поверхностным натяжением уравнением обсуждается ниже.[15]
 Поверхностное натяжение можно измерить методом подвесной капли на гониометр.
Поверхностное натяжение можно измерить методом подвесной капли на гониометр. - Сталагмометрический метод: Метод взвешивания и считывания капель жидкости.
- Метод сеансового сброса: Метод определения поверхностного натяжения и плотность поместив каплю на подложку и измерив угол контакта (видеть Техника Sessile drop).[16]
- Метод Дю Нуи – Паддея: Уменьшенная версия метода Дю Нюи использует металлическую иглу малого диаметра вместо кольца в сочетании с высокочувствительными микровесами для регистрации максимального усилия. Преимущество этого метода заключается в том, что очень маленькие объемы образца (до нескольких десятков микролитров) могут быть измерены с очень высокой точностью без необходимости корректировки плавучесть (для иглы, а точнее стержня, правильной геометрии). Кроме того, измерение может быть выполнено очень быстро, минимум за 20 секунд.
- Частота колебаний левитирующих капель: собственная частота колебательных колебаний магнитно-левитирующих капель использовалась для измерения поверхностного натяжения сверхтекучей жидкости. 4Он. Это значение оценивается в 0,375 дин / см при Т = 0 К.[17]
- Резонансные колебания сферических и полусферических жидких капель: метод основан на измерении резонансной частоты сферических и полусферических висячих капель, колеблющихся под действием модулированного электрического поля. Поверхностное натяжение и вязкость можно оценить по полученным резонансным кривым.[18][19][20]
Последствия
Жидкость в вертикальной трубке
Старый стиль Меркурий барометр состоит из вертикальной стеклянной трубки диаметром около 1 см, частично заполненной ртутью, и с вакуумом (называемым Торричелливакуум) в незаполненном объеме (см. диаграмму справа). Обратите внимание, что уровень ртути в центре трубки выше, чем по краям, что делает верхнюю поверхность ртути куполообразной. Центр масс всего столбика ртути был бы немного ниже, если бы верхняя поверхность ртути была бы плоской по всему поперечному сечению трубки. Но куполообразный верх дает немного меньшую площадь поверхности всей массе ртути. И снова два эффекта объединяются, чтобы минимизировать общую потенциальную энергию. Такая форма поверхности известна как выпуклый мениск.
Мы рассматриваем площадь поверхности всей массы ртути, включая ту часть поверхности, которая контактирует со стеклом, потому что ртуть вообще не прилипает к стеклу. Таким образом, поверхностное натяжение ртути действует по всей площади ее поверхности, в том числе там, где она контактирует со стеклом. Если бы вместо стекла трубку сделали из меди, ситуация была бы совсем другой. Ртуть агрессивно сцепляется с медью. Таким образом, в медной трубке уровень ртути в центре трубки будет ниже, чем на краях (то есть это будет вогнутый мениск). В ситуации, когда жидкость прилипает к стенкам своего контейнера, мы считаем, что часть площади поверхности жидкости, которая контактирует с контейнером, имеет отрицательный поверхностное натяжение. Затем жидкость работает, чтобы максимизировать площадь контактной поверхности. Таким образом, в этом случае увеличение площади контакта с контейнером уменьшает, а не увеличивает потенциальную энергию. Этого уменьшения достаточно, чтобы компенсировать повышенную потенциальную энергию, связанную с подъемом жидкости возле стенок контейнера.
Если трубка достаточно узкая и адгезия жидкости к ее стенкам достаточно сильна, поверхностное натяжение может втягивать жидкость вверх по трубке в результате явления, известного как капиллярное действие. Высота, на которую поднимается колонна, определяется выражением Закон Журина:[8]
куда
- час высота подъема жидкости,
- γля - поверхностное натяжение жидкость – воздух,
- ρ плотность жидкости,
- р - радиус капилляра,
- грамм ускорение свободного падения,
- θ - это угол контакта, описанный выше. Если θ больше 90 °, как и в случае с ртутью в стеклянном контейнере, жидкость будет подаваться, а не подниматься.
Лужи на поверхности
Залив ртутью на горизонтальный плоский лист стекла, получается лужа который имеет ощутимую толщину. Лужа будет расширяться только до такой степени, что ее толщина будет чуть меньше полсантиметра, и не тоньше. Опять же, это связано с действием сильного поверхностного натяжения ртути. Жидкая масса выравнивается, потому что это приводит как можно больше ртути к как можно более низкому уровню, но в то же время поверхностное натяжение сокращает общую площадь поверхности. Результатом компромисса является лужа почти фиксированной толщины.
Такую же демонстрацию поверхностного натяжения можно провести с водой, известковой водой или даже солевым раствором, но только на поверхности, сделанной из вещества, к которому вода не прилипает. Воск - такое вещество. Вода, налитая на гладкую плоскую горизонтальную восковую поверхность, скажем, на вощеный лист стекла, будет вести себя так же, как ртуть, налитая на стекло.
Толщина лужи жидкости на поверхности, угол смачивания которой составляет 180 °, определяется по формуле:[9]
куда
- час - глубина лужи в сантиметрах или метрах.
- γ представляет собой поверхностное натяжение жидкости в дин на сантиметр или в ньютонах на метр.
- грамм - ускорение свободного падения, равное 980 см / с.2 или 9,8 м / с2
- ρ плотность жидкости в граммах на кубический сантиметр или килограммах на кубический метр
На самом деле толщина луж будет немного меньше, чем предсказывается приведенной выше формулой, потому что очень немногие поверхности имеют угол контакта 180 ° с любой жидкостью. Когда угол контакта меньше 180 °, толщина определяется по формуле:[9]
Для ртути на стекле, γHg = 487 дин / см, ρHg = 13,5 г / см3 и θ = 140 °, что дает часHg = 0,36 см. Для воды на парафине при 25 ° C, γ = 72 дин / см, ρ = 1,0 г / см3, и θ = 107 °, что дает часЧАС2О = 0,44 см.
Формула также предсказывает, что когда угол смачивания равен 0 °, жидкость будет растекаться в виде микротонкого слоя по поверхности. Такая поверхность считается полностью смачиваемой жидкостью.
Распад струй на капли
В повседневной жизни все мы замечаем, что струя воды, выходящая из крана, распадается на капли, независимо от того, насколько плавно струя выходит из крана. Это связано с явлением, называемым Неустойчивость Плато – Рэлея.,[9] которое полностью является следствием поверхностного натяжения.
Объяснение этой нестабильности начинается с существования крошечных возмущений в потоке. Они всегда присутствуют, независимо от того, насколько плавный поток. Если возмущения разложить на синусоидальный компонентов, мы обнаруживаем, что некоторые компоненты со временем растут, а другие со временем распадаются. Среди тех, которые растут со временем, одни растут быстрее, чем другие. Растет или распадается компонент, и насколько быстро он растет, полностью зависит от его волнового числа (мера того, сколько пиков и впадин на сантиметр) и радиусов исходного цилиндрического потока.
Термодинамика
Термодинамические теории поверхностного натяжения
J.W. Гиббс разработал термодинамическую теорию капиллярности, основанную на идее поверхностей разрыва.[21] Гиббс рассмотрел случай, когда острая математическая поверхность помещается где-то внутри микроскопически нечеткой физической границы раздела двух однородных веществ. Понимая, что точный выбор местоположения поверхности был несколько произвольным, он оставил его гибким. Поскольку поверхность раздела находится в тепловом и химическом равновесии с веществами вокруг нее (имеющими температуру Т и химические потенциалы μя), Гиббс рассмотрел случай, когда поверхность может иметь избыточную энергию, избыточную энтропию и избыточные частицы, найдя естественную функцию свободной энергии в этом случае , количество, позднее названное большой потенциал и учитывая символ .
Учитывая данный подобъем содержащий поверхность разрыва, объем делится математической поверхностью на две части A и B, с объемами и , с точно. Теперь, если бы две части A и B были однородными жидкостями (с давлением , ) и оставался идеально однородным вплоть до математической границы, без каких-либо поверхностных эффектов, общий великий потенциал этого объема был бы просто . Представляющие интерес поверхностные эффекты являются модификацией этого, и все они могут быть собраны в член свободной энергии поверхности таким образом, общий великий потенциал тома становится:
Для достаточно макроскопических и слегка изогнутых поверхностей свободная энергия поверхности должна быть просто пропорциональна площади поверхности:[21][22]
для поверхностного натяжения и площадь поверхности .
Как указано выше, это подразумевает механическую работу, необходимую для увеличения площади поверхности. А является dW = γ dAпри условии, что объемы с каждой стороны не меняются. Термодинамика требует, чтобы для систем, поддерживаемых при постоянном химическом потенциале и температуре, все спонтанные изменения состояния сопровождались уменьшением этой свободной энергии. , то есть увеличение полной энтропии с учетом возможного движения энергии и частиц с поверхности в окружающие жидкости. Отсюда легко понять, почему уменьшение площади поверхности массы жидкости всегда спонтанныйпри условии, что это не связано с другими изменениями энергии. Отсюда следует, что для увеличения площади поверхности необходимо добавить определенное количество энергии.
Гиббс и другие ученые боролись с произволом в точном микроскопическом расположении поверхности.[23] Для микроскопических поверхностей с очень малой кривизной неверно предполагать, что поверхностное натяжение не зависит от размера, и такие темы, как Длина Толмана вступают в игру. Для поверхности макроскопических размеров (и плоских поверхностей) размещение поверхности не оказывает значительного влияния на γ однако он имеет очень сильное влияние на значения поверхностной энтропии, поверхностной избыточной плотности массы и поверхностной внутренней энергии,[21]:237 которые являются частными производными функции поверхностного натяжения .
Гиббс подчеркнул, что для твердых тел свободная энергия поверхности может полностью отличаться от поверхностного напряжения (то, что он назвал поверхностным натяжением):[21]:315 свободная энергия поверхности - это работа, необходимая для форма поверхности, а поверхностное напряжение - это работа, необходимая для протяжение поверхность. В случае границы раздела двух жидкостей нет различия между формованием и растяжением, потому что жидкости и поверхность полностью восстанавливают свою природу, когда поверхность растягивается. Для твердого тела растяжение поверхности, даже упругое, приводит к фундаментальному изменению поверхности. Кроме того, поверхностное напряжение на твердом теле является направленной величиной (a тензор напряжений), а поверхностная энергия скалярна.
Пятнадцать лет спустя после Гиббса, J.D. van der Waals разработал теорию капиллярных эффектов, основанную на гипотезе непрерывного изменения плотности.[24] Он добавил к плотности энергии термин куда c - коэффициент капиллярности и ρ это плотность. Для многофазного равновесие, результаты подхода Ван-дер-Ваальса практически совпадают с формулами Гиббса, но для моделирования динамика Для фазовых переходов подход Ван-дер-Ваальса гораздо удобнее.[25][26] Энергия капиллярности Ван-дер-Ваальса сейчас широко используется в модели фазового поля многофазных потоков. Such terms are also discovered in the dynamics of non-equilibrium gases.[27]
Thermodynamics of bubbles
The pressure inside an ideal spherical bubble can be derived from thermodynamic free energy considerations.[22] The above free energy can be written as:
куда is the pressure difference between the inside (A) and outside (B) of the bubble, and is the bubble volume. In equilibrium, dΩ = 0, и так,
- .
For a spherical bubble, the volume and surface area are given simply by
и
Substituting these relations into the previous expression, we find
что эквивалентно Уравнение Юнга – Лапласа когда рИкс = ру.
Influence of temperature

Surface tension is dependent on temperature. For that reason, when a value is given for the surface tension of an interface, temperature must be explicitly stated. The general trend is that surface tension decreases with the increase of temperature, reaching a value of 0 at the критическая температура. Подробнее см. Правило Этвёша. There are only empirical equations to relate surface tension and temperature:
Здесь V is the molar volume of a substance, ТC это критическая температура и k is a constant valid for almost all substances.[12] Типичное значение k = 2.1×10−7 J K−1 моль−2⁄3.[12][29] For water one can further use V = 18 ml/mol and ТC = 647 K (374 °C).[30]
A variant on Eötvös is described by Ramay and Shields:[31]
where the temperature offset of 6 K provides the formula with a better fit to reality at lower temperatures.
- Guggenheim–Katayama:[28]
γ° is a constant for each liquid and п is an empirical factor, whose value is 11/9 for organic liquids. This equation was also proposed by ван дер Ваальс, who further proposed that γ° could be given by the expression
куда K2 is a universal constant for all liquids, and пC это критическое давление of the liquid (although later experiments found K2 to vary to some degree from one liquid to another).[28]
Both Guggenheim–Katayama and Eötvös take into account the fact that surface tension reaches 0 at the critical temperature, whereas Ramay and Shields fails to match reality at this endpoint.
Influence of solute concentration
Solutes can have different effects on surface tension depending on the nature of the surface and the solute:
- Little or no effect, for example сахар at water|air, most organic compounds at oil/air
- Increase surface tension, most неорганические соли at water|air
- Non-monotonic change, most inorganic acids at water|air
- Decrease surface tension progressively, as with most amphiphiles, e.g., спирты at water|air
- Decrease surface tension until certain critical concentration, and no effect afterwards: поверхностно-активные вещества that form micelles
What complicates the effect is that a solute can exist in a different concentration at the surface of a solvent than in its bulk. This difference varies from one solute–solvent combination to another.
Изотерма Гиббса states that:
- Γ is known as surface concentration, it represents excess of solute per unit area of the surface over what would be present if the bulk concentration prevailed all the way to the surface. It has units of mol/m2
- C is the concentration of the substance in the bulk solution.
- р это газовая постоянная и Т то температура
Certain assumptions are taken in its deduction, therefore Gibbs isotherm can only be applied to ideal (very dilute) solutions with two components.
Influence of particle size on vapor pressure
В Соотношение Клаузиуса – Клапейрона leads to another equation also attributed to Kelvin, as the Уравнение Кельвина. It explains why, because of surface tension, the давление газа for small droplets of liquid in suspension is greater than standard vapor pressure of that same liquid when the interface is flat. That is to say that when a liquid is forming small droplets, the equilibrium concentration of its vapor in its surroundings is greater. This arises because the pressure inside the droplet is greater than outside.[31]
- пv° is the standard vapor pressure for that liquid at that temperature and pressure.
- V is the molar volume.
- р это газовая постоянная
- рk is the Kelvin radius, the radius of the droplets.
The effect explains supersaturation of vapors. В отсутствие зарождение sites, tiny droplets must form before they can evolve into larger droplets. This requires a vapor pressure many times the vapor pressure at the фаза перехода точка.[31]
This equation is also used in катализатор chemistry to assess mesoporosity for solids.[32]
The effect can be viewed in terms of the average number of molecular neighbors of surface molecules (see diagram).
The table shows some calculated values of this effect for water at different drop sizes:
| п/п0 for water drops of different radii at STP[28] | ||||
|---|---|---|---|---|
| Droplet radius (nm) | 1000 | 100 | 10 | 1 |
| п/п0 | 1.001 | 1.011 | 1.114 | 2.95 |
The effect becomes clear for very small drop sizes, as a drop of 1 nm radius has about 100 molecules inside, which is a quantity small enough to require a квантовая механика анализ.
Surface tension of water and of seawater
The two most abundant liquids on the Earth are fresh воды и морская вода. This section gives correlations of reference data for the surface tension of both.
Surface tension of water
The surface tension of pure liquid water in contact with its vapor has been given by IAPWS[33] в качестве
where both Т and the critical temperature ТC = 647.096 K are expressed in кельвины. The region of validity the entire vapor–liquid saturation curve, from the triple point (0.01 °C) to the critical point. It also provides reasonable results when extrapolated to metastable (supercooled) conditions, down to at least −25 °C. This formulation was originally adopted by IAPWS in 1976 and was adjusted in 1994 to conform to the International Temperature Scale of 1990.
The uncertainty of this formulation is given over the full range of temperature by IAPWS.[33] For temperatures below 100 °C, the uncertainty is ±0.5%.
Surface tension of seawater
Nayar et al.[34] published reference data for the surface tension of seawater over the salinity range of 20 ≤ S ≤ 131 g/kg and a temperature range of 1 ≤ т ≤ 92 °C при атмосферном давлении. The range of temperature and salinity encompasses both the oceanographic range and the range of conditions encountered in thermal опреснение технологии. The uncertainty of the measurements varied from 0.18 to 0.37 mN/m with the average uncertainty being 0.22 mN/m.
Nayar et al. correlated the data with the following equation
куда γsw is the surface tension of seawater in mN/m, γш is the surface tension of water in mN/m, S is the reference salinity[35] in g/kg, and т is temperature in degrees Celsius. The average absolute percentage deviation between measurements and the correlation was 0.19% while the maximum deviation is 0.60%.
The International Association for the Properties of Water and Steam (IAPWS) has adopted this correlation as an international standard guideline.[36]
Таблица данных
| Жидкость | Температура (° C) | Surface tension, γ |
|---|---|---|
| Уксусная кислота | 20 | 27.60 |
| Acetic acid (45.1%) + Water | 30 | 40.68 |
| Acetic acid (10.0%) + Water | 30 | 54.56 |
| Ацетон | 20 | 23.70 |
| Кровь | 22 | 55.89 |
| Диэтиловый эфир | 20 | 17.00 |
| Этиловый спирт | 20 | 22.27 |
| Ethanol (40%) + Water | 25 | 29.63 |
| Ethanol (11.1%) + Water | 25 | 46.03 |
| Глицерин | 20 | 63.00 |
| п-Hexane | 20 | 18.40 |
| Соляная кислота 17.7 M водный раствор | 20 | 65.95 |
| Изопропанол | 20 | 21.70 |
| Liquid helium II | −273 | 0.37[38] |
| Liquid nitrogen | −196 | 8.85 |
| Жидкий кислород | −182 | 13.2 |
| Меркурий | 15 | 487.00 |
| Метанол | 20 | 22.60 |
| Расплавленный Хлорид серебра | 650 | 163[39] |
| Расплавленный Натрия хлорид/Хлорид кальция (47/53 mole %) | 650 | 139[40] |
| п-Octane | 20 | 21.80 |
| Натрия хлорид 6.0 M водный раствор | 20 | 82.55 |
| Сахароза (55%) + water | 20 | 76.45 |
| Вода | 0 | 75.64 |
| Вода | 25 | 71.97 |
| Вода | 50 | 67.91 |
| Вода | 100 | 58.85 |
| Толуол | 25 | 27.73 |
Gallery of effects
A soap bubble balances surface tension forces against internal пневматический давление.
Surface tension prevents a coin from sinking: the coin is indisputably denser than water, so it must be displacing a volume greater than its own for плавучесть to balance mass.
Смотрите также
- Анти туман
- Капиллярная волна — short waves on a water surface, governed by surface tension and inertia
- Cheerio effect — the tendency for small wettable floating objects to attract one another.
- Сплоченность
- Безразмерные числа
- Дортмундский банк данных — contains experimental temperature-dependent surface tensions
- Electrodipping force
- Электросмачивание
- Electrocapillarity
- Правило Этвёша — a rule for predicting surface tension dependent on temperature
- Труба для жидкости
- Гидростатическое равновесие—the effect of gravity pulling matter into a round shape
- Интерфейс (химия)
- Мениск — surface curvature formed by a liquid in a container
- Меркурий бьется в сердце — a consequence of inhomogeneous surface tension
- Микрофлюидика
- Техника Sessile drop
- Sow-Hsin Chen
- Удельная поверхностная энергия — same as surface tension in isotropic materials.
- Spinning drop method
- Stalagmometric method
- Поверхностное давление
- Наука о поверхности
- Surface tension biomimetics
- Surface tension values
- Поверхностно-активные вещества — substances which reduce surface tension.
- Уравнение Шишковского — Calculating surface tension of aqueous solutions
- Слезы вина — the surface tension induced phenomenon seen on the sides of glasses containing alcoholic beverages.
- Tolman length — leading term in correcting the surface tension for curved surfaces.
- Смачивание и обезвоживание
Примечания
- ^ В ртутный барометр, the upper liquid surface is an interface between the liquid and a vacuum containing some molecules of evaporated liquid.
Рекомендации
- ^ а б c "Surface Tension (Water Properties) – USGS Water Science School". Геологическая служба США. Июль 2015 г.. Получено 6 ноября, 2015.
- ^ а б c Berry, M V (1971). "The molecular mechanism of surface tension" (PDF). Физическое образование. 6: 79-84. Получено 8 июля 2020.
- ^ а б c White, Harvey E. (1948). Modern College Physics. ван Ностранд. ISBN 978-0-442-29401-4.
- ^ Bush, John W. M. (May 2004). "MIT Lecture Notes on Surface Tension, lecture 5" (PDF). Массачусетский Институт Технологий. Получено 1 апреля, 2007.
- ^ Bush, John W. M. (May 2004). "MIT Lecture Notes on Surface Tension, lecture 3" (PDF). Массачусетский Институт Технологий. Получено 1 апреля, 2007.
- ^ Bush, John W. M. (April 2004). "MIT Lecture Notes on Surface Tension, lecture 1" (PDF). Массачусетский Институт Технологий. Получено 1 апреля, 2007.
- ^ "Mechanical definition of surface tension". Массачусетский технологический институт. Получено Dec 16, 2013.
- ^ а б c d е ж грамм час Sears, Francis Weston; Zemanski, Mark W. (1955) University Physics 2nd ed. Эддисон Уэсли
- ^ а б c d е ж грамм час Пьер-Жиль де Жен; Françoise Brochard-Wyart; David Quéré (2002). Capillarity and Wetting Phenomena—Drops, Bubbles, Pearls, Waves. Alex Reisinger. Springer. ISBN 978-0-387-00592-8.
- ^ Батт, Ханс-Юрген; Graf, Karlheinz; Kappl, Michael (2006). Физика и химия интерфейсов. Вайли. п. 9. ISBN 978-3-527-60640-5.
- ^ Aaronson, Scott (March 2005) NP-complete Problems and Physical Reality. Новости ACM SIGACT
- ^ а б c d "Surface Tension by the Ring Method (Du Nouy Method)" (PDF). PHYWE. Получено 2007-09-08.
- ^ а б "Surface tension measurement". Получено 2019-12-31.
- ^ "Surfacants at interfaces" (PDF). lauda.de. Архивировано из оригинал (PDF) на 2007-09-27. Получено 2007-09-08.
- ^ Calvert, James B. "Surface Tension (physics lecture notes)". Денверский университет. Получено 2007-09-08.
- ^ "Sessile Drop Method". Dataphysics. Архивировано из оригинал 8 августа 2007 г.. Получено 2007-09-08.
- ^ Vicente, C.; Yao, W .; Maris, H.; Seidel, G. (2002). "Surface tension of liquid 4He as measured using the vibration modes of a levitated drop". Физический обзор B. 66 (21): 214504. Bibcode:2002PhRvB..66u4504V. Дои:10.1103/PhysRevB.66.214504.
- ^ Zografov, Nikolay (2014). "Droplet oscillations driven by an electric field". Коллоиды и поверхности A: физико-химические и технические аспекты. 460: 351–354. Дои:10.1016/j.colsurfa.2013.12.013.
- ^ Tankovsky, N. (2013). "Electrically Driven Resonant Oscillations of Pendant Hemispherical Liquid Droplet and Possibility to Evaluate the Surface Tension in Real Time". Zeitschrift für Physikalische Chemie. 227 (12). Дои:10.1524/zpch.2013.0420.
- ^ Tankovsky, Nikolay (2011). "Oscillations of a Hanging Liquid Drop, Driven by Interfacial Dielectric Force". Zeitschrift für Physikalische Chemie. 225 (4): 405–411. Дои:10.1524/zpch.2011.0074.
- ^ а б c d Гиббс, Дж. (2002) [1876–1878], "О равновесии неоднородных веществ.", in Bumstead, H.A.; Van Nameeds, R.G. (eds.), The Scientific Papers of J. Willard Gibbs, 1, Woodbridge, CT: Ox Bow Press, pp. 55–354, ISBN 978-0918024770
- ^ а б Ландо; Lifshitz (1980). Course of Theoretical Physics Volume 5: Statistical Physics I (3-е изд.). Пергамон. pp. 517–537.
- ^ Rusanov, A (2005). "Surface thermodynamics revisited". Отчеты по науке о поверхности. 58 (5–8): 111–239. Дои:10.1016/j.surfrep.2005.08.002. ISSN 0167-5729.
- ^ van der Waals, J.D. (1979) [1893], translated by Rowlinson, J.S., "The thermodynamic theory of capillarity under the hypothesis of a continuous variation of density", J. Stat. Phys., 20 (2): 197–200, Bibcode:1979JSP....20..197R, Дои:10.1007/BF01011513
- ^ Cahn, J.W.; Hilliard, J.E. (1958), "Free energy of a nonuniform system. I. Interfacial free energy", J. Chem. Phys., 28 (2): 258–266, Bibcode:1958ЖЧФ..28..258С, Дои:10.1063/1.1744102
- ^ Langer, J.S .; Bar-On, M.; Миллер, Х. (1975), "New computational method in the theory of spinodal decomposition", Phys. Ред. А, 11 (4): 1417–1429, Bibcode:1975ПхРвА..11.1417Л, Дои:10.1103 / PhysRevA.11.1417
- ^ Горбань, А.Н .; Karlin, I. V. (2016), "Beyond Navier–Stokes equations: capillarity of ideal gas", Современная физика (Review article), 58 (1): 70–90, arXiv:1702.00831, Bibcode:2017ConPh..58...70G, Дои:10.1080/00107514.2016.1256123
- ^ а б c d Adam, Neil Kensington (1941). The Physics and Chemistry of Surfaces, 3rd ed. Издательство Оксфордского университета.
- ^ а б "Physical Properties Sources Index: Eötvös Constant". Архивировано из оригинал на 2011-07-06. Получено 2008-11-16.
- ^ Vargaftik, N. B.; Volkov, B. N.; Voljak, L. D. (1983). "International Tables of the Surface Tension of Water" (PDF). Журнал физических и химических справочных данных. 12 (3): 817. Bibcode:1983JPCRD..12..817V. Дои:10.1063/1.555688.
- ^ а б c Moore, Walter J. (1962). Physical Chemistry, 3rd ed. Прентис Холл.
- ^ Ertl, G .; Knözinger, H. and Weitkamp, J. (1997) Handbook of heterogeneous catalysis, Vol. 2, стр. 430. Wiley-VCH, Weinheim. ISBN 3-527-31241-2
- ^ а б International Association for the Properties of Water and Steam (June 2014). "Revised Release on Surface Tension of Ordinary Water Substance".
- ^ Nayar, K. G; Panchanathan, D; McKinley, G. H; Lienhard, J. H (November 2014). "Surface tension of seawater" (PDF). J. Phys. Chem. Ref. Данные. 43 (4): 43103. Bibcode:2014JPCRD..43d3103N. Дои:10.1063/1.4899037. HDL:1721.1/96884.
- ^ Millero, Frank J; Feistel, Rainer; Wright, Daniel G; McDougall, Trevor J (January 2008). "The composition of Standard Seawater and the definition of the Reference-Composition Salinity Scale". Глубоководные исследования, часть I. 55 (1): 50. Bibcode:2008DSRI...55...50M. Дои:10.1016/j.dsr.2007.10.001.
- ^ Guideline on the Surface Tension of Seawater (PDF) (Технический отчет). International Association for the Properties of Water and Steam. October 2019. IAPWS G14-19. Получено 2020-03-26.
- ^ Lange's Handbook of Chemistry (1967) 10th ed. pp 1661–1665 ISBN 0-07-016190-9 (11-е изд.)
- ^ Brouwer, W; Pathria, R. K (1967). "On the Surface Tension of Liquid Helium II". Физический обзор. 163 (1): 200–205. Bibcode:1967PhRv..163..200B. Дои:10.1103/PhysRev.163.200.
- ^ Moser, Z; Gasior, W; Rzyman, K (1982). "Activities and Surface Tension of Liquid AgCl-KCl Solutions". Журнал Электрохимического общества. 129 (3): 502–506. Дои:10.1149/1.2131529.
- ^ Addison, C; Coldrey, J (1960). "Influence of Surface Reactions on the Interface Between Liquid Sodium and Molten Sodium Chloride + Calcium Chloride Mixtures". Труды общества Фарадея. 56: 840–845.
внешняя ссылка
| Викискладе есть медиафайлы по теме Поверхностное натяжение. |
- What is surface tension?
- On surface tension and interesting real-world cases
- Surface Tensions of Various Liquids
- Calculation of temperature-dependent surface tensions for some common components
- Surface tension calculator for aqueous solutions containing the ions H+, NH+
4, Na+, К+, Mg2+, Ca2+, ТАК2−
4, НЕТ−
3, Cl−, CO2−
3, Br− и ОН−. - Т. Проктор Холл (1893) New methods of measuring surface tension in liquids, Философский журнал (series 5, 36: 385–415), link from Библиотека наследия биоразнообразия.
- Стена пузырей (Audio slideshow from the National High Magnetic Field Laboratory explaining cohesion, surface tension and hydrogen bonds)
- C. Pfister: Interface Free Energy. Scholarpedia 2010 (from first principles of statistical mechanics)
- Fundamentals of surface and interfacial tension
- Surface and Interfacial Tension
- "Molten salts mixture surface tension". Журнал химической термодинамики. 3 (2): 259–265. Март 1971 г. Дои:10.1016/S0021-9614(71)80111-8.























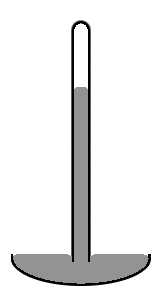






































![{ displaystyle gamma _ { text {w}} = 235,8 left (1 - { frac {T} {T _ { text {C}}}} right) ^ {1.256} left [1-0,625 left (1 - { frac {T} {T _ { text {C}}}} right) right] ~ { text {mN / m}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b65193820b2a29652f19d30a1adecdf0c13c8ea)








