WikiDer > Номограмма
А номограмма (из Греческий νόμος номос, «закон» и γραμμή грамма, "линия"), также называемый номограмма, таблица выравнивания, или же абак, представляет собой графическое вычислительное устройство, двумерную диаграмму, предназначенную для приблизительного графического вычисления математическая функция. Область номографии была изобретена в 1884 году французским инженером. Филбер Морис д'Окань (1862–1938) и широко использовался в течение многих лет для предоставления инженерам быстрых графических расчетов сложных формул с практической точностью. В номограммах используется параллель система координат изобретенный d'Ocagne, а не стандартный Декартовы координаты.
Номограмма состоит из набора из n шкал, по одной для каждой переменной в уравнении. Зная значения n-1 переменных, можно найти значение неизвестной переменной или, зафиксировав значения некоторых переменных, можно изучить взаимосвязь между нефиксированными переменными. Результат получается путем наложения линейки на известные значения на шкалах и считывания неизвестного значения с того места, где оно пересекает шкалу для этой переменной. Виртуальная или нарисованная линия, созданная линейкой, называется индексная строка или же изоплета.
Номограммы процветали в самых разных контекстах на протяжении примерно 75 лет, потому что они позволяли быстро и точно вычислять до эпохи карманных калькуляторов. Результаты номограммы можно получить очень быстро и надежно, просто проведя одну или несколько линий. Пользователь не должен знать, как решать алгебраические уравнения, искать данные в таблицах, использовать логарифмическая линейка, или подставьте числа в уравнения для получения результатов. Пользователю даже не нужно знать основное уравнение, которое представляет номограмма. Кроме того, номограммы, естественно, включают неявные или явные базовые знания в их дизайн. Например, чтобы создать более крупные номограммы для большей точности, номограф обычно включает только разумные диапазоны шкалы, которые представляют интерес для проблемы. Многие номограммы включают другие полезные обозначения, такие как справочные метки и цветные области. Все они служат полезными ориентирами для пользователя.

Как и логарифмическая линейка, номограмма представляет собой графическое аналоговое вычислительное устройство, и, как и линейка, ее точность ограничена точностью, с которой можно рисовать, воспроизводить, просматривать и выравнивать физические отметки. В то время как логарифмическая линейка предназначена для использования в качестве универсального устройства, номограмма предназначена для выполнения конкретных расчетов, а таблицы значений эффективно встроены в конструкцию напольные весы. Номограммы обычно используются в приложениях, где уровень точности, который они предлагают, является достаточным и полезным. В качестве альтернативы, номограмму можно использовать для проверки ответа, полученного в результате другого, более точного, но, возможно, подверженного ошибкам расчета.
Другие типы графических калькуляторов, такие как карты перехвата, трилинейные диаграммы и гексагональные диаграммы иногда называют номограммами. Другие такие примеры включают Диаграмма Смита, графический калькулятор, используемый в электроника и системный анализ, термодинамические диаграммы и тефиграммы, используется для построения вертикальной структуры атмосферы и выполнения расчетов ее устойчивости и влажности. Они не соответствуют строгому определению номограммы как графического калькулятора, решение которого находится с использованием одной или нескольких линейных изоплет.
Описание
Номограмма для уравнения с тремя переменными обычно имеет три шкалы, хотя существуют номограммы, в которых две или даже все три шкалы являются общими. Здесь две шкалы представляют известные значения, а третья - шкала, по которой считывается результат. Простейшее такое уравнение: ты1 + ты2 + ты3 = 0 для трех переменных ты1, ты2 и ты3. Пример номограммы этого типа показан справа, с комментариями, содержащими термины, используемые для описания частей номограммы.
Более сложные уравнения иногда можно выразить как сумму функций трех переменных. Например, номограмма в верхней части этой статьи может быть построена как номограмма в параллельном масштабе, потому что ее можно выразить в виде такой суммы после логарифмирования обеих частей уравнения.
Шкала неизвестной переменной может находиться между двумя другими шкалами или вне их. Известные значения расчета отмечаются на шкалах для этих переменных, и между этими отметками проводится линия. Результат считывается по неизвестной шкале в точке, где линия пересекает эту шкалу. Шкалы включают «деления», чтобы указать точное расположение чисел, и они также могут включать помеченные справочные значения. Эти весы могут быть линейный, логарифмический, или иметь более сложные отношения.
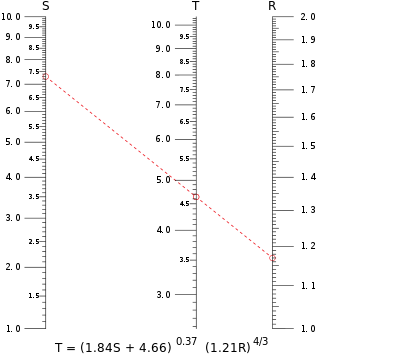
Изоплета образца, показанная красным на номограмме вверху статьи, рассчитывает значение Т когда S = 7,30 и р = 1,17. Изоплета пересекает шкалу для Т чуть менее 4,65; большая цифра, напечатанная на бумаге с высоким разрешением, даст Т = 4,64 с точностью до трех цифр. Обратите внимание, что любая переменная может быть вычислена из значений двух других, функция номограмм, которая особенно полезна для уравнений, в которых переменная не может быть алгебраически изолирована от других переменных.
Прямые шкалы полезны для относительно простых вычислений, но для более сложных вычислений может потребоваться использование простых или сложных изогнутых шкал. Номограммы для более чем трех переменных могут быть построены путем включения сетки шкал для двух переменных или объединения отдельных номограмм меньшего числа переменных в составную номограмму.
Приложения
Номограммы использовались во множестве приложений. Образец включает
- Оригинальное приложение от d'Ocagne, автоматизация сложных вырезать и заполнить расчеты на удаление земли при строительстве национальной железнодорожной системы Франции. Это было важным подтверждением концепции, потому что вычисления нетривиальны, а результаты переводятся в значительную экономию времени, усилий и денег.
- Конструкция каналов, труб и проводов для регулирования расхода воды.
- Работа Лоуренс Хендерсон, в котором номограммы использовались для корреляции многих различных аспектов физиологии крови. Это было первое широкое использование номограмм в Соединенных Штатах, а также первые медицинские номограммы где-либо. Номограммы по-прежнему широко используются в медицинских областях.
- Баллистические расчеты до систем управления огнем, где расчет времени был критичным.
- Расчеты в механическом цеху для преобразования размеров чертежей и выполнения расчетов на основе размеров и свойств материала. Эти номограммы часто включают маркировку стандартных размеров и доступных изготовленных деталей.
- Статистика для сложных расчетов свойств распределений и исследования операций, включая разработку приемочных испытаний для контроля качества.
- Исследование операций для получения результатов в различных задачах оптимизации.
- Химия и химическая инженерия, чтобы инкапсулировать как общие физические отношения, так и эмпирические данные для конкретных соединений.
- Аэронавтика, в которой номограммы десятилетиями использовались в кабинах самолетов всех типов. В качестве средства навигации и управления полетом номограммы были быстрыми, компактными и простыми в использовании калькуляторами.
- Астрономические расчеты, как в орбитальных расчетах после запуска Спутник 1 автор: P.E. Эльясберг.[1]
- Все виды инженерных работ: электрическое проектирование фильтров и линий передачи, механические расчеты напряжений и нагрузок, оптические расчеты и т. Д.
- Военные, где сложные вычисления необходимо производить в полевых условиях быстро и надежно, независимо от электрических устройств.
- Сейсмология, где были разработаны номограммы для оценки землетрясений величина и представить результаты вероятностных сейсмическая опасность анализы[2]
Примеры
Параллельное сопротивление / тонкие линзы

Номограмма ниже выполняет расчет
Эта номограмма интересна тем, что она выполняет полезные нелинейные вычисления с использованием только прямолинейных шкал с одинаковыми градациями. В то время как диагональная линия имеет масштаб раз больше, чем масштабы осей, цифры на нем точно соответствуют числам непосредственно под или слева от него, и, таким образом, его можно легко создать, нарисовав прямую линию по диагонали на листе миллиметровая бумага.
А и B вводятся на горизонтальной и вертикальной шкалах, а результат считывается на диагональной шкале. Будучи пропорциональным гармоническое среднее из А и B, эта формула имеет несколько применений. Например, это формула параллельного сопротивления в электроника, а уравнение тонкой линзы в оптика.
В примере красная линия показывает, что параллельные резисторы 56 и 42Ом имеют суммарное сопротивление 24 Ом. Это также демонстрирует, что объект на расстоянии 56 см от линза чей фокусное расстояние 24 см образует реальное изображение на расстоянии 42 см.
Расчет критерия хи-квадрат

Номограмму ниже можно использовать для приблизительного вычисления некоторых значений, необходимых при выполнении знакомого статистического теста, Критерий хи-квадрат Пирсона. Эта номограмма демонстрирует использование изогнутых шкал с неравномерно расположенными градуировками.
Соответствующее выражение
Шкала вверху используется для пяти различных диапазонов наблюдаемых значений: A, B, C, D и E. Наблюдаемое значение находится в одном из этих диапазонов, а метка, используемая на этой шкале, находится непосредственно над ним. Затем в зависимости от диапазона выбирается изогнутая шкала, используемая для ожидаемого значения. Например, для наблюдаемого значения 9 будет использоваться отметка над 9 в диапазоне A, а изогнутая шкала A будет использоваться для ожидаемого значения. Наблюдаемое значение 81 будет использовать отметку выше 81 в диапазоне E, а кривая шкала E будет использоваться для ожидаемого значения. Это позволяет объединить пять различных номограмм в единую диаграмму.
Таким образом, синяя линия демонстрирует вычисление
- (9 − 5)2/ 5 = 3.2
а красная линия показывает вычисление
- (81 − 70)2 / 70 = 1.7
При выполнении теста Поправка Йетса на непрерывность часто применяется, и просто требует вычитания 0,5 из наблюдаемых значений. Номограмма для выполнения теста с поправкой Йейтса может быть построена просто путем сдвига каждой «наблюдаемой» шкалы на половину единицы влево, так что деления 1,0, 2,0, 3,0, ... помещаются там, где значения 0,5, 1,5, 2,5 , ... появляются на данной диаграмме.
Оценка пищевых рисков

Хотя номограммы представляют собой математические отношения, не все они получены математическим путем. Следующий был разработан графически для достижения соответствующих конечных результатов, которые можно было бы легко определить по продукту их взаимоотношений в субъективных единицах, а не численно. Использование непараллельных осей позволило включить в модель нелинейные зависимости.
Цифры в квадратных ячейках обозначают оси, требующие ввода после соответствующей оценки.
Пара номограмм в верхней части изображения определяет вероятность возникновения и доступность, которые затем включаются в нижнюю многоступенчатую номограмму.
Строки 8 и 10 являются «связующими линиями» или «линиями поворота» и используются для перехода между этапами составной номограммы.
Последняя пара параллельных логарифмических шкал (12) не являются номограммами как таковые, а являются шкалами отсчета для перевода оценки риска (11, от отдаленного до чрезвычайно высокого) в частоту выборки для рассмотрения аспектов безопасности и других аспектов «защиты потребителей» соответственно. . На этом этапе требуется политическая «поддержка», уравновешивающая стоимость и риск. В примере используется трехлетняя минимальная частота для каждого, хотя крайняя граница шкалы высокого риска отличается для двух аспектов, давая разную частоту для двух, но оба при условии общей минимальной выборки каждого пищевого продукта по крайней мере для всех аспектов. раз в три года.
Этот оценка рисков номограмма была разработана Служба общественных аналитиков Великобритании при финансировании из Агентство по пищевым стандартам Великобритании для использования в качестве инструмента для определения соответствующей частоты отбора проб и анализа пищевых продуктов для официальных целей контроля пищевых продуктов, предназначенного для использования для оценки всех потенциальных проблем со всеми пищевыми продуктами, хотя еще не принят.
Оценка размера выборки
Эту номограмму можно использовать для оценки требований к размеру выборки для статистического анализа. Он использует четыре параметра: α (фиксировано), размер эффекта (ρ или же δ), статистическая мощность и количество наблюдений N (две шкалы для α = 0,05 (либеральный) или 0,01 (консервативный)).
Предполагаемый размер эффекта в популяции может быть выражен как коэффициент корреляции (ρ) или нормализованная разница в средних (δ) для Т-тест. Нормализованная разница равна абсолютному значению разницы между двумя средними значениями совокупности (μ₁ − μ₂), деленное на объединенное стандартное отклонение (s).
Желаемая статистическая мощность оценивается как 1 - β, куда β равна вероятности совершения ошибки типа II. А тип II ошибка не может отклонить статистическую нулевую гипотезу (т. е. ρ или же δ равен нулю), тогда как на самом деле нулевая гипотеза ложна для популяции и должна быть отклонена. Коэн (1977)[3] рекомендует использовать мощность равную 0,80 или 80%, для β = 0.20 .
Размер выборки или необходимое количество случаев указывается для двух стандартных уровней статистической значимости (α = 0,01 или 0,05). Значение α - вероятность ошибки типа I. А тип I ошибка отвергает статистическую нулевую гипотезу (т. е. утверждает, что либо ρ или же δ равен нулю), тогда как на самом деле является истина (значение является ноль) в популяции и должен нет быть отклоненным. Наиболее часто используемые значения α - 0,05 или 0,01.
Чтобы найти требования к размеру выборки для данного статистического анализа, оцените размер эффекта, ожидаемого в генеральной совокупности (ρ или же δ) на левой оси выберите желаемый уровень мощности на правой оси и проведите линию между двумя значениями.
Если линия пересекается с α = 0,05 или α = 0,01 на средней оси будет указан размер выборки, необходимый для достижения статистической значимости α менее 0,05 или 0,01 соответственно (для ранее заданных параметров).
Например, если оценить корреляцию населения (ρ) равным 0,30 и желает статистической мощности равной 0,80, чтобы затем получить уровень значимости α менее 0,05, размер выборки будет N = 70 случаев с округлением в большую сторону (точнее, примерно 68 случаев с использованием интерполяции).
Другие быстрые номограммы
Используя линейку, можно легко прочитать недостающий член закон синуса или корни квадратичный и кубический уравнение.[4]
Смотрите также
- Картограмма
- Система координат
- Тринадцатая проблема Гильберта
- Лог-лог-график
- Полугодовой график
- Диаграмма Смита
Рекомендации
Эта статья включает в себя список общих Рекомендации, но он остается в основном непроверенным, потому что ему не хватает соответствующих встроенные цитаты. (Ноябрь 2013) (Узнайте, как и когда удалить этот шаблон сообщения) |
- ^ Ю.А. Мозжорин Воспоминания В архиве 2007-10-18 на Wayback Machine на сайте Российского государственного архива научно-технической документации
- ^ Дуглас, Джон; Данчу, Лаурентиу (2019-11-08). «Номограмма для объяснения вероятностной сейсмической опасности». Журнал сейсмологии: 671. Bibcode:2019JSeis.tmp..671D. Дои:10.1007 / s10950-019-09885-4. ISSN 1573–157X.
- ^ Коэн, Дж. (1977). Статистический анализ мощности для поведенческих наук, 2-й. изд. Сан-Диего, Калифорния: Academic Press
- ^ Шалкаи, Иштван; Балинт, Роланд (28 декабря 2017 г.). «Номограммы для квадратных и кубических уравнений (на венгерском языке)» (PDF). Haladvány Kiadvány. 2017.
дальнейшее чтение
- Д.П. Адамс, Номография: теория и применение, (Книги Archon) 1964.
- Х. Дж. Оллкок, Дж. Реджинальд Джонс и Дж. Г.Л. Мишель, Номограмма. Теория и практическое построение вычислительных схем, 5-е изд. (Лондон: Sir Isaac Pitman & Sons, Ltd.) 1963.
- С. Бродестский, Первый курс по номографии, (Лондон, Дж. Белл и сыновья) 1920.
- Д.С. Дэвис, Эмпирические уравнения и номография(Нью-Йорк: McGraw-Hill Book Co.) 1943 г.
- М. д'Окань: Traité de Nomographie, (Готье-Виллар, Париж) 1899 г.
- М. д'Окань: (1900) Sur la résolution nomographique de l'équation du septième degré. Comptes rendus (Париж), 131, 522–524.
- Р.Д. Дуглас, Д.П. Адамс, Элементы номографии, (Нью-Йорк: McGraw-Hill) 1947.
- R.P. Hoelscher и др., Графические средства в инженерных вычислениях, (Нью-Йорк: Макгроу-Хилл) 1952.
- Л. Иван Эпштейн, Номография, (Нью-Йорк: издательство Interscience) 1958.
- Л. Х. Джонсон, Номография и эмпирические уравнения, (Нью-Йорк: Джон Вили и сыновья) 1952.
- М. Каттан и Дж. Мараско. (2010) Что такое настоящая номограмма?, Семинары по онкологии, 37 (1), 23–26.
- В КАЧЕСТВЕ. Левенс, Номография, 2-е изд. (Нью-Йорк: John Wiley & Sons, Inc.) 1959.
- F.T. Мавис, Построение номографических карт, (Скрэнтон, Международный учебник) 1939.
- Э. Отто, Номография, (Нью-Йорк: компания Macmillan) 1963.
- Х.А. Evesham История и развитие номографии, (Бостон: Docent Press) 2010. ISBN 9781456479626
- T.H. Gronwall, R. Doerfler, A. Gluchoff и S. Guthery, Расчет кривых: математика, история и эстетическая привлекательность номографической работы Т. Х. Гронуолла, (Бостон: Docent Press) 2012. ISBN 9780983700432
внешняя ссылка
| Викискладе есть медиафайлы по теме Номограммы. |
| Искать номограмма в Викисловаре, бесплатном словаре. |
- Вайсштейн, Эрик В. «Номограмма». MathWorld.
- Искусство номографии описывает дизайн номограмм с использованием геометрии, определителей и преобразований.
- Утраченное искусство номографии - это статья в математическом журнале, посвященная номографии.
- Номограммы для варгеймов но также представляет общий интерес.
- PyNomo - ПО с открытым кодом для построения номограмм.
- Java-апплет для построения простых номограмм.
- Номограммы для визуализации отношений между тремя переменными - видео и слайды приглашенного выступления Джонатана Ружье для useR! 2011.