WikiDer > Выпрямленный усеченный октаэдр
| Выпрямленный усеченный октаэдр | |
|---|---|
 | |
| Символ Шлефли | rt {3,4} |
| Обозначение Конвея | atO |
| Лица | 38: 24 { }∨() 6 {4} 8 {6} |
| Края | 72 |
| Вершины | 12+24 |
| Группа симметрии | Очас, [4,3], (* 432) порядок 48 |
| Группа вращения | О, [4,3]+, (432), заказ 24 |
| Двойной многогранник | Присоединенный усеченный октаэдр |
| Характеристики | выпуклый |
 Сеть | |
В выпрямленный усеченный октаэдр это многогранник, построенный как исправленный усеченный октаэдр. Имеет 38 лиц: 24 равнобедренные треугольники, 6 квадраты, и 8 шестиугольники.
Топологически квадраты, соответствующие вершинам октаэдра, всегда правильны, хотя шестиугольники, имея равные длины ребер, не имеют одинаковой длины ребер с квадратами, имеют разные, но чередующиеся углы, в результате чего треугольники равнобедренный вместо.
Связанные многогранники
В выпрямленный усеченный октаэдр можно увидеть в последовательности исправление и усечение операции из октаэдр. Дальнейшее усечение и чередование создает еще два многогранника:
| Имя | Усеченный октаэдр | Исправленный усеченный октаэдр | Усеченный исправленный усеченный октаэдр | Курносый исправленный усеченный октаэдр |
|---|---|---|---|---|
| Coxeter | к | rtO | trtO | srtO |
| Конвей | atO | btO | stO | |
| Изображение |  |  | 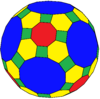 |  |
| Конвей | dtO = kC | jtO | mtO | mtO |
| Двойной |  |  |  |  |
Смотрите также
- Выпрямленный усеченный тетраэдр
- Выпрямленный усеченный куб
- Выпрямленный усеченный додекаэдр
- Исправленный усеченный икосаэдр
Рекомендации
- Coxeter Правильные многогранники, Третье издание, (1973), Дуврское издание, ISBN 0-486-61480-8 (стр. 145–154 Глава 8: Усечение)
- Джон Х. Конвей, Хайди Берджель, Хаим Гудман-Штрасс, Симметрии вещей 2008, ISBN 978-1-56881-220-5
внешняя ссылка
- Переводчик Джорджа Харта Конвея: порождает многогранники в VRML, принимая обозначение Конвея в качестве входных данных
| Этот многогранник-связанная статья является заглушка. Вы можете помочь Википедии расширяя это. |