WikiDer > Полунеявный метод Эйлера
В математике полунеявный метод Эйлера, также называемый симплектический Эйлер, полуявный Эйлер, Эйлер – Кромер, и Ньютон – Стёрмер – Верле (NSV), является модификацией Метод Эйлера для решения Уравнения Гамильтона, система обыкновенные дифференциальные уравнения что возникает в классическая механика. Это симплектический интегратор и, следовательно, он дает лучшие результаты, чем стандартный метод Эйлера.
Параметр
Полунеявный метод Эйлера можно применить к паре дифференциальные уравнения формы
куда ж и грамм даны функции. Здесь, Икс и v могут быть скалярами или векторами. Уравнения движения в Гамильтонова механика принимают этот вид, если гамильтониан имеет вид
Дифференциальные уравнения решаются с начальным условием
Метод
Полунеявный метод Эйлера дает приближенное дискретный решение путем итерации
где Δт это временной шаг и тп = т0 + пΔт время после п шаги.
Отличие от стандартного метода Эйлера состоит в том, что полунеявный метод Эйлера использует vп+1 в уравнении для Иксп+1, а метод Эйлера использует vп.
Применяя метод с отрицательным шагом по времени к вычислению из и перестановка приводит ко второму варианту полунеявного метода Эйлера
который имеет аналогичные свойства.
Полунеявный Эйлер - это интегратор первого порядка, как и стандартный метод Эйлера. Это означает, что он совершает глобальную ошибку порядка Δt. Однако полунеявный метод Эйлера - это симплектический интегратор, в отличие от стандартного метода. Как следствие, полунеявный метод Эйлера почти сохраняет энергию (когда гамильтониан не зависит от времени). Часто энергия неуклонно увеличивается когда применяется стандартный метод Эйлера, что делает его гораздо менее точным.
Чередование двух вариантов полунеявного метода Эйлера приводит в одном упрощении к методу Штёрмера-Интеграция Верле и в несколько ином упрощении чехарда интеграции, увеличивая как порядок ошибки, так и порядок сохранения энергии.[1]
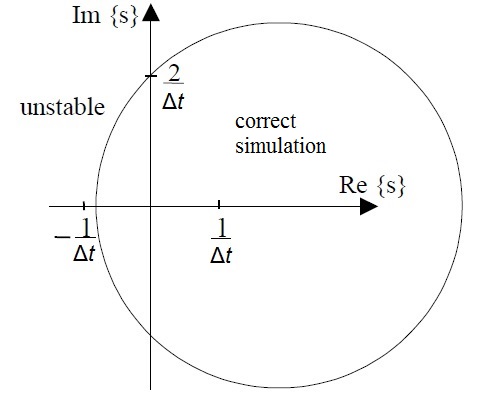
Область устойчивости полунеявного метода была представлена Ниираненом.[2] хотя полунеявный Эйлер ошибочно был назван в своей статье симметричным Эйлером. Полунеявный метод моделирует смоделированную систему правильно, если комплексные корни характеристического уравнения находятся внутри круга, показанного ниже. Для реальных корней область устойчивости выходит за пределы круга, для которого критерий
Как видно, полунеявный метод может правильно моделировать как стабильные системы, корни которых находятся в левой полуплоскости, так и нестабильные системы, корни которых находятся в правой полуплоскости. Это явное преимущество перед прямым (стандартным) Эйлером и обратным Эйлером. Прямой Эйлер имеет тенденцию иметь меньшее затухание, чем реальная система, когда отрицательные действительные части корней приближаются к мнимой оси, а обратный Эйлер может показать, что система стабильна, даже когда корни находятся в правой полуплоскости.
Пример
Движение весна удовлетворение Закон Гука дан кем-то
Полунеявный Эйлер для этого уравнения равен
Подстановка во втором уравнении с выражением, заданным первым уравнением, итерация может быть выражена в следующей матричной форме
и поскольку определитель матрицы равен 1, преобразование сохраняет площадь.
Итерация сохраняет модифицированный функционал энергии точно, приводя к устойчивым периодическим орбитам (для достаточно малого размера шага), отклоняющимся на с точных орбит. Точная круговая частота увеличивается в численном приближении в .
Рекомендации
- ^ Хайрер, Эрнст; Любич, Кристиан; Ваннер, Герхард (2003). «Геометрическое численное интегрирование, иллюстрированное методом Штёрмера / Верле». Acta Numerica. 12: 399–450. CiteSeerX 10.1.1.7.7106. Дои:10.1017 / S0962492902000144.
- ^ Нииранен, Йоуко: Быстрый и точный симметричный алгоритм Эйлера для электромеханического моделирования Труды Electrimacs'99, 14–16 сентября 1999 г. Лиссабон, Португалия, Vol. 1, страницы 71 - 78.
- Джордано, Николас Дж .; Хисао Наканиси (июль 2005 г.). Вычислительная физика (2-е изд.). Бенджамин Каммингс. ISBN 0-13-146990-8.
- Макдональд, Джеймс. «Метод Эйлера-Кромера». Университет Делавэра. Получено 2013-04-11.
- Веселый, Франц Дж. (2001). Вычислительная физика: введение (2-е изд.). Springer. стр.117. ISBN 978-0-306-46631-1.




![egin {align}
v_ {n + 1} & = v_n + g (t_n, x_n), дельта t [0.3em]
x_ {n + 1} & = x_n + f (t_n, v_ {n + 1}), дельта t
конец {выровнять}](https://wikimedia.org/api/rest_v1/media/math/render/svg/96b091ba914ac916145d3b4d9361fd16d0842531)


![{начало {выровнено} x _ {{n + 1}} & = x_ {n} + f (t_ {n}, v_ {n}), Delta t [0.3em] v _ {{n + 1}} & = v_ {n} + g (t_ {n}, x _ {{n + 1}}), дельта склонение {выровнено}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5345b72f06cf73c459fa753eb60f46b693f1dfbf)

![egin {align}
frac {dx} {dt} & = v (t) [0.2em]
гидроразрыв {dv} {dt} & = -frac {k} {m}, x = -omega ^ 2, x.
конец {выровнять}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1b4ad4717bd1a3de6047f098be4c68688433ee9)
![egin {align}
v_ {n + 1} & = v_n - omega ^ 2, x_n, Delta t [0.2em]
x_ {n + 1} & = x_n + v_ {n + 1}, Дельта t.
конец {выровнять}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc8125ba24c3d6f1c7490320f3dafdc3f2a175e9)





