WikiDer > Твердая геометрия
Эта статья нужны дополнительные цитаты для проверка. (Май 2014 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |

В математика, сплошная геометрия традиционное название геометрия из трехмерное евклидово пространство[1] (т.е. 3D геометрия).
Стереометрия имеет дело с измерения из тома различных твердые фигуры (трехмерные фигуры), в том числе пирамиды, призмы и другие многогранники; цилиндры; шишки; усеченные конусы; и мячи ограничен сферы.[2]
История
В Пифагорейцы занимался обычные твердые тела, но пирамида, призма, конус и цилиндр не изучались до Платоники. Евдокс установили свои размеры, доказав, что пирамида и конус имеют одну треть объема призмы и цилиндра на одном основании и на одинаковой высоте. Вероятно, он был также изобретателем доказательства того, что объем, заключенный в сфере, пропорционален кубу ее радиус.[3]
Темы
Основные темы твердотельной геометрии и стереометрии включают:
- заболеваемость из самолеты и линии
- двугранный угол и телесный угол
- в куб, кубовид, параллелепипед
- в тетраэдр и другие пирамиды
- призмы
- октаэдр, додекаэдр, икосаэдр
- шишки и цилиндры
- в сфера
- Другой квадрики: сфероид, эллипсоид, параболоид и гиперболоиды.
Дополнительные темы включают:
- проективная геометрия трех измерений (что приводит к доказательству Теорема дезарга с помощью дополнительного измерения)
- дальше многогранники
- начертательная геометрия.
Твердые фигуры
В то время как сфера это поверхность мяч, иногда бывает неоднозначно, относится ли этот термин к поверхности фигуры или к заключенному в ней объему, особенно для цилиндр. В следующей таблице представлены основные типы фигур, которые составляют или определяют объем.
| Фигура | Определения | Изображений | |
|---|---|---|---|
| Параллелепипед |
| 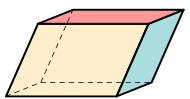 | |
| Ромбоэдр |
| 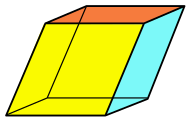 | |
| Кубоид |
|  | |
| Многогранник | Плоский многоугольный лица, прямой края и острые углы или вершины | ||
| Равномерный многогранник | Правильные многоугольники в качестве лица и является вершинно-транзитивный (т.е. существует изометрия отображение любой вершины на любую другую) | ||
| Призма | А многогранник включая п-сторонний многоугольный основание, вторая база, которая является переведено копия (жестко перемещенная без вращения) первой, и п Другой лица (обязательно все параллелограммы) присоединение соответствующие стороны из двух баз | 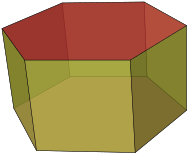 | |
| Конус | Плавно сужается от плоского основания (часто, но не обязательно круглого) к точке, называемой вершина или же вершина | ||
| Цилиндр | Прямые параллельные стороны и круглое или овальное сечение | ||
| Эллипсоид | Поверхность, которая может быть получена из сфера деформируя его с помощью направленного масштабированиеили, в более общем смысле, аффинное преобразование | ||
| Лимон | А линза (или менее половины дуги окружности), повернутой вокруг оси, проходящей через концы линзы (или дуги)[6] |  | |
| Гиперболоид | А поверхность который создается вращением гипербола вокруг одного из главные оси |  |
Методы
В твердотельной геометрии используются различные методы и инструменты. Среди них, аналитическая геометрия и вектор методы имеют большое влияние, позволяя систематически использовать линейные уравнения и матрица алгебра, которые важны для более высоких измерений.
Приложения
Основное применение твердотельной геометрии и стереометрии находится в 3D компьютерная графика.
Смотрите также
- Области мяча
- Евклидова геометрия
- Измерение
- Точка
- Планиметрия
- Форма
- Списки фигур
- Поверхность
- Площадь поверхности
- Архимед
Примечания
- ^ Британский путеводитель по геометрии, Britannica Educational Publishing, 2010, стр. 67–68.
- ^ Киселев 2008.
- ^ Перефразировано и частично взято из 1911 Британская энциклопедия.
- ^ Робертсон, Стюарт Александр (1984). Многогранники и симметрия. Издательство Кембриджского университета. п.75. ISBN 9780521277396.
- ^ Дюпюи, Натан Феллоуз (1893). Элементы синтетической твердотельной геометрии. Макмиллан. п.53. Получено 1 декабря, 2018.
- ^ Вайсштейн, Эрик В. "Лимон". Вольфрам MathWorld. Получено 2019-11-04.
Рекомендации
- Киселев, А. П. (2008). Геометрия. Книга II. Стереометрия. Перевод Гивенталя, Александра. Сумиздат.CS1 maint: ref = harv (связь)








